
- •1.Определение цос. Физические сигналы и методы их обработки
- •2.Дискретизация и квантование аналоговых сигналов.
- •3.Класификация сигналов Классификация сигналов
- •4.Энергетические характеристики сигналов
- •5.Расположение в ряд Фурье
- •6.Преобразование Фурье
- •7.Дискретное преобразование Фурье
- •8.Основные свойства дпф
- •9. Утечка дпф. Спектральные функции
- •11. Дискретное косинусное преобразование. Преобразование Уолша
- •12. Вейвлет-преобразование
- •17.Свертка
- •18.Цифровые фильтры
- •[Править]Преимущества и недостатки
- •[Править]Недостатки
- •[Править]Виды цифровых фильтров [править]ких-фильтры
- •[Править]бих-фильтры
- •[Править]Способы реализации цифровых фильтров
- •Типы фильтров
12. Вейвлет-преобразование
Вейвлет-преобразование (англ. Wavelet transform) — интегральное преобразование, которое представляет собой свертку вейвлет-функции с сигналом.
Cпособ преобразования функции (или сигнала) в форму, которая или делает некоторые величины исходного сигнала более поддающимися изучению, или позволяет сжать исходный набор данных. Вейвлетное преобразование сигналов является обобщением спектрального анализа. Термин (англ. wavelet) в переводе с английского означает "маленькая волна". Вейвлеты — это обобщённое название математических функций определенной формы, которые локальны во времени и по частоте и в которых все функции получаются из одной базовой, изменяя её (сдвигая, растягивая).
Требования к вейвлетам
Для осуществления вейвлет-преобразования вейвлет-функции должны удовлетворять следующим критериям[1]:
1. Вейвлет должен обладать конечной энергией:
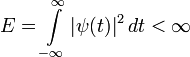
2.
Если ![]() фурье-преобразование для
фурье-преобразование для ![]() ,
то есть
,
то есть
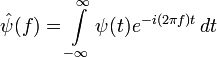
тогда должно выполняться следующее условие:
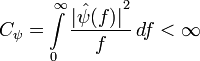
Это
условие называется условием допустимости,
и из него следует что вейвлет при нулевой
частотной компоненте должен удовлетворять
условию ![]() или,
в другом случае, вейвлет
должен
иметь среднее равное нулю.
или,
в другом случае, вейвлет
должен
иметь среднее равное нулю.
3. Дополнительный критерий предъявляется для комплексных вейвлетов, а именно, что для них Фурье-преобразование должно быть одновременно вещественным и должно убывать для отрицательных частот.
4. Локализация: вейвлет должен быть непрерывным, интегрируемым, иметь компактный носитель и быть локализованным как во времени (в пространстве), так и по частоте. Если вейвлет в пространстве сужается, то его средняя частота повышается, спектр вейвлета перемещается в область более высоких частот и расширяется. Этот процесс должен быть линейным – сужение вейвлета вдвое должно повышать его среднюю частоту и ширину спектра также вдвое.
[править]Свойства вейвлет преобразования
1. Линейность
![]()
2. Инвариантность относительно сдвига
![]()
Сдвиг сигнала во времени на t0 приводит к сдвигу вейвлет-спектра также на t0.
3. Инвариантность относительно масштабирования
![]()
Растяжение (сжатие) сигнала приводит к сжатию (растяжению) вейвлет-спектра сигнала.
4. Дифференцирование
![]()

Отсюда следует, что безразлично, дифференцировать ли функцию или анализирующий вейвлет. Если анализирующий вейвлет задан формулой, то это может быть очень полезным для анализа сигналов. Это свойство особенно полезно, если сигнал задан дискретным рядом.
[править]Непрерывное вейвлет-преобразование
Вейвлет преобразование для непрерывного сигнала относительно вейвлет функции определяется следующим образом[1]:

где ![]() означает
комплексное сопряжение для
означает
комплексное сопряжение для ![]() ,
параметр
,
параметр ![]() соответствует
временному сдвигу, и называется параметром
положения, параметр
соответствует
временному сдвигу, и называется параметром
положения, параметр ![]() задает
масштабирование и называется параметром
растяжения.
задает
масштабирование и называется параметром
растяжения.
![]() —
весовая
функция.
—
весовая
функция.
Мы можем определить нормированную функцию следующим образом

что означает временной сдвиг на b и масштабирование по времени на a. Тогда формула вейлет-преобразования изменится на

Исходный сигнал может быть восстановлен по формуле обратного преобразования
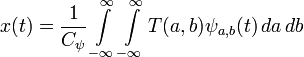
[править]Дискретное вейвлет-преобразование
В дискретном случае, параметры масштабирования a и сдвига b представлены дискретными величинами:
![]() и
и ![]()
Тогда анализирующий вейвлет имеет следующий вид:
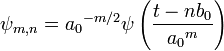
где m и n — целые числа.
В таком случае для непрерывного сигнала дискретное вейвлет-преобразование и его обратное преобразование запишутся следующими формулами:
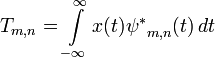
Величины ![]() также
известны как вейвлет-коэффициенты.
также
известны как вейвлет-коэффициенты.
![]()
![]() есть
постоянная нормировки.
есть
постоянная нормировки.
[править]Графическое представление

![]()
Временное и спектральное представления WAVE-вейвлета
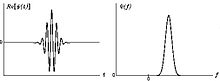
Временное и спектральное представления вейвлета Морле
[править]Применение
Вейвлет-преобразование широко используется для анализа сигналов. Помимо этого, оно находит большое применение в области сжатия данных. В дискретном вейвлет-преобразовании наиболее значимая информация в сигнале содержится при высоких амплитудах, а менее полезная — при низких. Сжатие данных может быть получено за счет отбрасывания низких амплитуд. Вейвлет-преобразование позволяет получить высокое соотношение сжатия в сочетании с хорошим качеством восстановленного сигнала. Вейвлет-преобразование было выбрано для стандартов сжатия изображений JPEG2000 и ICER. Однако, при малых сжатиях вейвлет-преобразование уступает по качеству в сравнении соконным Фурье-преобразованием, которое лежит в основе стандарта JPEG.
Выбор конкретного вида и типа вейвлетов во многом зависит от анализируемых сигналов и задач анализа. Для получения оптимальных алгоритмов преобразования разработаны определенные критерии, но их еще нельзя считать окончательными, т.к. они являются внутренними по отношению к самим алгоритмам преобразования и, как правило, не учитывают внешних критериев, связанных с сигналами и целями их преобразований. Отсюда следует, что при практическом использовании вейвлетов необходимо уделять достаточное внимание проверке их работоспособности и эффективности для поставленных целей по сравнению с известными методами обработки и анализа.
[править]Примечания
Достоинства:
Вейвлетные преобразования обладают всеми достоинствами преобразований Фурье.
Вейвлетные базисы могут быть хорошо локализованными как по частоте, так и по времени. При выделении в сигналах хорошо локализованных разномасштабных процессов можно рассматривать только те масштабные уровни разложения, которые представляют интерес.
Базисные вейвлеты могут реализоваться функциями различной гладкости.
Недостатки:
Можно выделить один недостаток, это относительная сложность преобразования.
13. z-преобразование
Z-преобразованием (преобразованием Лорана)
называют свёртывание исходного сигнала,
заданного последовательностью вещественных
чисел во
временно́й области, в аналитическую
функцию комплексной частоты.
Если сигнал представляет импульсную
характеристику линейной
системы,
то коэффициенты Z-преобразования
показывают отклик системы на комплексные
экспоненты ![]() ,
то есть на гармонические осцилляции с
различными частотами и скоростями
нарастания/затухания.
Определение
,
то есть на гармонические осцилляции с
различными частотами и скоростями
нарастания/затухания.
Определение
Z-преобразование, как и многие интегральные преобразования, может быть задано как одностороннее и двустороннее
[править]Двустороннее Z-преобразование
Двустороннее
Z-преобразование ![]() дискретного
временного сигнала
дискретного
временного сигнала ![]() задаётся
как:
задаётся
как:
![]()
где
—
целое, ![]() —
комплексное число.
—
комплексное число.
![]()
где ![]() —
амплитуда, а
—
амплитуда, а ![]() —
угловая частота (в радианах на
отсчёт)
—
угловая частота (в радианах на
отсчёт)
[править]Одностороннее Z-преобразование
В
случаях, когда
определена
только для ![]() ,
одностороннее Z-преобразование задаётся
как:
,
одностороннее Z-преобразование задаётся
как:
![]()
[править]Обратное Z-преобразование
Обратное Z-преобразование определяется, например, так:

где ![]() —
контур, охватывающий область сходимости
.
Контур должен содержать все вычеты
.
—
контур, охватывающий область сходимости
.
Контур должен содержать все вычеты
.
Положив
в предыдущей формуле ![]() ,
получим эквивалентное определение:
,
получим эквивалентное определение: 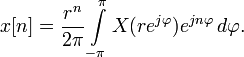
[править]Область сходимости
Область сходимости ![]() представляет
собой некоторое множество точек на
комплексной плоскости, в которых
выполнено условие:
представляет
собой некоторое множество точек на
комплексной плоскости, в которых
выполнено условие:

то есть сумма по членам преобразования является конечной.
[править]Пример 1 (без области сходимости)
Пусть ![]() .
Раскрывая
на
интервале
.
Раскрывая
на
интервале ![]() ,
получаем
,
получаем
![]()
Смотрим на сумму:
![]()
Поэтому, не существует таких значений , которые бы удовлетворяли условию сходимости.
[править]Таблица некоторых Z-преобразований
Обозначения:
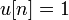 для
,
для
, 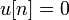 для
для 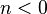 ;
;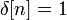 для
для  ,
иначе
,
иначе  .
.
-
Сигнал,
Z-преобразование,
Область сходимости
1



2


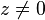
3
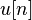

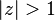
4

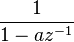

5
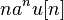
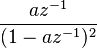
6


7
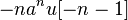
8


9


10

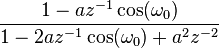
11
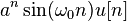

14. Случайные процессы
Случа́йный проце́сс (случайная функция) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты. Другое определение: Случайным называется процесс u(t), мгновенные значения которого являются случайными величинами. Определение
Пусть
дано вероятностное
пространство ![]() .
Параметризованное семейство
.
Параметризованное семейство ![]() случайных
величин
случайных
величин
![]() ,
,
где произвольное множество, называется случайной функцией.
[править]Терминология
Если
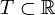 ,
то параметр
,
то параметр 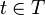 может
интерпретироваться как время.
Тогда случайная функция
может
интерпретироваться как время.
Тогда случайная функция  называется
случайным процессом. Если
множество
дискретно,
например
называется
случайным процессом. Если
множество
дискретно,
например  ,
то такой случайный процесс
называется случа́йной
после́довательностью.
,
то такой случайный процесс
называется случа́йной
после́довательностью.
Если
 ,
где
,
где 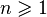 ,
то параметр
может
интерпретироваться как точка в
пространстве, и тогда случайную функцию
называют случа́йным
по́лем.
,
то параметр
может
интерпретироваться как точка в
пространстве, и тогда случайную функцию
называют случа́йным
по́лем.
Данная классификация нестрогая. В частности, термин «случайный процесс» часто используется как безусловный синоним термина «случайная функция».
[править]Классификация
Случайный процесс X(t) называется процессом дискретным во времени, если система, в которой он протекает, меняет свои состояния только в моменты времени t1, t2,…, число которых конечно или счетно. Случайный процесс называется процессом с непрерывным временем, если переход из состояния в состояние может происходить в любой момент времени.
Случайный процесс называется процессом с непрерывными состояниями, если значением случайного процесса является непрерывная случайная величина. Случайный процесс называется случайным процессом с дискретными состояниями, если значением случайного процесса является дискретная случайная величина:
Случайный процесс называется стационарным, если все многомерные законы распределения зависят только от взаимного расположения моментов времени
 ,
но не от самих значений этих величин.
Другими словами, случайный процесс
называется стационарным,
если его вероятностные закономерности
неизменны во времени. В противном
случае, он называется нестационарным.
,
но не от самих значений этих величин.
Другими словами, случайный процесс
называется стационарным,
если его вероятностные закономерности
неизменны во времени. В противном
случае, он называется нестационарным.Случайная функция называется стационарной в широком смысле, если её математическое ожидание и дисперсия постоянны, а АКФ зависит только от разности моментов времени, для которых взяты ординаты случайной функции. Понятие ввёл А. Я. Хинчин.
Случайный процесс называется процессом со стационарными приращениями определенного порядка, если вероятностные закономерности такого приращения неизменны во времени. Такие процессы были рассмотреныЯгломом [1].
Если ординаты случайной функции подчиняются нормальному закону распределения, то и сама функция называется нормальной.
Случайные функции, закон распределения ординат которых в будущий момент времени полностью определяется значением ординаты процесса в настоящий момент времени и не зависит от значений ординат процесса в предыдущие моменты времени, называются марковскими.
Случайный процесс называется процессом с независимыми приращениями, если для любого набора
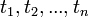 ,
где
,
где  ,
а
,
а  , случайные
величины
, случайные
величины  ,
,  ,
, 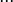 ,
,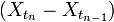 независимы.
независимы.Если при определении моментных функций стационарного случайного процесса операцию усреднения по статистическому ансамблю можно заменить усреднением по времени, то такой стационарный случайный процесс называется эргодическим.
Среди случайных процессов выделяют импульсные случайные процессы.
[править]Траектория случайного процесса
Пусть
дан случайный процесс
.
Тогда для каждого фиксированного
![]() —
случайная величина, называемая сечением.
Если фиксирован элементарный
исход
—
случайная величина, называемая сечением.
Если фиксирован элементарный
исход ![]() ,
то
,
то ![]() —
детерминистическая функция параметра
—
детерминистическая функция параметра ![]() .
Такая функция
называется траекто́рией или реализа́цией случайной
функции
.
.
Такая функция
называется траекто́рией или реализа́цией случайной
функции
.
[править]Примеры
 ,
где
,
где  называется
стандартной гауссовской
(нормальной) случайной
последовательностью.
называется
стандартной гауссовской
(нормальной) случайной
последовательностью.Пусть
 ,
и
,
и  —
случайная величина. Тогда
—
случайная величина. Тогда
![]()
является случайным процессом.
15.Корелционный анализ. Взаимная кореляция. Автокореляция. Корреляционный анализ (correlation analysis) [лат. correlatio — соотношение ] - раздел математической статистики, объединяющий практические методы исследования корреляционной связи между двумя и более случайными признаками или факторами.
Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной X, произойдет одновременно с пропорциональным изменением значения Y.
Корреляционная связь не предполагает причинной зависимости между переменными. Корреляционный анализ может использоваться для определения тесноты и направления связи и в причинных моделях. Инструментами корреляционного анализа являются разнообразные меры связи. Выбор мер (коэффициентов) связи зависит от способов измерения переменных и характера связи между ними.
Для количественных, порядковых и дихотомических переменных используются понятия прямой и обратной связи. Связь между количественными и/или порядковыми переменными является прямой, если значения двух переменных одновременно возрастают или убывают; обратной - если возрастание значений одной переменной сопровождается убыванием значений второй.
Для дихотомических переменных связь является прямой, если измеряемые ими свойства объектов чаще встречаются или не встречаются одновременно, чем порознь; обратной - если соответствующие свойства чаще встречаются порознь.
Для номинальных переменных, за исключением дихотомических, понятия прямой и обратной связи не определены, связь между ними рассматривается как ненаправленная.
Отдельную методологическую проблему представляет так называемая «ложная корреляционная зависимость», проявляющаяся в корреляционной связи (иногда достаточно сильной) между переменными, которые заведомо не могут взаимно обусловливать друг друга. Причиной обычно является наличие некого неучтенного в анализе фактора, который влияет на каждую из исследуемых переменных. Например,корреляция сорта губной помады с политическими убеждениями женщины объясняется ее общественным положением и уровнем благосостояния. Ложные корреляции, так же, как вызывающие их факторы, могут быть выявлены только в результате глубокого теоретического анализа структуры связей между переменными. Для их устранения применяется аппарат коэффициентов частной корреляции.
Взаимная
Взаимнокорреляционная функция — стандартный метод оценки степени корреляции двух последовательностей. Она часто используется для поиска в длинной последовательности более короткой заранее известной. Рассмотрим два ряда f и g. Взаимная корреляция определяется по формуле:
![]() ,
,
где i — сдвиг между последовательностями относительно друг друга, а верхний индекс в виде звёздочки означает комплексное сопряжение. В общем случае, для непрерывных функций f (t) и g (t) взаимная корреляция определяется как
![]()
Если ![]() и
—
два независимых случайных
числа с функциями
распределения вероятностей соответственно f и g,
тогда взаимная корреляция f
и
—
два независимых случайных
числа с функциями
распределения вероятностей соответственно f и g,
тогда взаимная корреляция f ![]() g соответствует
распределению вероятностей выражения
g соответствует
распределению вероятностей выражения ![]() .
Напротив, свёртка f
.
Напротив, свёртка f ![]() g соответствует
распределению вероятностей суммы
g соответствует
распределению вероятностей суммы ![]() .
.
[править]Свойства
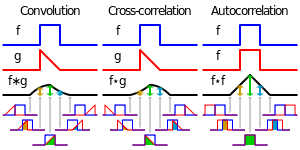
Слева направо: свёртка, взаимная корреляция и автокорреляция
Взаимная корреляция и свёртка взаимосвязанны:
![]()
поэтому, если функции f и g чётны, то
![]()
Также: ![]()
По аналогии с теоремой свёртки взаимная корреляция удовлетворяет
![]()
где ![]() означает преобразование
Фурье.
Данное свойство часто используется
вместе с алгоритмами быстрого
преобразования Фурье для
эффективного вычисления величины
взаимной корреляции.
означает преобразование
Фурье.
Данное свойство часто используется
вместе с алгоритмами быстрого
преобразования Фурье для
эффективного вычисления величины
взаимной корреляции.
Автокорреляция Автокорреляция — статистическая взаимосвязь между последовательностями величин одного ряда, взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Данное понятие широко используется в эконометрике. Наличие автокорреляции случайных ошибок регрессионной модели приводит к ухудшению качества МНК-оценок параметров регрессии, а также к завышению тестовых статистик, по которым проверяется качество модели (то есть создается искусственное улучшение качества модели относительно её действительного уровня точности). Поэтому тестирование автокорреляции случайных ошибок является необходимой процедурой построения регрессионной модели.
Коэффициенты автокорреляции также имеют самостоятельное важное значение для моделей временных рядов ARMA.
[править]Тестирование автокорреляции
Чаще всего тестируется наличие в случайных ошибках авторегрессионного процесса первого порядка. Для тестирования нулевой гипотезы, о равенстве коэффициента автокорреляции нулю чаще всего применяют критерий Дарбина-Уотсона. При наличии лаговой зависимой переменной в модели данный критерий неприменим, можно использовать асимптотический h-тест Дарбина. Оба эти теста предназначены для проверки автокорреляции случайных ошибок первого порядка. Для тестирования автокорреляции случайных ошибок большего порядка можно использовать более универсальный асимптотический LM-тест Бройша-Годфри. В данном тесте случайные ошибки не обязательно должны быть нормально распределены. Тест применим также и в авторегрессионных моделях (в отличие от критерия Дарбина-Уотсона).
Для тестирования совместной гипотезы о равенстве нулю всех коэффициентов автокорреляции до некоторого порядка можно использовать Q-тест Бокса — Пирса или Q-тест Льюнга-Бокса
[править]Автокорреляционная функция
Автокорреляционная функция показывает зависимость автокорреляции от величины сдвига во времени. При этом предполагается стационарность временного ряда, означающая в том числе независимость автокорреляций от момента времени. Анализ автокорреляционной функции (вместе с частной автокорреляционной функцией) позволяет проводить идентификацию порядка ARMA-моделей.
