4.Энергетические характеристики сигналов

Основными энергетическими характеристиками сигнала s(t) являются его мощность иэнергия.

Мгновенная мощность p(t) для вещественного сигнала определяется как

а для комплексного как

где знак " * " означает комплексно сопряженную функцию.

Если s(t) - напряжение или ток, то p(t) есть мгновенная мощность, выделяемая на сопротивлении   1 Ом.

Энергия сигнала на интервале ( t₂ , t₁ ) определяется как интеграл от мгновенной мощности

Отношение

имеет смысл средней на интервале ( t₂ , t₁ ) мощности.

Для неограниченных по времени периодических сигналов определяют среднюю за период мощность

5.Расположение в ряд Фурье

Ряд Фурье — представление произвольной функции   с периодом   в виде ряда

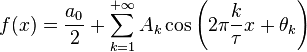
Этот ряд может быть также переписан в виде

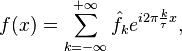
где

 — амплитуда  -го гармонического колебания,

 — круговая частота гармонического колебания,

 — начальная фаза  -го колебания,

 —  -я комплексная амплитуда

В более общем виде рядом Фурье элемента гильбертова пространства называется разложение этого элемента по ортогональному базису. Существует множество систем ортогональных функций: Уолша, Лагера, Котельникова и др.

Разложение функции в ряд Фурье является мощным инструментом при решении самых разных задач благодаря тому, что ряд Фурье прозрачным образом ведёт себя при дифференцировании, интегрировании, сдвиге функции по аргументу и свёртке функций.

6.Преобразование Фурье

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Преобразование Фурье функции   вещественной переменной является интегральным и задаётся следующей формулой:

Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.

Хотя формула, задающая преобразование Фурье, имеет ясный смысл только для функций класса  , преобразование Фурье может быть определено и для более широкого класса функций и даже обобщённых функций. Это возможно благодаря ряду свойств преобразования Фурье:

• Преобразование Фурье является линейным оператором:

• Справедливо равенство Парсеваля: если  , то преобразование Фурье сохраняет  -норму:

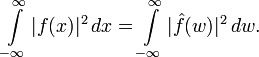
Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство  . Равенство Парсеваля будет при этом справедливо для всех  .

• Формула обращения:

справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция   является достаточно гладкой. Если  , то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.

Эта формула объясняет физический смысл преобразования Фурье: правая часть — (бесконечная) сумма гармонических колебаний   с частотами  , амплитудами   и фазовыми сдвигами  соответственно.

• Теорема о свёртке: если  , тогда

, где

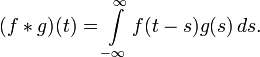
Эта формула может быть распространена и на случай обобщённых функций.

• Преобразование Фурье и дифференцирование. Если  , то

Из этой формулы легко выводится формула для  -й производной:

Формулы верны и в случае обобщённых функций.

• Преобразование Фурье и сдвиг.

Эта и предыдущая формула являются частными случаями теоремы о свёртке, так как сдвиг по аргументу — это свёртка со сдвинутой дельта-функцией  , а дифференцирование — свёртка с производной дельта-функции.

• Преобразование Фурье и растяжение.

• Преобразование Фурье обобщённых функций. Преобразование Фурье можно определить для широкого класса обобщённых функций. Определим вначале пространство гладких быстро убывающих функций (пространство Шварца):

Ключевым свойством этого пространства является то, что это инвариантное подпространство по отношению к преобразованию Фурье.

Теперь определим его двойственное пространство  . Это некоторое подпространство в пространстве всех обобщённых функций — так называемые обобщённые функции медленного роста. Теперь для функции   её преобразованием Фурье называется обобщённая функция  , действующая на основные функции по правилу

Например, вычислим преобразование Фурье дельта-функции:

Таким образом, преобразованием Фурье дельта-функции является константа  .