- •Подпись преподавателя _________________________
- •Подпись преподавателя _________________________
- •Подпись преподавателя _________________________
- •Подпись преподавателя _________________________
- •Подпись преподавателя _________________________
- •Подпись преподавателя _________________________
- •Подпись преподавателя _________________________
- •Подпись преподавателя _________________________
- •Подпись преподавателя _________________________
- •Подпись преподавателя _________________________
Тестовое задание для проведения экзамена по дисциплине «Эконометрика» для студентов очной формы обучения Вариант № 1 Фамилия И.О._______________________________________ Группа_____________________________________________ Уважаемые студенты, отметьте в каждом задании один (и только один) правильный на Ваш взгляд ответ, например, обведя его или перечеркнув.
Задание № 1.
Уравнение
регрессии имеет вид:
Задание № 2. Экономический показатель Х представлен выборкой:
Тогда выборочное среднее величины Х равно:
Задание № 3. В
результате анализа корреляционной
зависимости между показателями X
и Y,
оказалось, что связь между факторами
значимая и однонаправленная (с ростом
показателя X,
показатель Y
в среднем растет). Тогда коэффициент
парной корреляции
Задание № 4.
Коэффициент
парной корреляции факторов X
и Y
равен
Задание № 5.
Для
определения связи между ценой на товар
X
и спросом Y
была взята выборка этих показателей
объемом
|
Задание № 6.
Исследуется
зависимость между двумя экономическими
показателями X
и Y.
На основании опытных данных были
построены 4 уравнения регрессии и
рассчитаны коэффициенты корреляции
для следующих моделей: линейная
(
=0,74);
гиперболическая
Задание № 7.
При
построении множественной линейной
модели
Задание № 8.
Индекс
множественной корреляции
линейной
модели
равен R=0,76.
Число наблюдений
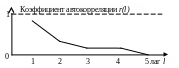
Задание № 9. Временной ряд имеет коррелограмму вида:
Это подтверждает, что временной ряд: Варианты ответов:
Задание № 10. Временной ряд имеет вид: 3,5,5,7,9,11,17. Тогда простая двухчленная скользящая средняя имеет вид:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Оценка_____________________________
Подпись преподавателя _________________________
Тестовое задание для проведения экзамена по дисциплине «Эконометрика» для студентов очной формы обучения Вариант № 2 Фамилия И.О._______________________________________ Группа_____________________________________________ Уважаемые студенты, отметьте в каждом задании один (и только один) правильный на Ваш взгляд ответ, например, обведя его или перечеркнув.
Задание № 1.
Уравнение
регрессии имеет вид:
Задание № 2. Экономический показатель Х представлен выборкой:
Тогда выборочное среднее величины Х равно:
Задание № 3. В результате анализа корреляционной зависимости между показателями X и Y, оказалось, что связь между факторами значимая и однонаправленная (с ростом показателя X, показатель Y в среднем растет). Тогда коэффициент парной корреляции может быть равен:
Задание № 4.
Коэффициент парной корреляции
факторов X и Y равен
Задание № 5. Для определения связи между ценой на товар X и спросом Y была взята выборка этих показателей объемом . По этим данным была построена линейная регрессионная модель и рассчитан парный коэффициент корреляции =-0,61. Для проверки его значимости была вычислена статистика (наблюдаемое значение) t-критерия Стьюдента. Она оказалась равна:
|
Задание № 6. Исследуется зависимость между двумя экономическими показателями X и Y. На основании опытных данных были построены 4 уравнения регрессии и рассчитаны коэффициенты корреляции для следующих моделей: линейная ( =0,76); гиперболическая ( =0,64); степенная ( =0,85) и показательная ( =0,53). На основании опытных данных, исследуемая зависимость описывается лучше всего моделью:
Задание № 7. При построении множественной линейной модели были получены парные коэффициенты корреляции =-0,45, =0,93, =-0,93. Какой из факторов X или Y сильнее влияет на результирующую функцию Z.
Задание № 8. Индекс множественной корреляции линейной модели равен R=0,79. Число наблюдений . Для оценки значимости индекса множественной корреляции была рассчитана F-статистика критерия Фишера. Она равна:
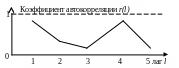
Задание № 9. Временной ряд имеет коррелограмму вида:
Это подтверждает, что временной ряд: Варианты ответов:
Задание № 10. Временной ряд имеет вид: 7,5,5,3,3,1,1. Тогда простая двухчленная скользящая средняя имеет вид:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Оценка_____________________________