Климов ПМИ, МКН - 2 семестр экзамен

1. Определение и свойства верхнего и нижнего интегралов (21-25)

2. Определение интеграла Римана. Критерий Римана интегрируемости (25-26)

3. Интегрируемость непрерывных и монотонных функций (26-27)

4. Операции над интегрируемыми функциями. Свойства интеграла (28-29)

5. Интеграл с переменным верхним пределом (29-30)

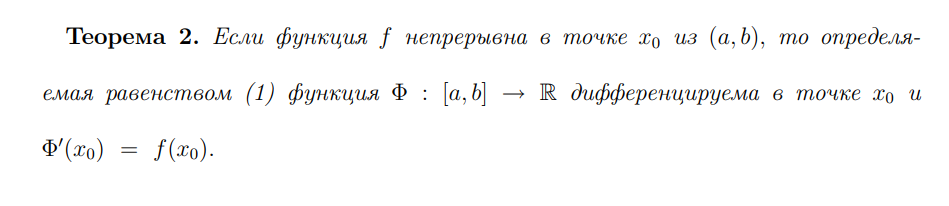
6. Формула Ньютона-Лейбница (33-34)

7. Замена переменной в интеграле Римана (34-35)

8. Квадрируемые фигуры (35-37)

9. Площадь криволинейной трапеции (37-39)

10. Определение и простейшие свойства несобственных интегралов

11. Признаки сравнения несобственных интегралов

10. Площадь криволинейного сектора (37-38)

12. Комплексные числа и комплексные последовательности (74-75)

13. Ряды с комплексными элементами (75-76)

14. Признаки сравнения

15. Признаки Коши, Даламбера и Раабе (76-78)

16. Интегральный признак сходимости ряда (78-80)

17. Критерий Коши равномерной сходимости (89-91)

18. Равномерная сходимость и непрерывность (91-92)

19. Интегрирование функциональных последовательностей и рядов (92-93)

20. Сходимости функциональных рядов. Признак Вейерштрасса (93-94)

21. Радиус сходимости степенного ряда (95-96)

22. Равномерная сходимость степенного ряда (100-101)

23. Дифференцируемость и интегрируемость степенного ряда (105-107)

24. Степенные ряды для элементарных функций (e^x, cos x, sin x, ln(1+x), (1+x)^m) (104-105)

25. Экспонента, косинус и синус комплексного аргумента (102-103)

26. Пространства со скалярным произведением

27. Ортонормированные системы

28. Коэффициенты Фурье

29. Полные ортонормированные системы

30. Формулы Эйлера-Фурье

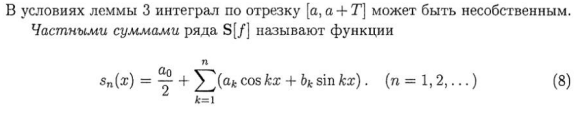
32. Сходимость Тригонометрического ряда в точке. Признак локализации