Решение задачи коммивояжера алгоритмом Литтла
 Пусть
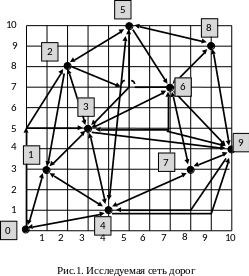
задана сеть дорог, показанная на рис.1
и соединяющая 10 городов.
Пусть
задана сеть дорог, показанная на рис.1
и соединяющая 10 городов.
Требуется найти минимальный гамильтонов путь для этой сети, т.е. найти маршрут минимальной длины, начинающийся, например, с города 0 и заканчивающийся в нем же и проходящий через каждый город ровно один раз (т.е. решить задачу коммивояжера). Решение надо найти тремя способами: 1) используя алгоритм Литтла, 2) используя электронные таблицы Excell и 3) используя специально разработанную для этого программу на основе нейронной сети Хопфилда.
Заполняем матрицу расстояний, соответствующую рис.1. (Таблица 1).
-
Таблица 1
0
1
2
3
4
5
6
7
8
9
0
-----
3,16
8,61
8,00
4,12
∞
∞
∞
∞
∞
1
3,16
-----
∞
2,83
3,61
∞
∞
∞
∞
∞
2
∞
5,10
-----
3,16
∞
3,61
∞
∞
∞
∞
3
∞
2,83
3,16
-----
4,12
∞
4,47
∞
∞
7,07
4
4,12
3,61
∞
4,12
-----
∞
∞
4,47
∞
8,16
5
∞
∞
3,61
5,83
∞
-----
∞
∞
4,12
∞
6
∞
∞
5,16
∞
∞
3,61
-----
4,12
2,83
4,24
7
∞
∞
∞
∞
4,47
∞
4,12
-----
∞
2,24
8
∞
∞
∞
∞
∞
4,12
2,83
∞
-----
5,10
9
∞
∞
∞
7,16
7,61
∞
5,16
2,24
5,10
-----
Используя алгоритм Флойда, рассчитываем матрицу кратчайших расстояний между всеми городами. Последовательность действий в соответствии с алгоритмом Флойда была рассмотрена в лекционных материалах курса и здесь приводятся только получаемые на каждом шаге матрица расстояний Di и матрица последовательности узлов Si.
D0 |
|
||||||||||
k=0 |
----- |
3,16 |
8,61 |
8,00 |
4,12 |
∞ |
∞ |
∞ |
∞ |
∞ |
|
|
3,16 |
----- |
∞ |
2,83 |
3,61 |
∞ |
∞ |
∞ |
∞ |
∞ |
|
∞ |
5,10 |
----- |
3,16 |
∞ |
3,61 |
∞ |
∞ |
∞ |
∞ |
||
∞ |
2,83 |
3,16 |
----- |
4,12 |
∞ |
4,47 |
∞ |
∞ |
7,07 |
||
4,12 |
3,61 |
∞ |
4,12 |
----- |
9,06 |
∞ |
4,47 |
∞ |
8,16 |
||
∞ |
∞ |
3,61 |
5,83 |
9,06 |
----- |
∞ |
∞ |
4,12 |
∞ |
||
∞ |
∞ |
5,16 |
∞ |
∞ |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
∞ |
∞ |
∞ |
∞ |
4,47 |
∞ |
4,12 |
----- |
∞ |
2,24 |
||
∞ |
∞ |
∞ |
∞ |
∞ |
4,12 |
2,83 |
∞ |
----- |
5,10 |
||
∞ |
∞ |
∞ |
7,16 |
7,61 |
∞ |
5,16 |
2,24 |
5,10 |
----- |
||
S0 |
|||||||||
--- |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
- |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
--- |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
--- |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
--- |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
--- |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
--- |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
--- |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
--- |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
--- |
S1 |
|||||||||
--- |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
--- |
0 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
--- |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
--- |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
0 |
3 |
--- |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
--- |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
--- |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
--- |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
--- |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
--- |
D1 |
|
||||||||||
k=1 |
----- |
3,16 |
8,61 |
8 ,00 |
4,12 |
∞ |
∞ |
∞ |
∞ |
∞ |
|
3,16 |
----- |
11,77 |
2,83 |
3,61 |
∞ |
∞ |
∞ |
∞ |
∞ |
||
∞ |
5,10 |
----- |
3,16 |
∞ |
3,61 |
∞ |
∞ |
∞ |
∞ |
||
∞ |
2,83 |
3,16 |
----- |
4,12 |
∞ |
4,47 |
∞ |
∞ |
7,07 |
||
4,12 |
3,61 |
12,73 |
4,12 |
----- |
9,06 |
∞ |
4,47 |
∞ |
8,16 |
||
∞ |
∞ |
3,61 |
5,83 |
9,06 |
----- |
∞ |
∞ |
4,12 |
∞ |
||
∞ |
∞ |
5,16 |
∞ |
∞ |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
∞ |
∞ |
∞ |
∞ |
4,47 |
∞ |
4,12 |
----- |
∞ |
2,24 |
||
∞ |
∞ |
∞ |
∞ |
∞ |
4,12 |
2,83 |
∞ |
----- |
5,10 |
||
∞ |
∞ |
∞ |
7,16 |
7,61 |
∞ |
5,16 |
2,24 |
5,10 |
----- |
||
S2 |
|||||||||
--- |
1 |
2 |
1 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
--- |
0 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
1 |
--- |
3 |
1 |
5 |
6 |
7 |
8 |
9 |
1 |
1 |
2 |
--- |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
0 |
3 |
--- |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
--- |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
--- |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
--- |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
--- |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
--- |
D2 |
|
||||||||||
k=2 |
----- |
3,16 |
8,61 |
5,99 |
4,12 |
∞ |
∞ |
∞ |
∞ |
∞ |
|
3,16 |
----- |
11,77 |
2,83 |
3,61 |
∞ |
∞ |
∞ |
∞ |
∞ |
||
8,26 |
5,10 |
----- |
3,16 |
8,71 |
3,61 |
∞ |
∞ |
∞ |
∞ |
||
5,99 |
2,83 |
3,16 |
----- |
4,12 |
∞ |
4,47 |
∞ |
∞ |
7,07 |
||
4,12 |
3,61 |
12,73 |
4,12 |
----- |
9,06 |
∞ |
4,47 |
∞ |
8,16 |
||
∞ |
∞ |
3,61 |
5,83 |
9,06 |
----- |
∞ |
∞ |
4,12 |
∞ |
||
∞ |
∞ |
5,16 |
∞ |
∞ |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
∞ |
∞ |
∞ |
∞ |
4,47 |
∞ |
4,12 |
----- |
∞ |
2,24 |
||
∞ |
∞ |
∞ |
∞ |
∞ |
4,12 |
2,83 |
∞ |
----- |
5,10 |
||
∞ |
∞ |
∞ |
7,16 |
7,61 |
∞ |
5,16 |
2,24 |
5,10 |
----- |
||
S3 |
|||||||||
--- |
1 |
2 |
1 |
4 |
2 |
6 |
7 |
8 |
9 |
0 |
- -- |
0 |
3 |
4 |
2 |
6 |
7 |
8 |
9 |
1 |
1 |
--- |
3 |
1 |
5 |
6 |
7 |
8 |
9 |
1 |
1 |
2 |
--- |
4 |
2 |
6 |
7 |
8 |
9 |
0 |
1 |
0 |
3 |
--- |
5 |
6 |
7 |
8 |
9 |
2 |
2 |
2 |
3 |
4 |
- -- |
6 |
7 |
8 |
9 |
2 |
2 |
2 |
2 |
2 |
5 |
--- |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
--- |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
--- |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
--- |
D3 |
|
||||||||||
k |
----- |
3,16 |
8,61 |
5,99 |
4,12 |
12,22 |
∞ |
∞ |
∞ |
∞ |
|
3,16 |
----- |
1 |
2,83 |
3,61 |
1 5,37 |
∞ |
∞ |
∞ |
∞ |
||
8,26 |
5,10 |
----- |
3,16 |
8 ,71 |
3,61 |
∞ |
∞ |
∞ |
∞ |
||
5,99 |
2,83 |
3,16 |
----- |
4,12 |
6,77 |
4,47 |
∞ |
∞ |
7,07 |
||
4,12 |
3 ,61 |
12,73 |
4,12 |
----- |
9,06 |
∞ |
4,47 |
∞ |
8 ,16 |
||
11,87 |
8 ,71 |
3,61 |
5,83 |
9,06 |
----- |
∞ |
∞ |
4,12 |
∞ |
||
13,42 |
10,26 |
5,16 |
8,32 |
13,87 |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
∞ |
∞ |
∞ |
∞ |
4,47 |
∞ |
4,12 |
----- |
∞ |
2,24 |
||
∞ |
∞ |
∞ |
∞ |
∞ |
4,12 |
2,83 |
∞ |
----- |
5,10 |
||
∞ |
∞ |
∞ |
7,16 |
7,61 |
∞ |
5,16 |
2,24 |
5,10 |
----- |
||
S4 |
|||||||||
--- |
1 |
2 |
1 |
4 |
2 |
3 |
7 |
8 |
3 |
0 |
--- |
3 |
3 |
4 |
3 |
3 |
7 |
8 |
3 |
1 |
1 |
--- |
3 |
3 |
5 |
3 |
7 |
8 |
3 |
1 |
1 |
2 |
--- |
4 |
2 |
6 |
7 |
8 |
9 |
0 |
1 |
3 |
3 |
--- |
5 |
3 |
7 |
8 |
9 |
3 |
3 |
2 |
3 |
4 |
--- |
3 |
7 |
8 |
3 |
2 |
2 |
2 |
2 |
3 |
5 |
--- |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
--- |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
--- |
9 |
3 |
3 |
3 |
3 |
4 |
3 |
6 |
7 |
8 |
--- |
D4 |
|
||||||||||
k=4 |
----- |
3,16 |
8,61 |
5,99 |
4,12 |
12,22 |
10,46 |
∞ |
∞ |
1 3,06 |
|
3,16 |
----- |
5,99 |
2,83 |
3,61 |
9,60 |
7,30 |
∞ |
∞ |
9,90 |
||
8,26 |
5,10 |
----- |
3,16 |
7,28 |
3,61 |
7,63 |
∞ |
∞ |
10,23 |
||
5,99 |
2,83 |
3,16 |
----- |
4,12 |
6,77 |
4,47 |
∞ |
∞ |
7,07 |
||
4,12 |
3,61 |
7,28 |
4,12 |
----- |
9,06 |
8,59 |
4,47 |
∞ |
8,16 |
||
11,82 |
8,66 |
3,61 |
5,83 |
9,06 |
----- |
10.30 |
∞ |
4,12 |
12,90 |
||
13,42 |
10,26 |
5,16 |
8,32 |
12,44 |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
∞ |
∞ |
∞ |
∞ |
4,47 |
∞ |
4,12 |
----- |
∞ |
2,24 |
||
∞ |
∞ |
∞ |
∞ |
∞ |
4,12 |
2,83 |
∞ |
----- |
5,10 |
||
1 3,15 |
9,99 |
10,32 |
7,16 |
7,61 |
13,93 |
5,16 |
2,24 |
5,10 |
----- |
||
S5 |
|||||||||
--- |
1 |
2 |
1 |
4 |
2 |
3 |
4 |
8 |
4 |
0 |
--- |
3 |
3 |
4 |
3 |
3 |
4 |
8 |
3 |
1 |
1 |
--- |
3 |
3 |
5 |
3 |
4 |
8 |
3 |
1 |
1 |
2 |
--- |
4 |
2 |
6 |
4 |
8 |
9 |
0 |
1 |
3 |
3 |
--- |
5 |
3 |
7 |
8 |
9 |
3 |
3 |
2 |
3 |
4 |
--- |
3 |
4 |
8 |
3 |
2 |
2 |
2 |
2 |
3 |
5 |
--- |
7 |
8 |
9 |
4 |
4 |
4 |
4 |
4 |
4 |
6 |
- -- |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
--- |
9 |
4 |
3 |
3 |
3 |
4 |
3 |
6 |
7 |
8 |
--- |
D5 |
|
||||||||||
k=5 |
----- |
3,16 |
8,61 |
5,99 |
4,12 |
12,22 |
10,46 |
8,59 |
∞ |
12,28 |
|
3,16 |
----- |
5,99 |
2,83 |
3,61 |
9,60 |
7,30 |
8 ,08 |
∞ |
9,90 |
||
8,26 |
5,10 |
----- |
3,16 |
7,28 |
3,61 |
7,63 |
11,75 |
∞ |
10,23 |
||
5,99 |
2,83 |
3,16 |
----- |
4,12 |
6,77 |
4,47 |
8,59 |
∞ |
7,07 |
||
4,12 |
3,61 |
7,28 |
4,12 |
----- |
9,06 |
8,59 |
4 ,47 |
∞ |
8,16 |
||
11,82 |
8,66 |
3,61 |
5,83 |
9,06 |
----- |
10,30 |
13,53 |
4,12 |
12,90 |
||
13,42 |
10,26 |
5,16 |
8,32 |
12,44 |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
8,59 |
8,08 |
11,75 |
8,59 |
4,47 |
13,53 |
4,12 |
- ---- |
∞ |
2,24 |
||
∞ |
∞ |
∞ |
∞ |
∞ |
4,12 |
2,83 |
∞ |
----- |
5,10 |
||
11,73 |
9,99 |
10,32 |
7,16 |
7,61 |
13,93 |
5,16 |
2,24 |
5,10 |
----- |
||
S6 |
|||||||||
--- |
1 |
2 |
1 |
4 |
2 |
3 |
4 |
5 |
4 |
0 |
--- |
3 |
3 |
4 |
3 |
3 |
4 |
5 |
3 |
1 |
1 |
--- |
3 |
3 |
5 |
3 |
4 |
5 |
3 |
1 |
1 |
2 |
--- |
4 |
2 |
6 |
4 |
5 |
9 |
0 |
1 |
3 |
3 |
--- |
5 |
3 |
7 |
5 |
9 |
3 |
3 |
2 |
3 |
4 |
--- |
3 |
4 |
8 |
3 |
2 |
2 |
2 |
2 |
3 |
5 |
--- |
7 |
8 |
9 |
4 |
4 |
4 |
4 |
4 |
4 |
6 |
- -- |
5 |
9 |
5 |
5 |
5 |
5 |
5 |
5 |
6 |
5 |
--- |
9 |
4 |
3 |
3 |
3 |
4 |
3 |
6 |
7 |
8 |
--- |
D6 |
|
||||||||||
k=6 |
----- |
3,16 |
8,61 |
5,99 |
4,12 |
12,22 |
10,46 |
8,59 |
1 6,34 |
12,28 |
|
3,16 |
----- |
5,99 |
2,83 |
3,61 |
9,60 |
7,30 |
8,08 |
1 3,72 |
9,90 |
||
8,26 |
5,10 |
----- |
3,16 |
7,28 |
3,61 |
7,63 |
11,75 |
7,73 |
10,23 |
||
5,99 |
2,83 |
3,16 |
----- |
4,12 |
6,77 |
4,47 |
8,59 |
1 0,89 |
7,07 |
||
4,12 |
3,61 |
7,28 |
4,12 |
----- |
9,06 |
8,59 |
4,47 |
1 3,18 |
8,16 |
||
11,82 |
8,66 |
3,61 |
5,83 |
9,06 |
----- |
10,30 |
13,53 |
4,12 |
12,90 |
||
13,42 |
10,26 |
5,16 |
8,32 |
12,44 |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
8,59 |
8,08 |
1 1,75 |
8,59 |
4,47 |
1 3,53 |
4,12 |
----- |
1 7,65 |
2,24 |
||
15,94 |
12,78 |
7,73 |
9,95 |
13,18 |
4,12 |
2,83 |
1 7,65 |
----- |
5,10 |
||
11,73 |
9,99 |
10,32 |
7,16 |
7,61 |
1 3,93 |
5,16 |
2,24 |
5,10 |
----- |
||
S7 |
|||||||||
--- |
1 |
2 |
1 |
4 |
2 |
3 |
4 |
6 |
4 |
0 |
--- |
3 |
3 |
4 |
3 |
3 |
4 |
6 |
3 |
1 |
1 |
--- |
3 |
3 |
5 |
3 |
4 |
5 |
3 |
1 |
1 |
2 |
--- |
4 |
2 |
6 |
4 |
6 |
9 |
0 |
1 |
3 |
3 |
--- |
5 |
3 |
7 |
6 |
9 |
3 |
3 |
2 |
3 |
4 |
--- |
3 |
4 |
8 |
3 |
2 |
2 |
2 |
2 |
3 |
5 |
--- |
7 |
8 |
9 |
4 |
4 |
6 |
4 |
4 |
6 |
6 |
--- |
6 |
9 |
5 |
5 |
5 |
5 |
5 |
5 |
6 |
6 |
--- |
9 |
4 |
3 |
3 |
3 |
4 |
6 |
6 |
7 |
8 |
--- |
D7 |
|
||||||||||
k=7 |
----- |
3,16 |
8,61 |
5,99 |
4,12 |
12,22 |
10,46 |
8,59 |
13,29 |
1 2,28 |
|
3,16 |
----- |
5,99 |
2,83 |
3,61 |
9,60 |
7,30 |
8,08 |
10,13 |
9,90 |
||
8,26 |
5,10 |
----- |
3,16 |
7,28 |
3,61 |
7,63 |
11,75 |
7,73 |
10,23 |
||
5,99 |
2,83 |
3,16 |
----- |
4,12 |
6,77 |
4,47 |
8,59 |
7,30 |
7,07 |
||
4,12 |
3,61 |
7,28 |
4,12 |
----- |
9,06 |
8,59 |
4,47 |
11,42 |
8 ,16 |
||
11,82 |
8,66 |
3,61 |
5,83 |
9,06 |
----- |
10,30 |
13,53 |
4,12 |
12,90 |
||
1 3,42 |
10,26 |
5,16 |
8,32 |
1 2,44 |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
8,59 |
8,08 |
9,28 |
8,59 |
4,47 |
7,73 |
4,12 |
----- |
6,95 |
2,24 |
||
1 5,94 |
12,78 |
7,73 |
9,95 |
1 3,18 |
4,12 |
2,83 |
6,95 |
----- |
5,10 |
||
1 1,73 |
9,99 |
10,32 |
7,16 |
7 ,61 |
8,77 |
5,16 |
2,24 |
5,10 |
----- |
||
S8 |
|||||||||
--- |
1 |
2 |
1 |
4 |
2 |
3 |
4 |
6 |
7 |
0 |
--- |
3 |
3 |
4 |
3 |
3 |
4 |
6 |
3 |
1 |
1 |
--- |
3 |
3 |
5 |
3 |
4 |
5 |
3 |
1 |
1 |
2 |
--- |
4 |
2 |
6 |
4 |
6 |
9 |
0 |
1 |
3 |
3 |
--- |
5 |
3 |
7 |
6 |
7 |
3 |
3 |
2 |
3 |
4 |
- -- |
3 |
4 |
8 |
3 |
7 |
2 |
2 |
2 |
7 |
5 |
--- |
7 |
8 |
9 |
4 |
4 |
6 |
4 |
4 |
6 |
6 |
--- |
6 |
9 |
7 |
5 |
5 |
5 |
7 |
5 |
6 |
6 |
--- |
9 |
7 |
3 |
3 |
3 |
7 |
6 |
6 |
7 |
8 |
--- |
D8 |
|
||||||||||
k=8 |
----- |
3,16 |
8,61 |
5,99 |
4,12 |
12,22 |
10,46 |
8,59 |
13,29 |
10,83 |
|
3,16 |
----- |
5,99 |
2,83 |
3,61 |
9,60 |
7,30 |
8,08 |
10,13 |
9,90 |
||
8,26 |
5,10 |
----- |
3,16 |
7,28 |
3,61 |
7,63 |
11,75 |
7,73 |
10,23 |
||
5,99 |
2,83 |
3,16 |
----- |
4,12 |
6,77 |
4,47 |
8,59 |
7,30 |
7,07 |
||
4,12 |
3,61 |
7,28 |
4,12 |
----- |
9,06 |
8,59 |
4,47 |
11,42 |
6,71 |
||
11,82 |
8,66 |
3,61 |
5,83 |
9,06 |
----- |
1 0,30 |
1 3,53 |
4,12 |
1 2,90 |
||
12,71 |
10,26 |
5,16 |
8,32 |
8,59 |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
8,59 |
8,08 |
9,28 |
8,59 |
4,47 |
7,73 |
4,12 |
----- |
6,95 |
2,24 |
||
15,54 |
12,78 |
7,73 |
9,95 |
11,42 |
4,12 |
2,83 |
6,95 |
----- |
5,10 |
||
10,83 |
9,99 |
10,32 |
7,16 |
6,71 |
8,77 |
5,16 |
2,24 |
5,10 |
----- |
||
D9, Итог |
|
||||||||||
k=9 |
----- |
3,16 |
8,61 |
5,99 |
4,12 |
12,22 |
10,46 |
8,59 |
13,29 |
10,83 |
|
3,16 |
----- |
5,99 |
2,83 |
3,61 |
9,60 |
7,30 |
8,08 |
10,13 |
9,90 |
||
8,26 |
5,10 |
----- |
3,16 |
7,28 |
3,61 |
7,63 |
11,75 |
7,73 |
10,23 |
||
5,99 |
2,83 |
3,16 |
----- |
4,12 |
6,77 |
4,47 |
8,59 |
7,30 |
7,07 |
||
4,12 |
3,61 |
7,28 |
4,12 |
----- |
9,06 |
8,59 |
4,47 |
11,42 |
6,71 |
||
11,82 |
8,66 |
3,61 |
5,83 |
9,06 |
----- |
6,95 |
11,07 |
4,12 |
9,22 |
||
12,71 |
10,26 |
5,16 |
8,32 |
8,59 |
3,61 |
----- |
4,12 |
2,83 |
4,24 |
||
8,59 |
8,08 |
9,28 |
8,59 |
4,47 |
7,73 |
4,12 |
----- |
6,95 |
2,24 |
||
15,54 |
12,78 |
7,73 |
9,95 |
11,42 |
4,12 |
2,83 |
6,95 |
----- |
5,10 |
||
10,83 |
9,99 |
10,32 |
7,16 |
6,71 |
8,77 |
5,16 |
2,24 |
5,10 |
----- |
||
S9, Итог |
|||||||||
--- |
1 |
2 |
1 |
4 |
2 |
3 |
4 |
6 |
7 |
0 |
--- |
3 |
3 |
4 |
3 |
3 |
4 |
6 |
3 |
1 |
1 |
--- |
3 |
3 |
5 |
3 |
4 |
5 |
3 |
1 |
1 |
2 |
--- |
4 |
2 |
6 |
4 |
6 |
9 |
0 |
1 |
3 |
3 |
--- |
5 |
3 |
7 |
6 |
7 |
3 |
3 |
2 |
3 |
4 |
--- |
8 |
8 |
8 |
8 |
7 |
2 |
2 |
2 |
7 |
5 |
--- |
7 |
8 |
9 |
4 |
4 |
6 |
4 |
4 |
6 |
6 |
--- |
6 |
9 |
7 |
5 |
5 |
5 |
7 |
5 |
6 |
6 |
--- |
9 |
7 |
3 |
3 |
3 |
7 |
6 |
6 |
7 |
8 |
--- |
Используя полученные итоговые матрицы и табл.1, заполняем матрицу, служащую исходной для алгоритма Литтла, по следующему принципу: символ ∞ в табл.1 заменяем значением, полученным в табл.D9. Это значение соответствует минимальному пути между соответствующими пунктами. Сам маршрут между этими пунктами может быть получен из матрицы S9. В данном случае такими маршрутами будут:
перемещение 0-5: маршрут 0-2-5=5+3,61+3,61=12,22;
перемещение 0-6: маршрут 0-3-6=3,16+2,83+4,47=10,46;
перемещение 0-7: маршрут 0-4-7=4,12+4,47=8,59;
перемещение 0-8: маршрут 0-6-8=0-3-6-8=0-1-3-6-8=3,16+2,83+4,47+
+2,83=13,29;
перемещение 0-9: маршрут 0-7-9=0-4-7-9=4,12+4,47+2,24=10,83;
перемещение 1-2: маршрут 1-3-2=2,83+3,16=5,99;
перемещение 1-5: маршрут 1-3-2-5=2,83+3,16+3,61=9,60;
перемещение 1-6: маршрут 1-3-6=2,83+4,47=7,30;
перемещение 1-7: маршрут 1-4-7=3,61+4,47=8,08;
перемещение 1-8: маршрут 1-6-8=1-3-6-8=2,83+4,47+2,83=10,13;
перемещение 1-9: маршрут 1-3-9=2,83+7,07=9,90;
перемещение 2-0: маршрут 2-1-0=5,10+3,16=8,26;
перемещение 2-4: маршрут 2-3-4=3,16+4,12=7,28;
перемещение 2-6: маршрут 2-3-6=3,16+4,47=7,63;
перемещение 2-7: маршрут 2-4-7=2-3-4-7=3,16+4,12+4,47=11,75;
перемещение 2-8: маршрут 2-5-8=3,61+4,12=7,73;
перемещение 2-9: маршрут 2-3-9=3,16+7,07=10,23;
перемещение 3-0: маршрут 3-1-0=2,83+3,16=5,99;
перемещение 3-5: маршрут 3-2-5=3,16+3,61=6,77;
перемещение 3-7: маршрут 3-4-7=4,12+4,47=8,59;
перемещение 3-8: маршрут 3-6-8=4,47+2,83=7,30;
перемещение 4-2: маршрут 4-3-2=4,12+3,16=7,28;
перемещение 4-6: маршрут 4-3-6=4,12+4.47=8,59;
перемещение 4-8: маршрут 4-6-8=4-3-6-8=4,12+4.47+2,83=11,42;
перемещение 5-0: маршрут 5-3-1-0=3+2,83+2,83+3.16=11,82;
перемещение 5-1: маршрут 5-3-1=3+2,83+2,83=8,66;
перемещение 5-6: маршрут 5-8-6=4,12+2,83=6,95;
перемещение 5-7: маршрут 5-8-6-7=4,12+2,83+4,12=11,07;
перемещение 5-9: маршрут 5-8-9=4,12+5,10=9,22;
перемещение 6-0: маршрут 6-7-4-0=4,12+4,47+4,12=12,71;
перемещение 6-1: маршрут 6-2-1=2+3,16+5,10=10,26;
перемещение 6-3: маршрут 6-2-3=2+3,16+3,16=8,32;
перемещение 6-4: маршрут 6-7-4=4,12+4,47=8,59;
перемещение 7-0: маршрут 7-4-0=4,47+4,12=8,59;
перемещение 7-1: маршрут 7-4-1=4,47+3,61=8,08;
перемещение 7-2: маршрут 7-6-2=4,12+2+3,16=9,28;
перемещение 7-3: маршрут 7-4-3=4,47+4,12=8,59;
перемещение 7-5: маршрут 7-6-5=4,12+3,61=7,73;
перемещение 7-8: маршрут 7-6-8=4,12+2,83=6,95;
перемещение 8-0: маршрут 8-7-4-0=8-6-7-4-0=2,83+4,12+4,47+4,12
=15,54;
перемещение 8-1: маршрут 8-5-3-1=4,12+3+2,83+2,83=12,78;
перемещение 8-2: маршрут 8-5-2=4,12+3,61=7,73;
перемещение 8-3: маршрут 8-5-3=4,12+3+2,83=9,95;
перемещение 8-4: маршрут 8-7-4=8-6-7-4=2,83+4,12+4,47=11,42;
перемещение 8-7: маршрут 8-6-7=2,83+4,12=6,95;
перемещение 9-0: маршрут 9-7-4-0=2,24+4,47+4,12=10,83;
перемещение 9-1: маршрут 9-3-1=3,16+4+2,83=9,99;
перемещение 9-2: маршрут 9-3-2=7,16+3,16=10,32;
перемещение 9-5: маршрут 9-6-5=5,16+3,61=8,77;
В итоге начальная матрица для применения метода Литтла будет иметь вид табл.2.
-
Таблица 2
0
1
2
3
4
5
6
7
8
9
0
∞
3,16
8,61
8,00
4,12
12,22
10,46
8,59
13,29
10,83
1
3,16
∞
5,99
2,83
3,61
9,60
7,30
8,08
10,13
9,90
2
8,26
5,10
∞
3,16
7,28
3,61
7,63
11,75
7,73
10,23
3
5,99
2,83
3,16
∞
4,12
6,77
4,47
8,59
7,30
7,07
4
4,12
3,61
7,28
4,12
∞
9,06
8,59
4,47
11,42
8,16
5
11,82
8,66
3,61
5,83
9,06
∞
6,95
11,07
4,12
9,22
6
12,71
10,26
5,16
8,32
8,59
3,61
4,12
2,83
4,24
7
8,59
8,08
9,28
8,59
4,47
7,73
4,12
-----
6,95
2,24
8
15,54
12,78
7,73
9,95
11,42
4,12
2,83
6,95
-----
5,10
9
10,83
9,99
10,32
7,16
7,61
8,77
5,16
2,24
5,10
-----
Применяем алгоритм Литтла.
Находим минимальные элементы в каждой строке.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Минимумы строк |
0 |
∞ |
3,16 |
8,61 |
8,00 |
4,12 |
12,22 |
10,46 |
8,59 |
13,29 |
10,83 |
3,16 |
1 |
3,16 |
∞ |
5,99 |
2,83 |
3,61 |
9,60 |
7,30 |
8,08 |
10,13 |
9,90 |
2,83 |
2 |
8,26 |
5,10 |
∞ |
3,16 |
7,28 |
3,61 |
7,63 |
11,75 |
7,73 |
10,23 |
3,16 |
3 |
5,99 |
2,83 |
3,16 |
∞ |
4,12 |
6,77 |
4,47 |
8,59 |
7,30 |
7,07 |
2,83 |
4 |
4,12 |
3,61 |
7,28 |
4,12 |
∞ |
9,06 |
8,59 |
4,47 |
11,42 |
8,16 |
3,61 |
5 |
11,82 |
8,66 |
3,61 |
5,83 |
9,06 |
∞ |
6,95 |
11,07 |
4,12 |
9,22 |
3,61 |
6 |
12,71 |
10,26 |
5,16 |
8,32 |
8,59 |
3,61 |
∞ |
4,12 |
2,83 |
4,24 |
2,83 |
7 |
8,59 |
8,08 |
9,28 |
8,59 |
4,47 |
7,73 |
4,12 |
∞ |
6,95 |
2,24 |
2,24 |
8 |
15,54 |
12,78 |
7,73 |
9,95 |
11,42 |
4,12 |
2,83 |
6,95 |
∞ |
5,10 |
2,83 |
9 |
10,83 |
9,99 |
10,32 |
7,16 |
7,61 |
8,77 |
5,16 |
2,24 |
5,10 |
∞ |
2,24 |
Вычитаем минимальные элементы из остальных элементов строки.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,96 |
9,06 |
7,30 |
5,43 |
10,13 |
7,67 |
1 |
0,33 |
∞ |
3,16 |
0 |
0,78 |
6,77 |
4,47 |
5,25 |
7,30 |
7,07 |
2 |
5,10 |
1,94 |
∞ |
0 |
4,12 |
0,45 |
4,47 |
8,59 |
4,57 |
9,67 |
3 |
3,16 |
0 |
0,33 |
∞ |
1,29 |
3,94 |
1,64 |
5,76 |
4,47 |
4,24 |
4 |
0,51 |
0 |
3,67 |
0,51 |
∞ |
5,45 |
4,98 |
0,86 |
7,81 |
4,55 |
5 |
8,21 |
5,05 |
0 |
2,22 |
5,45 |
∞ |
3,34 |
7,46 |
0,51 |
5,61 |
6 |
9,88 |
7,43 |
2,33 |
5,49 |
5,76 |
0,78 |
∞ |
1,29 |
0 |
1,41 |
7 |
6,35 |
5,84 |
7,04 |
6,35 |
2,23 |
5,49 |
1,88 |
∞ |
4,71 |
0 |
8 |
12,71 |
9,95 |
4,90 |
7,12 |
8,59 |
1,29 |
0 |
4,12 |
∞ |
2,27 |
9 |
8,59 |
7,75 |
8,08 |
4,92 |
5,37 |
6,53 |
2,92 |
0 |
2,86 |
∞ |
Проделываем то же самое со столбцами, не содержащими нуля.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,96 |
9,06 |
7,30 |
5,43 |
10,13 |
7,67 |
1 |
0,33 |
∞ |
3,16 |
0 |
0,78 |
6,77 |
4,47 |
5,25 |
7,30 |
7,07 |
2 |
5,10 |
1,94 |
∞ |
0 |
4,12 |
0,45 |
4,47 |
8,59 |
4,57 |
9,67 |
3 |
3,16 |
0 |
0,33 |
∞ |
1,29 |
3,94 |
1,64 |
5,76 |
4,47 |
4,24 |
4 |
0,51 |
0 |
3,67 |
0,51 |
∞ |
5,45 |
4,98 |
0,86 |
7,81 |
4,55 |
5 |
8,21 |
5,05 |
0 |
2,22 |
5,45 |
∞ |
3,34 |
7,46 |
0,51 |
5,61 |
6 |
9,88 |
7,43 |
2,33 |
5,49 |
5,76 |
0,78 |
∞ |
1,29 |
0 |
1,41 |
7 |
6,35 |
5,84 |
7,04 |
6,35 |
2,23 |
5,49 |
1,88 |
∞ |
4,71 |
0 |
8 |
12,71 |
9,95 |
4,90 |
7,12 |
8,59 |
1,29 |
0 |
4,12 |
∞ |
2,27 |
9 |
8,59 |
7,75 |
8,08 |
4,92 |
5,37 |
6,53 |
2,92 |
0 |
2,86 |
∞ |
Минимумы столбцов |
0.33 |
|
|
|
0.78 |
0.45 |
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
7,30 |
5,43 |
10,13 |
7,67 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
4,47 |
5,25 |
7,30 |
7,07 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,47 |
8,59 |
4,57 |
9,67 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
1,64 |
5,76 |
4,47 |
4,24 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
4,98 |
0,86 |
7,81 |
4,55 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
3,34 |
7,46 |
0,51 |
5,61 |
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
∞ |
1,29 |
0 |
1,41 |
7 |
6,02 |
5,84 |
7,04 |
6,35 |
1,45 |
5,04 |
1,88 |
∞ |
4,71 |
0 |
8 |
12,38 |
9,95 |
4,90 |
7,12 |
7,81 |
0,84 |
0 |
4,12 |
∞ |
2,27 |
9 |
8,26 |
7,75 |
8,08 |
4,92 |
4,59 |
6,08 |
2,92 |
0 |
2,86 |
∞ |
Для каждого нулевого элемента рассчитываем значение Гij, равное сумме наименьшего элемента i строки (исключая элемент Cij=0) и наименьшего элемента j столбца.
Г01=0,18+0=0,18; Г10=0+0,18=0,18; Г13=0+0=0; Г14=0+0,18=0,18;
Г23=0+0=0; Г25=0+0,33=0,33; Г31=0,33+0=0,33; Г41=0,18+0=0,18;
Г52=0,51+0,33=0,84; Г68=0,33+0,51=0,84; Г79=1,45+1,41=2,86;
Г86=0,84+1,64=2,48; Г97=2,86+0,86=3,72.
Максимальный элемент Г97=3,72. Следовательно, ветвь 9-7 входит в маршрут.
Из матрицы удаляем строку 9 и столбец 7.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
7,30 |
10,13 |
7,67 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
4,47 |
7,30 |
7,07 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,47 |
4,57 |
9,67 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
1,64 |
4,47 |
4,24 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
4,98 |
7,81 |
4,55 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
3,34 |
0,51 |
5,61 |
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
∞ |
0 |
1,41 |
7 |
6,02 |
5,84 |
7,04 |
6,35 |
1,45 |
5,04 |
1,88 |
4,71 |
0 |
8 |
12,38 |
9,95 |
4,90 |
7,12 |
7,81 |
0,84 |
0 |
∞ |
2,27 |
В строке 7 и столбце 9 отсутствует элемент, равный ∞. Присвоим элементу (7,9) значение ∞, чтобы избежать преждевременного замыкания контура.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
7,30 |
10,13 |
7,67 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
4,47 |
7,30 |
7,07 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,47 |
4,57 |
9,67 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
1,64 |
4,47 |
4,24 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
4,98 |
7,81 |
4,55 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
3,34 |
0,51 |
5,61 |
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
∞ |
0 |
1,41 |
7 |
6,02 |
5,84 |
7,04 |
6,35 |
1,45 |
5,04 |
1,88 |
4,71 |
∞ |
8 |
12,38 |
9,95 |
4,90 |
7,12 |
7,81 |
0,84 |
0 |
∞ |
2,27 |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
9 |
Минимумы строк |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
7,30 |
10,13 |
7,67 |
|
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
4,47 |
7,30 |
7,07 |
|
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,47 |
4,57 |
9,67 |
|
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
1,64 |
4,47 |
4,24 |
|
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
4,98 |
7,81 |
4,55 |
|
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
3,34 |
0,51 |
5,61 |
|
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
∞ |
0 |
1,41 |
|
7 |
6,02 |
5,84 |
7,04 |
6,35 |
1,45 |
5,04 |
1,88 |
4,71 |
∞ |
1,45 |
8 |
12,38 |
9,95 |
4,90 |
7,12 |
7,81 |
0,84 |
0 |
∞ |
2,27 |
|
Находим минимальные элементы в каждой строке:
В данном случае ненулевой минимум будет только в строке 7. Вычитаем его из элементов этой строки.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
7,30 |
10,13 |
7,67 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
4,47 |
7,30 |
7,07 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,47 |
4,57 |
9,67 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
1,64 |
4,47 |
4,24 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
4,98 |
7,81 |
4,55 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
3,34 |
0,51 |
5,61 |
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
∞ |
0 |
1,41 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
3,59 |
0,43 |
3,26 |
∞ |
8 |
12,38 |
9,95 |
4,90 |
7,12 |
7,81 |
0,84 |
0 |
∞ |
2,27 |
То же проделываем и со столбцами.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
7,30 |
10,13 |
7,67 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
4,47 |
7,30 |
7,07 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,47 |
4,57 |
9,67 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
1,64 |
4,47 |
4,24 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
4,98 |
7,81 |
4,55 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
3,34 |
0,51 |
5,61 |
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
∞ |
0 |
1,41 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
3,59 |
0,43 |
3,26 |
∞ |
8 |
12,38 |
9,95 |
4,90 |
7,12 |
7,81 |
0,84 |
0 |
∞ |
2,27 |
Минимумы столбцов |
|
|
|
|
|
|
|
|
1,41 |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
7,30 |
10,13 |
6,26 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
4,47 |
7,30 |
5,66 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,47 |
4,57 |
8,26 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
1,64 |
4,47 |
2,83 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
4,98 |
7,81 |
3,14 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
3,34 |
0,51 |
4,20 |
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
∞ |
0 |
0 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
3,59 |
0,43 |
3,26 |
∞ |
8 |
12,38 |
9,95 |
4,90 |
7,12 |
7,81 |
0,84 |
0 |
∞ |
0,86 |
Находим: Г01=0,18+0=0,18; Г10=0+0,18=0,18; Г13=0+0=0;
Г14=0+0=0; Г23=0+0=0; Г25=0+0,33=0,33; Г31=0,33+0=0,33;
Г41=0,18+0=0,18; Г52=0,51+0,33=0,84; Г68=0+0,51=0,51;
Г69=0+0,86=0,86; Г74=0,43+0,18=0,61; Г86=0,84+0,43=1,27.
Максимальное значение Г86=1,27. Дуга 8-6 входит в маршрут.
Удаляем из матрицы строку 8 и столбец 6.
|
0 |
1 |
2 |
3 |
4 |
5 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
10,13 |
6,26 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
7,30 |
5,66 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,57 |
8,26 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
4,47 |
2,83 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
7,81 |
3,14 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
0,51 |
4,20 |
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
0 |
0 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
3,59 |
3,26 |
∞ |
В строке 6 и столбце 8 нет элемента ∞. Присваиваем элементу (6,8) значение ∞.
|
0 |
1 |
2 |
3 |
4 |
5 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
10,13 |
6,26 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
7,30 |
5,66 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,57 |
8,26 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
4,47 |
2,83 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
7,81 |
3,14 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
0,51 |
4,20 |
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
∞ |
0 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
3,59 |
3,26 |
∞ |
Минимумы столбцов |
|
|
|
|
|
|
0,51 |
|
Минимальные элементы всех строк равны 0, минимальный ненулевой элемент имеется в столбце 8 и равен 0,51.
|
0 |
1 |
2 |
3 |
4 |
5 |
8 |
9 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
9,62 |
6,26 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
6,79 |
5,66 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,06 |
8,26 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
3,96 |
2,83 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
7,30 |
3,14 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
0 |
4,20 |
6 |
9,55 |
7,43 |
2,33 |
5,49 |
4,98 |
0,33 |
∞ |
0 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
3,59 |
2,75 |
∞ |
Г01=0,18+0=0,18; Г10=0+0,18=0,18; Г13=0+0=0; Г14=0+0=0;
Г23=0+0=0; Г25=0+0,33=0,33; Г31=0,33+0=0,33; Г41=0,18+0=0,18;
Г52=0+0,33=0,33; Г58=0+2,75=2,75; Г69=0,33+2,83=5,58;
Г74=2,75+0=2,75.
Максимальное значение Г69=5,58. Дуга 6-9 входит в маршрут.
Удаляем из матрицы строку 6 и столбец 9.
|
0 |
1 |
2 |
3 |
4 |
5 |
8 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
9,62 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
6,79 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,06 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
3,96 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
7,30 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
0 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
3,59 |
2,75 |
В строке 7 и столбце 8 нет ∞. Присваиваем элементу (7,8) значение ∞.
|
0 |
1 |
2 |
3 |
4 |
5 |
8 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
9,62 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
6,79 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
4,06 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
3,96 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
7,30 |
5 |
7,88 |
5,05 |
0 |
2,22 |
4,67 |
∞ |
0 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
3,59 |
∞ |
Во всех строках и столбцах имеются нули. Поэтому находим
Г01=0,18+0=0,18; Г10=0+0,18=0,18; Г13=0+0=0; Г14=0+0=0;
Г23=0+0=0; Г25=0+3,49=3,49; Г31=0,33+0=0,33; Г41=0,18+0=0,18;
Г52=0+0,33=0,33; Г58=0+3,96=3,96; Г74=3,59+0=3,59.
Максимальное значение Г58=3,96. Дуга 5-8 входит в маршрут.
Удаляем из матрицы строку 5 и столбец 8.
|
0 |
1 |
2 |
3 |
4 |
5 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
3,59 |
В строке 7 и столбце 5 нет ∞. Присваиваем элементу (7,5) значение ∞.
|
0 |
1 |
2 |
3 |
4 |
5 |
0 |
∞ |
0 |
5,45 |
4,84 |
0,18 |
8,61 |
1 |
0 |
∞ |
3,16 |
0 |
0 |
6,32 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
3 |
2,83 |
0 |
0,33 |
∞ |
0,51 |
3,49 |
4 |
0,18 |
0 |
3,67 |
0,51 |
∞ |
5,00 |
7 |
4,57 |
4,39 |
5,59 |
4,90 |
0 |
∞ |
Минимумы столбцов |
|
|
0,33 |
|
|
|
В столбце 2 нет нулевых элементов и минимальное их значение равно 0,33. Вычитаем это значение из всех элементов этого столбца.
|
0 |
1 |
2 |
3 |
4 |
5 |
0 |
∞ |
0 |
5,12 |
4,84 |
0,18 |
8,61 |
1 |
0 |
∞ |
2,83 |
0 |
0 |
6,32 |
2 |
4,77 |
1,94 |
∞ |
0 |
3,34 |
0 |
3 |
2,83 |
0 |
0 |
∞ |
0,51 |
3,49 |
4 |
0,18 |
0 |
3,34 |
0,51 |
∞ |
5,00 |
7 |
4,57 |
4,39 |
5,26 |
4,90 |
0 |
∞ |
Г01=0,18+0=0,18; Г10=0+0,18=0,18; Г13=0+0=0; Г14=0+0=0;
Г23=0+0=0; Г25=0+3,49=3,49; Г31=0+0=0; Г32=0+2,83=2,83;
Г41=0,18+0=0,18; Г74=4,39+0=4,39.
Максимальное значение равно Г74=4,39. Дуга 7-4 входит в маршрут.
Удаляем из матрицы строку 7 и столбец 4.
|
0 |
1 |
2 |
3 |
5 |
0 |
∞ |
0 |
5,12 |
4,84 |
8,61 |
1 |
0 |
∞ |
2,83 |
0 |
6,32 |
2 |
4,77 |
1,94 |
∞ |
0 |
0 |
3 |
2,83 |
0 |
0 |
∞ |
3,49 |
4 |
0,18 |
0 |
3,34 |
0,51 |
5,00 |
|
0 |
1 |
2 |
3 |
5 |
0 |
∞ |
0 |
5,12 |
4,84 |
8,61 |
1 |
0 |
∞ |
2,83 |
0 |
6,32 |
2 |
4,77 |
1,94 |
∞ |
0 |
0 |
3 |
2,83 |
0 |
0 |
∞ |
3,49 |
4 |
0,18 |
0 |
3,34 |
0,51 |
∞ |
Во всех строках и столбцах имеются нули и поэтому никаких вычитаний не делаем и сразу вычисляем
Г01=4,84+0=4,84; Г10=0+0,18=0,18; Г13=0+0=0; Г23=0+0=0;
Г25=0+3,49=3,49; Г31=0+0=0; Г32=0+2,83=2,83; Г41=0,18+0=0,18.
Максимальное значение равно Г01=4,84. Дуга 0-1 входит в маршрут.
Удаляем из матрицы строку 0 и столбец 1.
|
0 |
2 |
3 |
5 |
1 |
0 |
2,83 |
0 |
6,32 |
2 |
4,77 |
∞ |
0 |
0 |
3 |
2,83 |
0 |
∞ |
3,49 |
4 |
0,18 |
3,34 |
0,51 |
∞ |
В строке 1 и столбце 0 нет ∞. Присваиваем элементу (1,0) значение ∞.
|
0 |
2 |
3 |
5 |
Минимумы строк |
1 |
∞ |
2,83 |
0 |
6,32 |
|
2 |
4,77 |
∞ |
0 |
0 |
|
3 |
2,83 |
0 |
∞ |
3,49 |
|
4 |
0,18 |
3,34 |
0,51 |
∞ |
0,18 |
В строке 4 минимальный ненулевой элемент равен 0,18. Вычитаем его из всех остальных элементов строки.
|
0 |
2 |
3 |
5 |
1 |
∞ |
2,83 |
0 |
6,32 |
2 |
4,77 |
∞ |
0 |
0 |
3 |
2,83 |
0 |
∞ |
3,49 |
4 |
0 |
3,16 |
0,33 |
∞ |
Во всех строках и столбцах имеются нули и поэтому сразу вычисляем:
Г13=2,83+0=2,83; Г23=0+0=0; Г25=0+3,49=3,49; Г32=2,83+2,83=5,66;
Г40=0,33+2,83=3,16.
Максимальное значение соответствует Г32=5,66. Дуга 3-2 входит в маршрут.
Удаляем из матрицы строку 3 и столбец 2.
|
0 |
3 |
5 |
1 |
∞ |
0 |
6,32 |
2 |
4,77 |
0 |
0 |
4 |
0 |
0,33 |
∞ |
В строке 2 и столбце 3 нет ∞. Присваиваем элементу (2,3) значение ∞.
|
0 |
3 |
5 |
1 |
∞ |
0 |
6,32 |
2 |
4,77 |
∞ |
0 |
4 |
0 |
0,33 |
∞ |
Во всех строках и столбцах – нули и потому вычисляем
Г13=6,32+0,33=6,65; Г25=4,77+6,32=11,09; Г40=0,33+4,77=5,10.
Максимальное значение равно Г25=11,09. Дуга 2-5 входит в маршрут.
Удаляем из матрицы строку 2 и столбец 5.
|
0 |
3 |
1 |
∞ |
0 |
4 |
0 |
0,33 |
Элемент (4,3) заменяем на ∞.
|
0 |
3 |
1 |
∞ |
0 |
4 |
0 |
∞ |
Расчет закончен. К уже найденному маршруту добавляем дуги 1-3, 4-0 (соответствуют нулевым элементам матрицы).
Выписываем все дуги маршрута:
(9-7), (8-6), (6-9), (5-8), (7-4), (0-1), (3-2), (2-5), (1-3), (4-0).
Получаем маршрут: 0-1-3-2-5-8-6-9-7-4-0.
Длина маршрута вычисляется как сумма вычтенных элементов:
3,16+2,83+3,16+2,83+3,61+3,61+2,83+2,24+2,83+2,24+0,33+0,78+0,45+1,45+
+1,41+0,51+0,33+0,18=34.78.

 --
-- =3
=3
 1,77
1,77