§ 6.6. Ускорение при плоском движении твердого тела1
Рис. 6.19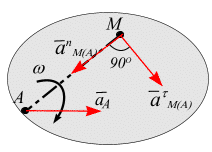
![]() и ускорения этой точки при вращательном
движении тела вокруг полюса (рис. 6.19):
и ускорения этой точки при вращательном
движении тела вокруг полюса (рис. 6.19):
![]() (6.5)
(6.5)
Здесь:
![]() – нормальное
ускорение точки М
во вращении вокруг полюса
;
– нормальное
ускорение точки М
во вращении вокруг полюса
;
![]() – касательное
ускорение точки М во вращении вокруг
полюса А.
– касательное
ускорение точки М во вращении вокруг
полюса А.
Рис. 6.20 |
Модуль и направление
ускорения точки М
–
|
П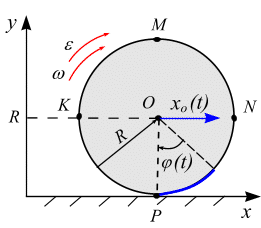 ример
6.2. Колесо
радиусом R
катится без скольжения по линейному
рельсу. Центр
ример
6.2. Колесо
радиусом R
катится без скольжения по линейному
рельсу. Центр
![]() колеса движется согласно уравнению
колеса движется согласно уравнению
![]() .
Вычислить в момент времени
.
Вычислить в момент времени
![]() ускорения точек Р,
М, К, N
расположенных на ободе колеса, как
показано на рис. 6.21.
ускорения точек Р,
М, К, N
расположенных на ободе колеса, как
показано на рис. 6.21.
Решение. За полюс выберем точку . Уравнения вращения колеса вокруг полюса имеет вид
Рис. 6.21 ![]() .
.
Вычислим угловую
скорость
![]() ,
угловое ускорение
и ускорение полюса. Имеем
,
угловое ускорение
и ускорение полюса. Имеем
![]()
Направление и показано дуговыми стрелками (рис. 6. 22).
Ускорение точки М вычислим по формуле
![]() .
.
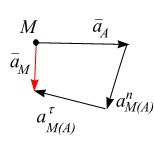
Приводим к точке
М
ускорение полюса
![]() ,
рис. 6.22, а. Для нормального и касательного
ускорений точки М
от вращения колеса вокруг полюса О
имеем,
рис.6.22, б:
,
рис. 6.22, а. Для нормального и касательного
ускорений точки М
от вращения колеса вокруг полюса О
имеем,
рис.6.22, б:
![]()
Ускорение
![]() направлено от точки М
к полюсу О.
Ускорение
направлено от точки М
к полюсу О.
Ускорение
![]() перпендикулярно отрезку ОМ
и направлено в сторону дуговой стрелки
.
перпендикулярно отрезку ОМ
и направлено в сторону дуговой стрелки
.
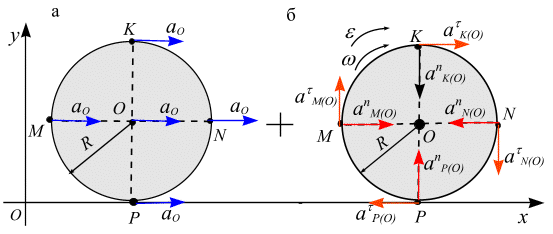
Рис. 6.22
Модуль ускорения в точке М:
![]()
Направление вектора показано на (рис. 6.23, а.).
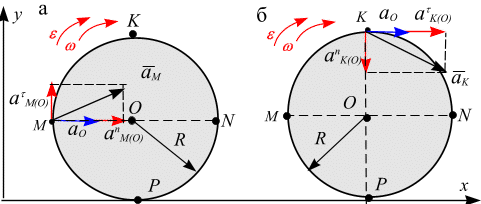
Рис. 6.23
Для точки
![]() имеем (рис. 6.23, б):
имеем (рис. 6.23, б):
![]() .
.
Направление вектора
![]() показано
на рис. 6.23, б
показано
на рис. 6.23, б
Для точки N имеем
![]() .
.
Направление вектора показано на рис. 6.24, а.
Для точки Р имеем:
![]() .
.
Направление вектора
![]() показано
на рис.6.24, б.
показано
на рис.6.24, б.
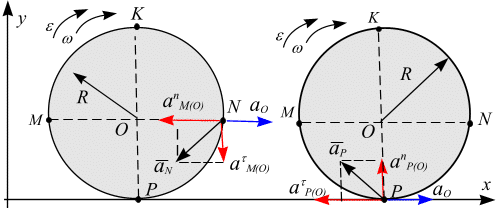
Рис. 6.24
§.6.7. Основные способы вычисления углового ускорения
при плоском движении
При вычислении ускорения точек тела при его плоском движении, необходимо знать, согласно (6.5), ускорение полюса, угловую скорость и угловое ускорение . Ускорение полюса должно быть известно по определению. Угловую скорость обычно вычисляют, используя общую теорему кинематики или свойства мгновенного центра скоростей. Сложность заключается в вычислении углового ускорения .
Рассмотрим примеры вычисления углового ускорения.
Заданы уравнения плоского движения тела
Тогда угловое ускорение
![]() .
.
Пример вычисления ускорений точек твердого тела, когда заданы уравнения плоского движения, рассмотрен в примере 6.2. на стр. 134.
Вычисление углового ускорения, если направление ускорения в исследуемой точке известно
Рассмотрим кривошипно-шатунный механизм, рис. 6.25.
Кривошип вращается
с угловой скоростью![]() и угловым ускорением
и угловым ускорением
![]() ускоренно. Рассмотрим, как вычисляется
угл
ускоренно. Рассмотрим, как вычисляется
угл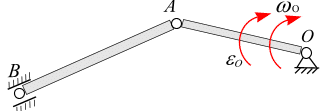 овая
скорость и угловое ускорение шатуна
АВ.
овая
скорость и угловое ускорение шатуна
АВ.
1). На шатуне АВ
Рис.
6.25 нужно выбрать полюс, т.е. точку,
скорость и ускорение которой известно.
Точка А
одновременно принадлежит и шатуну АВ
и кривошипу
![]() .
Точка А
по отношению к точке О
перемещается по окружности радиусом
ОА.
Совместим оси естественного трехгранника
.
Точка А
по отношению к точке О
перемещается по окружности радиусом
ОА.
Совместим оси естественного трехгранника
![]() с тоской А,
рис. 6.26. Вычислим скорость и ускорение
точки А
кривошипа
:
с тоской А,
рис. 6.26. Вычислим скорость и ускорение
точки А
кривошипа
:
![]() (м/с),
(м/с),
![]() ,
,
![]() ,
,
![]()
Вектор скорости
и вектор
![]() направлены по оси
направлены по оси
![]() ,
вектор
,
вектор
![]() направлен по оси
направлен по оси
![]() (рис. 6.26).
(рис. 6.26).
Свяжем декартову
систему координат
![]() с
ползуном В,
рис. 6.26. Ползун В
движется
поступательно вдоль дорожек.
с
ползуном В,
рис. 6.26. Ползун В
движется
поступательно вдоль дорожек.
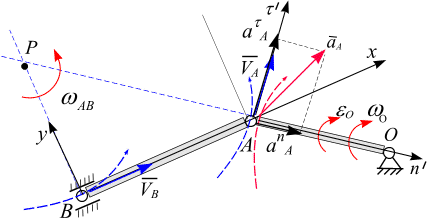
Рис. 6.26
Вектор скорости
ползуна
направлен по оси
![]() .
Скорости в точках А
и В
шатуна АВ не
параллельны, следовательно шатун
совершает плоскопараллельное движение.
Восстановим
перпендикуляры к векторам
и
.
Точка МЦС (точка Р)
лежит на их пересечении. Все точки шатуна
мгновенно движутся по окружностям
соответствующих радиусов с центром в
точке МЦС (точка А – по радиусу
,
точка В
– по радиусу
,
при этом угловая
скорость вращения шатуна и модули
скоростей точек шатуна связаны
соотношением:
.
Скорости в точках А
и В
шатуна АВ не
параллельны, следовательно шатун
совершает плоскопараллельное движение.
Восстановим
перпендикуляры к векторам
и
.
Точка МЦС (точка Р)
лежит на их пересечении. Все точки шатуна
мгновенно движутся по окружностям
соответствующих радиусов с центром в
точке МЦС (точка А – по радиусу
,
точка В
– по радиусу
,
при этом угловая
скорость вращения шатуна и модули
скоростей точек шатуна связаны
соотношением:
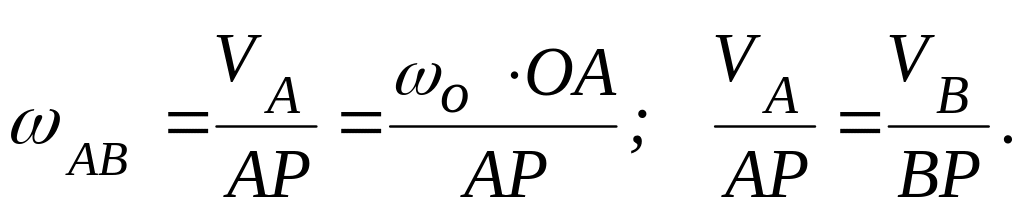
Скорость ползуна (скорость в точке В):
.
Вектор скорости ползуна направлен вдоль дорожек в сторону вращения шатуна (рис. 6.26).
2). Вычислим угловое
ускорение
![]() шатуна АВ.
Свяжем с точкой
шатуна АВ.
Свяжем с точкой
![]() оси
естественного трехгранника
оси
естественного трехгранника
![]() ,
рис. 6.27. Оси
соответственно совпали с осями
.
,
рис. 6.27. Оси
соответственно совпали с осями
.
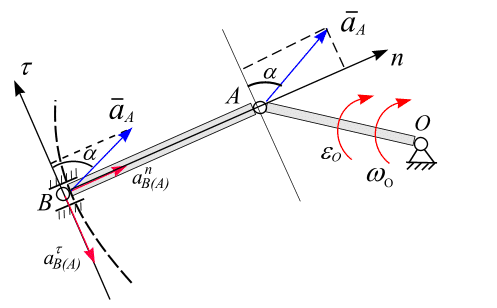
Рис.6.27
Ускорение точки В:
![]() ,
(а)
,
(а)
здесь:
![]() –
ускорение полюса
А;
–
ускорение полюса
А;
![]() –
касательное
ускорение точки В
при ее
вращении вокруг полюса А;
–
касательное
ускорение точки В
при ее
вращении вокруг полюса А;
![]() –
нормальное ускорение
точки В при
ее вращении вокруг полюса А.
–
нормальное ускорение
точки В при
ее вращении вокруг полюса А.
Ползун В
движется прямолинейно по оси
![]() ,
следовательно вектор ускорения
,
следовательно вектор ускорения
![]() направлен
вдоль этой оси,
см. рис. 6.28.
Тогда, проекция векторного уравнения
(а) на ось
направлен
вдоль этой оси,
см. рис. 6.28.
Тогда, проекция векторного уравнения
(а) на ось
![]() будет равна нулю:
будет равна нулю:
![]()
откуда
Р |
Угловое ускорение
ползуна можно вычислить геометрически.
Для этого построим векторный
многоугольник из векторов
|
Из конца этого
вектора в том же масштабе, параллельно
оси
,
откладываем нормальную составляющую
ускорения
![]() ,
и из его конца проводим пунктирную
прямую -,
перпендикулярную
(неизвестное ускорение
,
и из его конца проводим пунктирную
прямую -,
перпендикулярную
(неизвестное ускорение
![]() лежит
на этой прямой) до пересечения с оью
.
Замыкающая
векторного многоугольника соответствует
вектору
.
лежит
на этой прямой) до пересечения с оью
.
Замыкающая
векторного многоугольника соответствует
вектору
.
Вычисление углового ускорения, если направление ускорения в исследуемой точке неизвестно.
Аналитически эти вычисления делают следующим образом.
Рассмотрим механизм
ОАВС.
Вычислим угловое ускорение звена
![]() и звена
и звена
![]() ,
если угловая скорость ведущего звена
ОА
постоянна и равна
,
если угловая скорость ведущего звена
ОА
постоянна и равна
![]() (рис. 6.29, а). Пусть кривошип
(рис. 6.29, а). Пусть кривошип
![]() см
вращается равномерно относительно
центра О
с угловой скоростью
см
вращается равномерно относительно
центра О
с угловой скоростью
![]() ;
длины звеньев
;
длины звеньев
![]() см,
см,
![]() см.
см.
Вычислим угловые
скорости звеньев
![]()
![]() и
и
![]()
![]() .Для
этого вычислим скорость точка А
кривошипа ОА:
.Для
этого вычислим скорость точка А
кривошипа ОА:
![]()
Направлен вектор скорости перпендикулярно .
Точка В принадлежит
кривошипу ВС, следовательно вектор
скорости
![]() будет направлен перпендикулярно
ВС.
будет направлен перпендикулярно
ВС.
а |
|
б |
|
Рис. 6.29 |
|||
Скорости в точках А и В шатуна АВ не параллельны, следовательно шатун совершает плоскопараллельное движение. Восстановим перпендикуляры к векторам и . Точка МЦС (точка Р) лежит на их пересечении. Все точки шатуна мгновенно движутся по окружностям соответствующих радиусов с центром в точке МЦС (точка А – по радиусу , точка В – по радиусу ), при этом угловая скорость вращения шатуна и модули скоростей точек шатуна связаны соотношением:
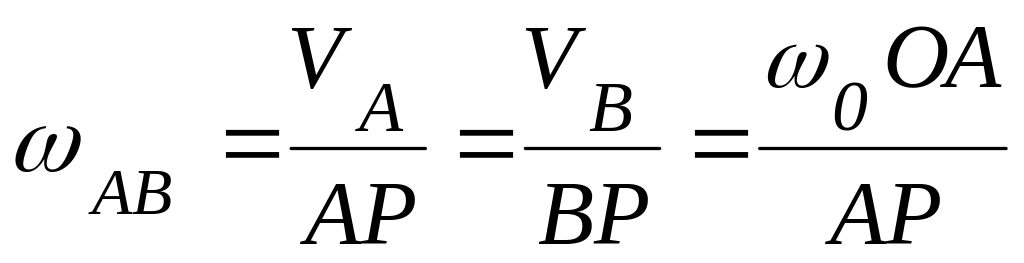
![]()
Из
![]() вычисляем:
вычисляем:
![]() см;
см;
![]() см.
см.
Тогда
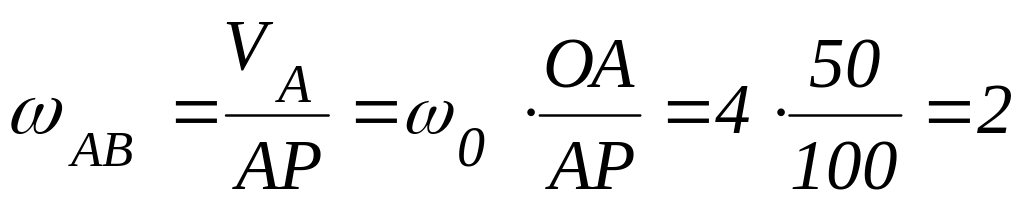 (с-1);
(с-1);
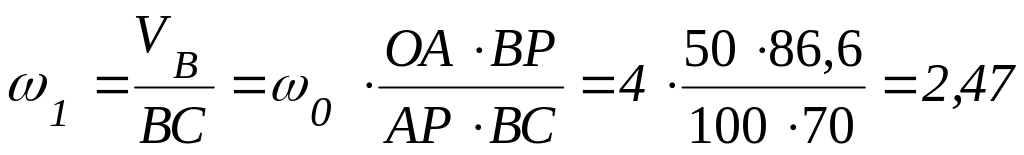 (с-1).
(с-1).
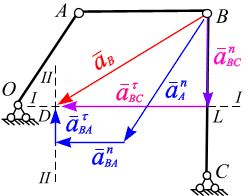
Аналитический способ вычисление углового ускорения
Применим теорему об ускорениях при плоском движении тела к точке В. За полюс выбираем точку А, ускорение в этой точке известно, рис. 6.31:
![]() (см/с2);
(см/с2);
тогда |
|
(а) |
здесь
![]() (см/с2);
(см/с2);
![]()
В полученном
векторном уравнении (а) три неизвестных:
модуль и направление ускорения в точке
В
![]() и угловое ускорение шатуна АВ
и угловое ускорение шатуна АВ ![]() (
(![]() ).
).
Для решения задачи необходимо записать еще одно уравнение.
За второй полюс
выберем точку
,
![]() ,
тогда (рис. 6.30):
,
тогда (рис. 6.30):
![]() (б)
(б)
Здесь
![]() (см/с2);
(см/с2);
![]()
В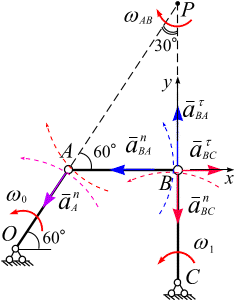 полученном векторном равенстве (б) тоже
три неизвестных: модуль и направление
ускорения в точке В
и угловое ускорение кривошипа
полученном векторном равенстве (б) тоже
три неизвестных: модуль и направление
ускорения в точке В
и угловое ускорение кривошипа
![]()
![]() .
(
.
(![]() ).
).
Получили систему уравнений, которая содержит шесть неизвестных:
![]() (в)
(в)
Рис. 6.30 Исключим
вектор
![]() из (в), тем самым
из (в), тем самым
исключим две
неизвестные из (в). Для этого приравняем
правые части уравнений (в) между собой,
получим векторное уравнение, которое
будет содержать только две неизвестные
величины:
![]() и
:
и
:
![]() . (г)
. (г)
Р |
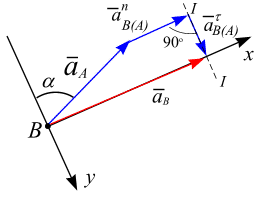
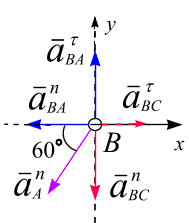
Совместим с точкой В начало декартовой системы координат (рис. 6.31). Приведем к точке В векторы (г) и спроецируем их на оси , рис. 6.32:
|
Получили систему
двух скалярных уравнений с двумя
неизвестными:
![]() и
и
![]() .
Решая о систему уравнений (1), получим:
.
Решая о систему уравнений (1), получим:
![]()
![]() Знак
()
модуля
Знак
()
модуля
![]() показывает, что истинное направление
этого вектора противоположно выбранному
на схеме (рис. 6.31).
показывает, что истинное направление
этого вектора противоположно выбранному
на схеме (рис. 6.31).
![]()
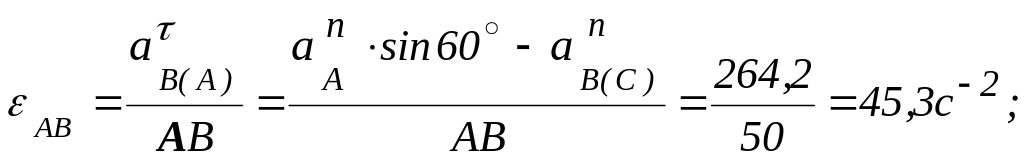
![]()
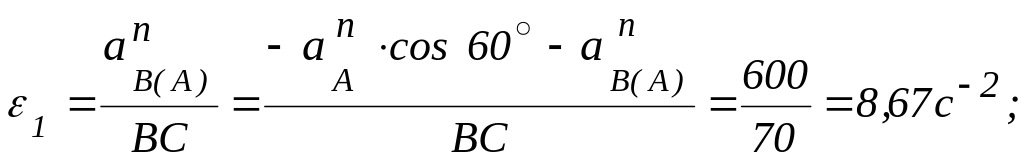
Графический (геометрический) способ
Ускорение шарнира В получим построением многоугольника ускорений (рис. 6.32). Рассмотрим векторное равенство (г):
![]() ,
,
здесь
![]() (см/с2),
(см/с2),
![]() (см/с2),
(см/с2),
![]() (см/с2).
(см/с2).
Рис. 6.32 |
В выбранном
масштабе откладываем из точки В,
параллельно ОА,
ускорение
|
пунктирную прямую
-,
перпендикулярную
(ускорение
лежит
на этой прямой).Затем из точки В,
в том же масштабе, откладываем нормальную
составляющую ускорения
![]()
вдоль звена ВС,
из конца этого вектора проводим
перпендикулярную ему пунктирную прямую
-
(, ускорение
вдоль звена ВС,
из конца этого вектора проводим
перпендикулярную ему пунктирную прямую
-
(, ускорение
![]() лежит на этой прямой), см. рис. 6.32.
лежит на этой прямой), см. рис. 6.32.
Обозначим точку
пересечения прямых -
и -
буквой D.
Соединим точку В
и точку D,
полученная прямая
![]() соответствует ускорению точки В
соответствует ускорению точки В
![]() ;
прямая
;
прямая
![]() соответствует ускорению
;
прямая
соответствует ускорению
;
прямая
![]() соответствует ускорению
.
Замеряем длину отрезков, с учетом
принятого масштаба, получаем:
соответствует ускорению
.
Замеряем длину отрезков, с учетом
принятого масштаба, получаем:
![]() (см/с2);
(см/с2);
![]() (см/с2);
(см/с2);
Результаты получены двумя разными способами, хорошо согласуются друг с другом.
1 Для самостоятельного изучения

 ис.
6.28
ис.
6.28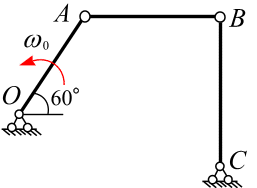

 ис.
6.31
ис.
6.31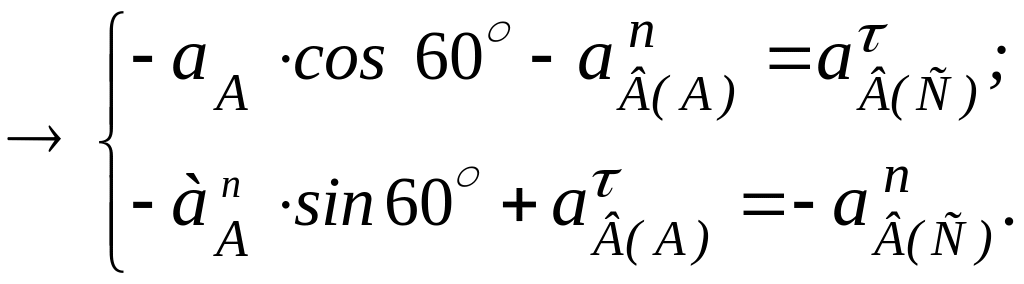 (1)
(1)