
§ 6.4. Частные случаи нахождения точки мцс
Рассмотрим частные случаи нахождения точки МЦС.
Если плоское движение осуществляется путем качения цилиндрического тела по поверхности другого тела без скольжения, причем второе тело неподвижно, то точка касания Р имеет в данный момент времени скорость, равную нулю, следовательно, является МЦС (рис. 6.13, а), тело мгновенно вращается относительно точки касания Р.
Иначе говоря, Если на перпендикуляре к вектору скорости есть точка, скорость в которой равна нулю, то эта точка будет точкой МЦС.
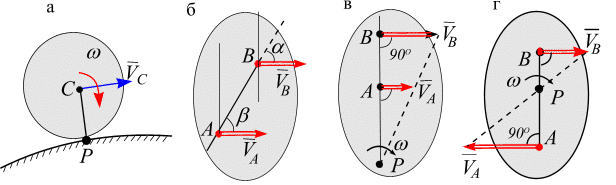
Рис. 6.13
Если в двух точках А и В твердого тела
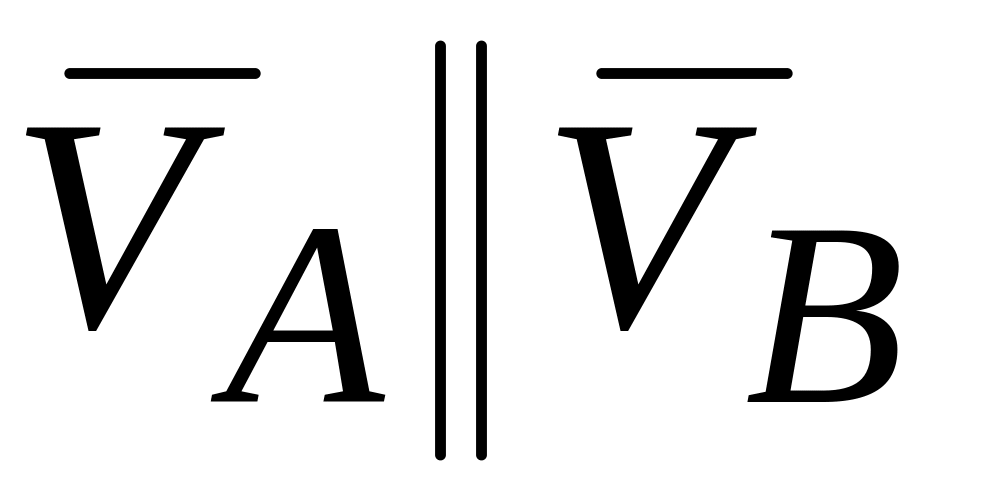 ,
при этом прямая
АВ, соединяющая
эти точки, не перпендикулярна векторам
и
,
при этом прямая
АВ, соединяющая
эти точки, не перпендикулярна векторам
и
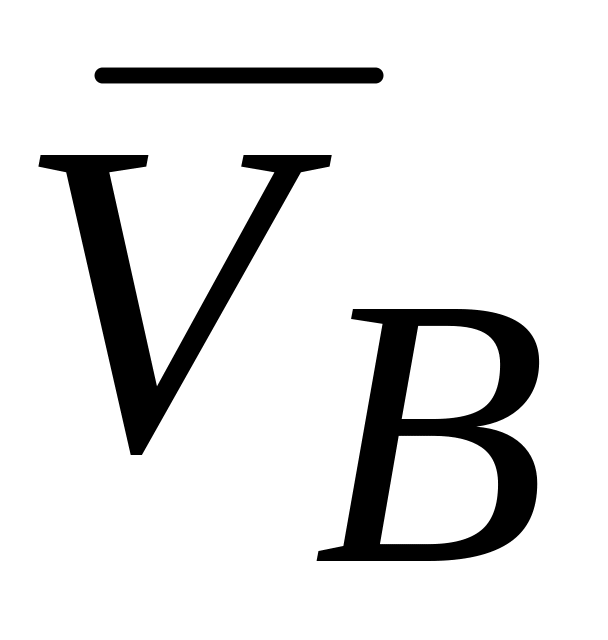 (рис. 6.13, б), то перпендикуляры к
и к
пересекутся в в бесконечности, т.е.
точка МЦС
(рис. 6.13, б), то перпендикуляры к
и к
пересекутся в в бесконечности, т.е.
точка МЦС
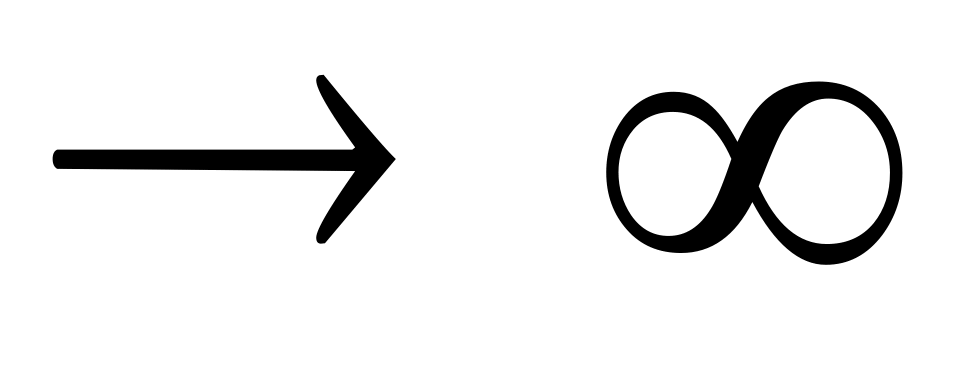 ,
тогда
,
тогда
 Из общей теоремы кинематики имеем, что
Из общей теоремы кинематики имеем, что
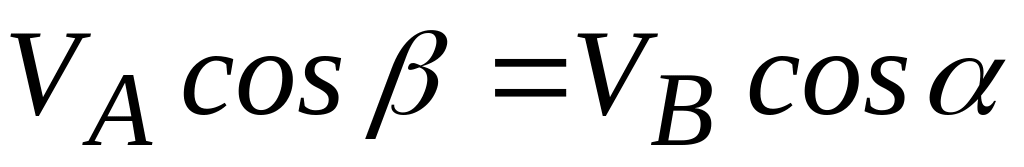 (
( ),
тогда
),
тогда
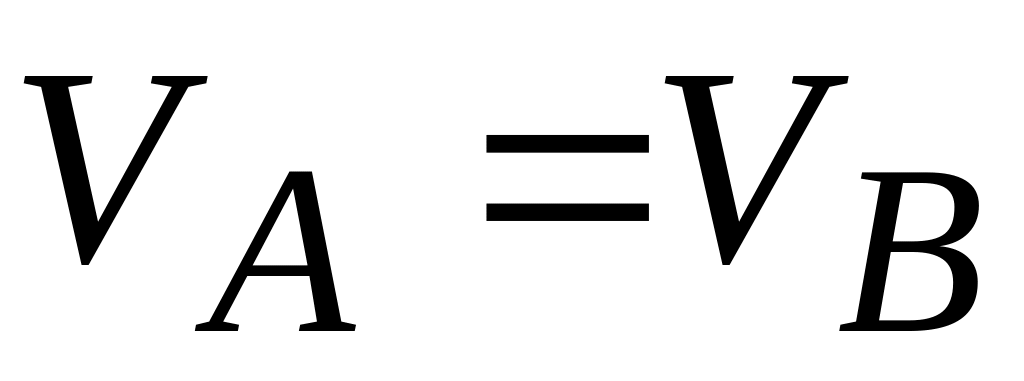 .
Следовательно, скорости всех точек
тела в данный момент равны между собой
по модулю и по направлению, твердое
тело движется мгновенно
поступательно. При
мгновенно
поступательном движении угловая
скорость тела равна нулю, угловое
ускорение не всегда равно нулю.
.
Следовательно, скорости всех точек
тела в данный момент равны между собой
по модулю и по направлению, твердое
тело движется мгновенно
поступательно. При
мгновенно
поступательном движении угловая
скорость тела равна нулю, угловое
ускорение не всегда равно нулю.
Если в двух точках А и В твердого тела , при этом прямая АВ, соединяющая эти точки, перпендикулярна векторам и и
 ,
,
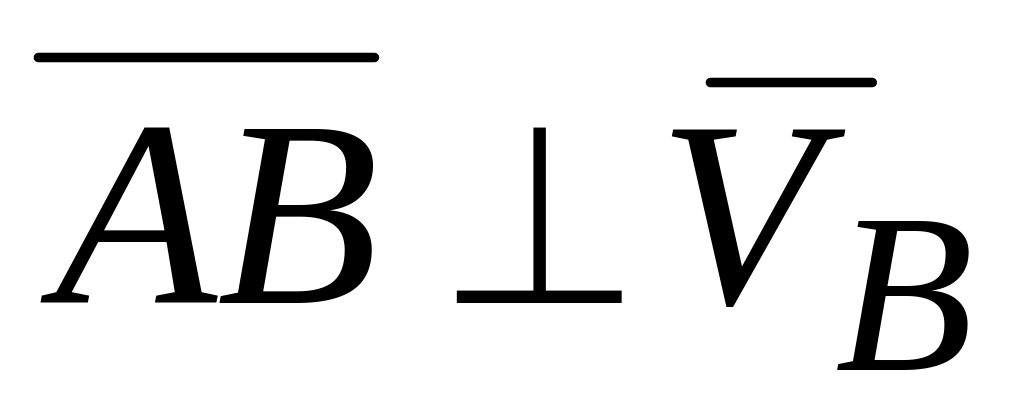 (рис. 6.13, в, г) то положение точки МЦС
определяется построениями, показанными
на рис. 6.13 в, г, тело имеет мгновенно-вращательное
движение вокруг
точки МЦС
(точка
Р). При этом
модули скоростей точек тела связаны
соотношением
(рис. 6.13, в, г) то положение точки МЦС
определяется построениями, показанными
на рис. 6.13 в, г, тело имеет мгновенно-вращательное
движение вокруг
точки МЦС
(точка
Р). При этом
модули скоростей точек тела связаны
соотношением
![]() .
.
§ 6.5. Механизмы
Р |
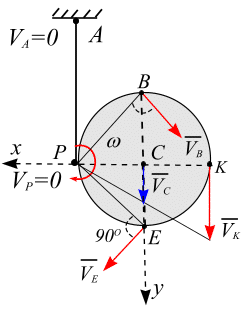
Маятник
Максвелла. Маятник
Максвелла состоит из диска радиусом
Свяжем декартову
систему координат
|
Следовательно, точка Р является точкой МЦС. Модули скоростей точек диска связаны соотношением
![]() .
.
Кривошипно – шатунный механизм. Кривошипно – шатунный механизм состоит из кривошипа ОА, шатуна АВ и ползуна В (рис. 6.15).
Р |
Кривошип ОА
длиной
Совместим
декартову систему координат с точкой
О.
Вычислим скорость ползуна
Имеем: |
![]() (м/с).
(м/с).
Вектор скорости
направлен перпендикулярно ОА
в сторону вращения кривошипа (рис. 6.15).
Ползун В
движется
поступательно вдоль дорожек, следовательно
скорость ползуна
![]() направлена по оси
направлена по оси
![]() .
Скорости в точках А
и В
шатуна АВ не
параллельны, следовательно шатун
совершает плоскопараллельное движение.
Восстановим
перпендикуляры к векторам
.
Скорости в точках А
и В
шатуна АВ не
параллельны, следовательно шатун
совершает плоскопараллельное движение.
Восстановим
перпендикуляры к векторам
![]() и
.
Точка МЦС (точка Р)
лежит на их пересечении
(рис. 6.15). Все
точки шатуна мгновенно движутся по
окружностям соответствующих радиусов
с центром вращения в точке МЦС (точка А
– по радиусу
,
точка В
– по радиусу
и
.
Точка МЦС (точка Р)
лежит на их пересечении
(рис. 6.15). Все
точки шатуна мгновенно движутся по
окружностям соответствующих радиусов
с центром вращения в точке МЦС (точка А
– по радиусу
,
точка В
– по радиусу
![]() ,
при этом угловая
скорость вращения шатуна и модули
скоростей точек шатуна связаны
соотношением:
,
при этом угловая
скорость вращения шатуна и модули
скоростей точек шатуна связаны
соотношением:
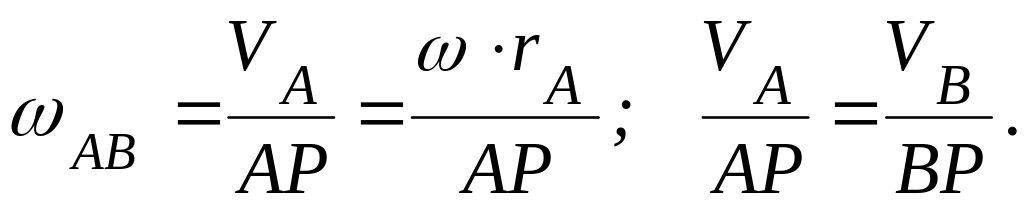
Скорость ползуна (скорость в точке В):
![]() .
.
Рассмотрим частные случаи.
Движение шатуна в момент времени, когда угол
 (рис.
6.16, а).
(рис.
6.16, а).
Вектор скорости
кривошипа в точке А
(![]() )
направлен по оси
)
направлен по оси
![]() .
Восстановим перпендикуляры к векторам
и
.
Точка МЦС (точка Р)
лежит на их пересечении и совпадает с
точкой В.
Следовательно, точка В
является в этом положении механизма
точкой МЦС, тогда
.
Восстановим перпендикуляры к векторам
и
.
Точка МЦС (точка Р)
лежит на их пересечении и совпадает с
точкой В.
Следовательно, точка В
является в этом положении механизма
точкой МЦС, тогда
![]() .
В этом положении шатун АВ
совершает мгновенное
вращение
вокруг мгновенно неподвижной точки В
с угловой скоростью
.
В этом положении шатун АВ
совершает мгновенное
вращение
вокруг мгновенно неподвижной точки В
с угловой скоростью
![]() :
:
![]() .
.
Распределение скоростей точек шатуна показано на рис. 6.16, а.
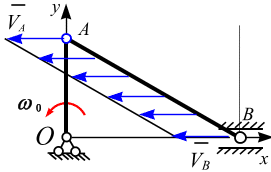
Движение шатуна в момент времени, когда угол
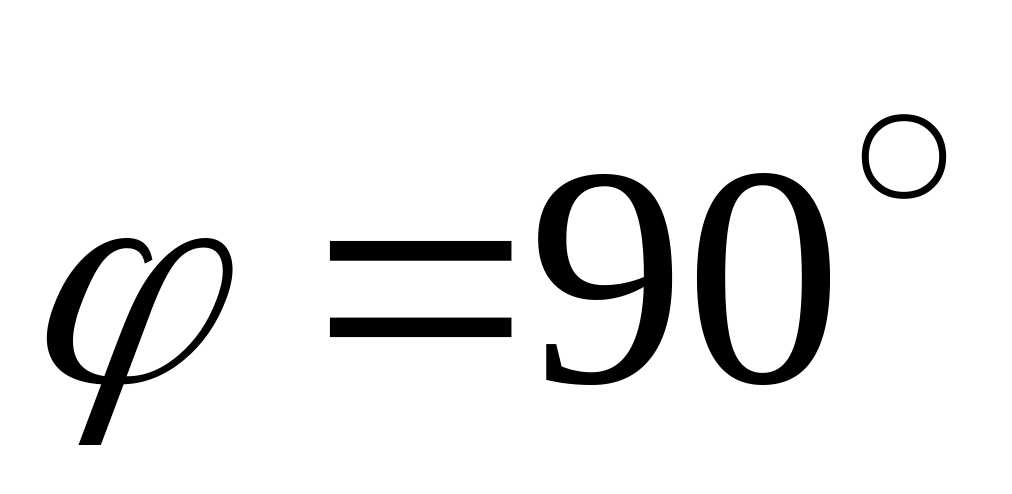 (рис. 6.16, б).
(рис. 6.16, б).
а |
|
б |
|
Рис. 6.16 |
|||
Вектор скорости
кривошипа в точке А
(
)
направлен по оси
.
Скорости
и
направлены параллельно друг другу,
перпендикуляры к
и
пересекутся в бесконечности, т.е. точка
МЦС
,
тогда
Следовательно, в этом положении шатун
совершает мгновенно-поступательное
движение, и все точки шатуна АВ
имеют одинаковую скорость, равную
![]() .
.
Р |
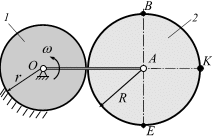
Планетарный
механизм. Планетарный
механизм состоит из неподвижного
диска 1
радиусом
,
кривошипа ОА
и подвижного диска, радиусом
,
закрепленного а точке
кривошипа
|
Кривошип ОА
вращается с угловой скоростью
и приводит в движение подвижный диск
2.
Вычислим скорость в точках
![]() ,
лежащие на ободе подвижного диска.
,
лежащие на ободе подвижного диска.
Имеем (рис. 6.18):
![]() .
.
Свяжем декартову
систему координат
![]() с
центром неподвижного диска. Скорость
в точке А
кривошипа параллельна оси
.
Точка соприкосновения неподвижного и
подвижного дисков будет точкой МЦС
точка
Р (рис.
6.18).
с
центром неподвижного диска. Скорость
в точке А
кривошипа параллельна оси
.
Точка соприкосновения неподвижного и
подвижного дисков будет точкой МЦС
точка
Р (рис.
6.18).
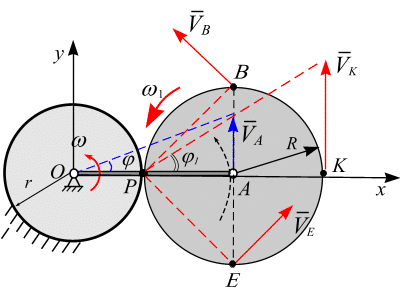
Рис. 6.18
Запишем уравнения
связи. Точка А
имеет два радиуса вращения –
![]() и
,
поэтому
и
,
поэтому
![]()
![]()
![]() .
.
При этом модули скоростей точек, лежащих на ободе подвижного диска связаны соотношением
![]() .
.
Подвижный диск движется плоскопараллельно.

 ис.
6.14
ис.
6.14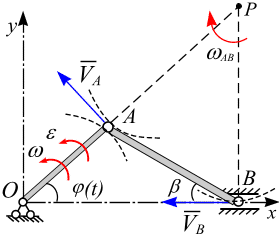 ис.
6.15
ис.
6.15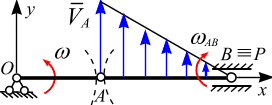
 ис.
6.17
ис.
6.17