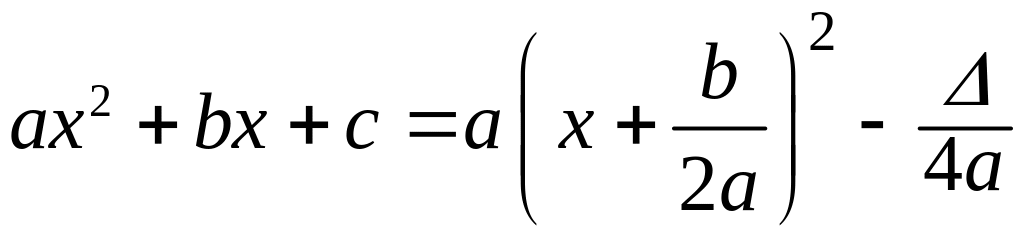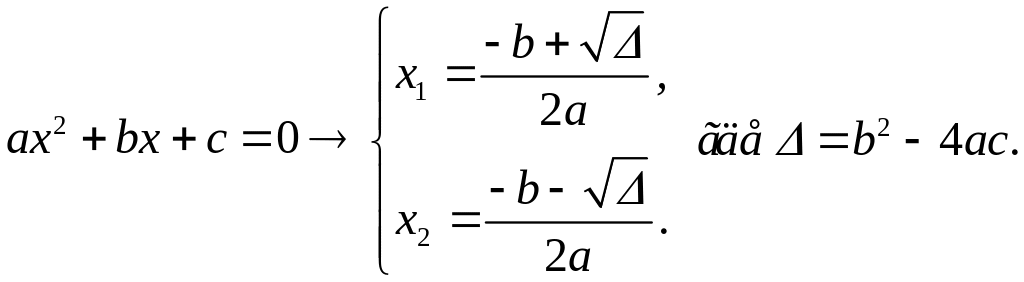- •Модуль I
- •§ 1. Введение
- •Общие методические указания
- •§ 1.1 Прямоугольная декартова система координат
- •§ 1.2. Графики аналитических функций в декартовой системе координат
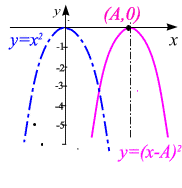
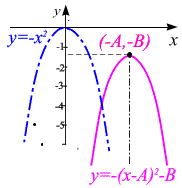
- •Квадратичная функция :
- •§ 1.3. Элементы тригонометрии
- •Графики тригонометрических функций
- •График функции представлен на рис. 1.9; это кривая называется также синусоида, полученная в результате перемещения графика вдоль оси влево на /2.
- •§ 1.4. Векторы
- •§ 1.5. Радиус–вектор
- •§ 1.6. Основы математического анализа
- •Правила интегрирования
- •§ 1.7. Понятие об абсолютно твердом теле и его степенях свободы
- •§ 1.8. Инерциальная система отсчета
§ 1.2. Графики аналитических функций в декартовой системе координат
Элементарные функции – функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
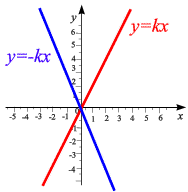
1. Линейная функция. Если переменные y и x пропорциональны, то функциональная зависимость между ними выражается уравнением:
![]() ,
,
где k – постоянная величина ( коэффициент пропорциональности ).
График
прямой пропорциональности – прямая
линия, проходящая через начало координат
и образующая с осью
![]() угол
угол
![]() ,
причем
,
причем
![]() –
коэффициент пропорциональности или
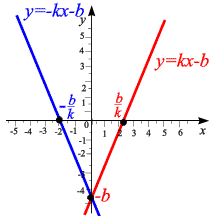
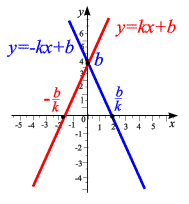
угловой коэффициент. На рис. 1.4
показаны графики линейный функций.
–
коэффициент пропорциональности или
угловой коэффициент. На рис. 1.4
показаны графики линейный функций.
|
|
|
Рис. 1.4 |
||
Квадратичная функция :
Выделение полного квадрата. Многочлен второй степени в множестве действительных чисел от одного аргумента имеет вид
![]() (1.1)
(1.1)
где
![]() ,
если
,
если
![]() то многочлен не является многочленом
второй степени.
то многочлен не является многочленом
второй степени.
При исследовании многочлена второй степени широко используется преобразование выделения полного квадрата из (1.1).
Имеем формулу сокращенного умножения:
![]() (1.2)
(1.2)
Сравним многочлены (1) и (2),
![]() и
и
![]()
и придадим форму (2) многочлену (1), т. е. выделим полный квадрат из многочлена (1):
Вынесем
сомножитель
![]() за
скобки, получим
за
скобки, получим
![]() .
(1.1’)
.
(1.1’)
Выражение
в скобках не содержит цифру 2 в произведении
аргументов
![]() и
и
![]() ,
и не содержит квадрата второго аргумента
,
и не содержит квадрата второго аргумента
![]() .
Следовательно, второе слагаемое в (1’)
помножим и поделим на 2, и добавим и
вычтем квадрат второго аргумента
,
получим
.
Следовательно, второе слагаемое в (1’)
помножим и поделим на 2, и добавим и
вычтем квадрат второго аргумента
,
получим
 . (1.2’)
. (1.2’)
Первые три слагаемых в квадратной скобке (2’) соответствуют формуле сокращенного умножения (2), следовательно, квадратную скобку можно записать как сумму двух слагаемых, получим
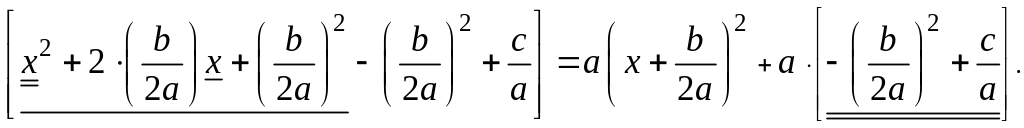 (1.2”)
(1.2”)
Преобразуем:
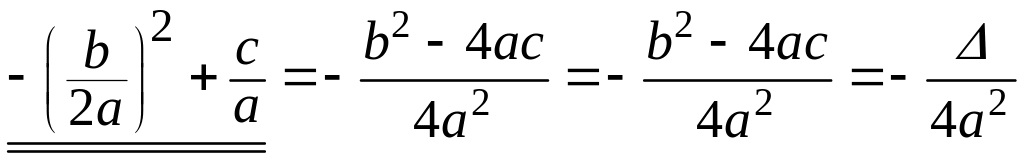 ,
где
,
где
![]() называется дискриминантом
многочлена второй степени от одного
аргумента. Выражение (2”) примет вид
называется дискриминантом
многочлена второй степени от одного
аргумента. Выражение (2”) примет вид
 .
.
Итак, процедура выделения полного квадрата привела к выражению:
|
Корни
квадратного уравнения. Корни
квадратичного
трехчлена
определяют
значения аргумента
![]() ,
при которых значение квадратичного
трехчлена равно нулю
,
при которых значение квадратичного
трехчлена равно нулю
![]() . (1.3)
. (1.3)
Выражение (3) принято называть квадратным уравнением. Вычислим корни квадратного уравнения.
Из
тождества
 следует, что корнями трехчлена являются
те значения
,
при которых
следует, что корнями трехчлена являются
те значения
,
при которых
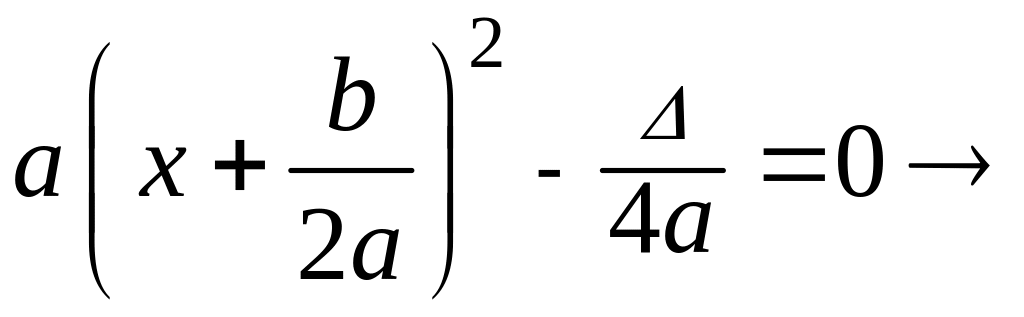
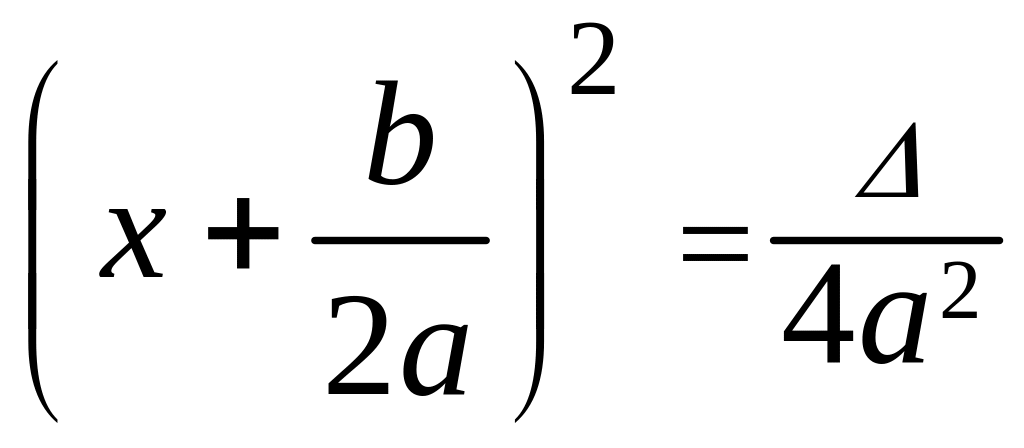 . (1.3’)
. (1.3’)
Решим (3) относительно , получим:
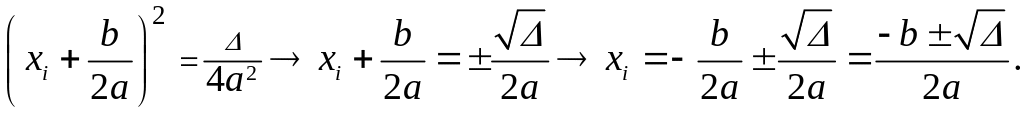
Здесь
![]() – дискриминант
многочлена второй степени.
– дискриминант
многочлена второй степени.
Получили, что квадратичное уравнение имеет два различных действительных корня:
|
Квадратичное уравнение:
– имеет
два действительных корня
![]() ,
если дискриминант положителен, т. е.
,
если дискриминант положителен, т. е.
![]() ;
;
– имеет
двукратный корень
![]() ,
если дискриминант равен нулю,
,
если дискриминант равен нулю,
т.
е.
![]() :
:
– не
имеет корней, если дискриминант
отрицательный, т. е.
![]()
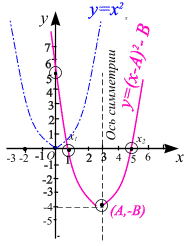
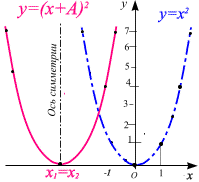
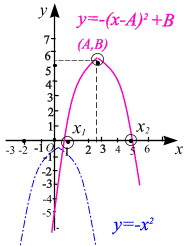
График квадратичной функции - парабола.
Свойства функции и вид её графика определяются, в основном, значениями коэффициента a и дискриминанта (рис. 1.5).
a
> 0,
|
a
> 0,
|
a
> 0,
|
|
|
|
a < 0, |
a < 0, |
a < 0, |
|
|
|
Рис. 1.5
Разложение на линейные множители:
при
![]() y
= ax2
+ bx
+ c = a(x
- x1)(x
- x2);
y
= ax2
+ bx
+ c = a(x
- x1)(x
- x2);
при
![]() y
= ax2
+ bx
+ c = a(x
- x1)2;
y
= ax2
+ bx
+ c = a(x
- x1)2;
при
![]() разложить на множители нельзя.
разложить на множители нельзя.
.
Квадратичная функциональная зависимость. Алгебраическая функция вида:
![]() ,
,
где А,B,C,D,E,F — действительные числа, называется функциональной зависимостью второй степени (порядка) или квадратичной функциональной зависимостью (кривые второго порядка). Графиками этой зависимости во множестве действительных чисел может быть окружность, эллипс, парабола, гипербола.
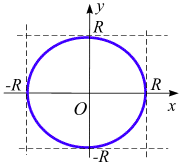
Окружность. Каноническое (простейшие) уравнение окружности (рис. 1.6 а):
![]() ;
;
параметрическое уравнение окружности:
![]()
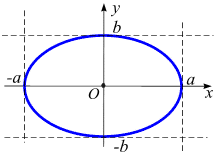
Эллипс. Каноническое уравнение эллипса (рис. 1.6 б):
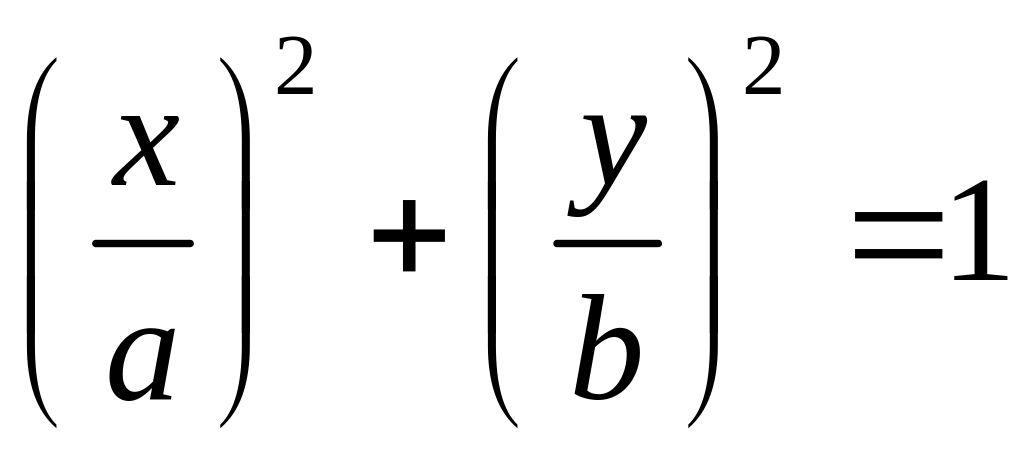 .
.
параметрическое уравнение эллипса:
![]()
-
а
б
в
г
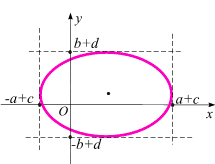
Рис. 1.6
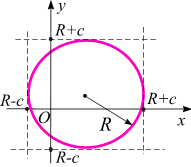
Уравнение окружности и эллипса со смещенными осями соответственно имеют вид (рис. 1.6, в, г):
![]() ;
;
 .
.
Параметрическое задание окружности и эллипса со смещенными осями имеют вид:
![]()