§ 5.5. Примеры решения задач
Пример 5.2. В примере 5.1. вычислить абсолютное ускорение.
Решение. Рассмотрим стержень, который вращается в плоскости вокруг неподвижного центра с угловой скоростью . Точка М скользит вдоль стержня со скоростью , рис. 5.6.
Рис. 5.6 |
Абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса.
. Здесь: |
– вектор относительного ускорения
,
т.к.
;
– вектор переносного ускорения
,
где
,
.
Вектор
направлен по оси
;
– ускорение Кориолиса
Определим направление вектора
,
используя правило Жуковского. Угол
между вектором относительной скорости
и
равен
(вектор
),
тогда вектор
разворачиваем
на
по
направлению дуговой
стрелки
(рис.
5.6).
Вычислим абсолютное ускорение точки :
Угол
между
и осью
равен.
,
.
Пусть , , ,
тогда
,
,
Рис. 5.7
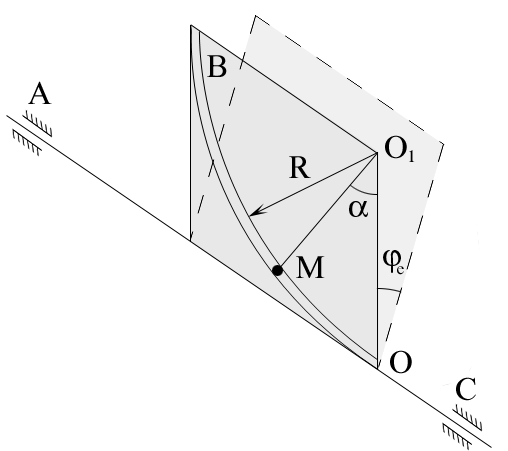
Пример 5.3. Пластина В вращается
вокруг неподвижной оси
,
согласно уравнению
(рис.
5.7).
На пластине по желобу движется точка, согласно уравнению
.
Вычислить абсолютную скорость и
абсолютное ускорение точки М в
момент времени t =
1с, если радиус желоба
.
Решение. Будем считать, что в момент
времени t = 1с угол
поворота
имеет такое значение, при котором тело
В располагается в плоскости
,
рис. 5.8.
Т
Рис. 5.8
Вычислим абсолютную скорость точки :
.
О
тносительная
скорость
.
Найдем положение точки М на пластине
В через 1с. Для этого вычислим
значение дуговой координаты
при
:
Если обозначить угол между радиусами
и
,
через тогда
.
Относительное движение точки задано
естественным способом. Приведем оси
к
точке М на траектории. Относительная
скорость
точки
М при
Вектор относительной скорости
лежит
в соприкасающейся плоскости
относительного движения – плоскость и направлена по касательной к траектории относительного движения – по оси (рис. 5.9, а).
Переносная скорость
.
В переносном движении точка движется
в соприкасающейся плоскости переносного
движения – плоскости
по окружности радиусом
(рис. 5.9, б).
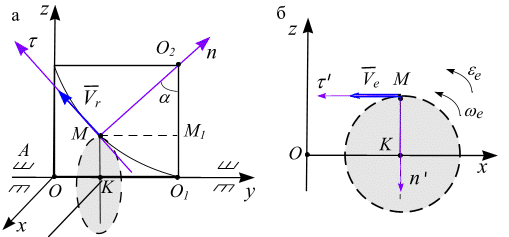
Рис.5.9
Задано уравнение вращения пластины В – , тогда
.
Переносное движение ускоренное, т.к.
>0,
>0,
дуговые стрелки
и
направлены в одну сторону (рис. 5.9, б).
Приведем оси
к
точке М в плоскости
.
Вычислим радиус кривизны траектории
при переносном движении точки М в
момент времени
(
):
=R
-
= R(1 - cos)
= 30(1 – cos(
))
= 30(1 – 0,707) = 8,79 см.
Переносная скорость Vе
.
Вектор переносной скорости
направлен
по касательной к траектории в точке М
– ось
(рис.
5.9, б). Направление оси
согласуется с направлением дуговой
стрелки
.
Так как в данном случае векторы
взаимно перпендикулярны, (вектор скорости
расположен в плоскости
,
вектор скорости
направлен по оси
,
т.е.
),
то модуль абсолютной скорости точки М
.
Вычислим абсолютное ускорение точки М. Абсолютное ускорение точки равно геометрической сумме относительного, переносного и Кориолисово ускорений
.
Относительное ускорение
.
Относительное движение точки задано
естественным способом – точка
движется
по окружности радиусом
в
соприкасающейся плоскости относительного
движения
.
Приведем к точке
оси
естественного трехгранника
(рис. 5.10, а). Ось
совпадает с направлением
,
ось
перпендикулярна
оси
и направлена вовнутрь вогнутости
траектории по радиусу
.
Рис. 5.10
Относительное ускорение равно
Здесь, при t = 1 с:
.
Точка
движется
с замедлением, поскольку векторы
>0,
<0,
вектор
и
вектор
имеют
разное направление по оси
.
Вектор
и вектор
направлены по осям
и
соответственно и лежат в плоскости
.
Переносное ускорение
.
Движение точки в ее переносном движении
– криволинейное. Точка движется по
окружности радиусом
в
соприкасающейся плоскости переносного
движения
.
Приведем к точке
оси
естественного трехгранника
(рис 5.8, б). Ось
совпадает с направлением
,
ось
перпендикулярно
оси
и направлена вовнутрь вогнутости, т.е.
по радиусу МК.
Переносное ускорение , рис. 5.10, б:
.
Здесь, при t = 1 с:
Вектор
и вектор
направлены по осям
и
соответственно.
Ускорение Кориолиса . Вектор ускорения Кориолиса
,
его модуль
.
Вектор направлен по оси вращения АС. Угол , угол между векторами и равен (рис. 5.11, а).
Итак,
Рис. 5.11
Направление вектора
по правилу Журавского: поворачиваем
на 90 по
направлению дуговой стрелке
вектор
направлен параллельно оси
(рис. 5.11, б).
Для вычисления модуля абсолютного
ускорения используем способ проекций.
Спроецируем все составляющие абсолютного
ускорения на оси
.
Имеем (рис. 5.10 и рис. 5.11, б):
Модуль абсолютного ускорения (рис. 5.12):
Рис. 5.12 |
Направление вектора
определим
геометрически. Совместим с точкой
декартову
систему координат
|
(рис.5.12).
Отложим проекции
абсолютного ускорения на оси координат
,
построим вектор
.
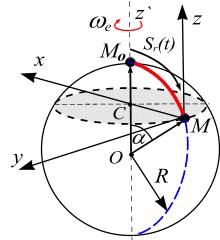
Пример 5.4. Шар радиусом R=1м
вращается вокруг вертикальной оси
по заданному уравнению
(рад). По меридиану шара движется точка
М по заданному уравнению
(м),
рис. 5.13. Дуга
отсчитывается от точки МО
меридиана. Вычислить абсолютную скорость
и абсолютное ускорение точки М в
момент времени t=1
с.
Решение. За переносное движение точки примем ее вращение вместе с шаром вокруг оси (рис. 5.13).
Рис. 5.13 |
Тогда относительным движением точки будет движение точки по меридиану шара. Определим положение точки М на меридиане в момент времени t=1с. Имеем:
Так как R=1 м, то положение точки определяется углом широты:
|
.
Совместим
декартову систему координат
с положением точки М
при
,
так, чтобы
было М
,
ось Мх
проходила через точку С
(рис. 5.13). В
переносном движении точка движется в
соприкасающейся плоскости
.
В относительном
движении точка движется
в соприкасающейся плоскости относительного
движения
.
Вычислим угловую скорость и угловое ускорения переносного движения:
;
.
Знак
(–) при
показывает, что вращение шара происходит
по часовой стрелке. Одинаковые знаки
при
и
,
показывают, что вращение шара в
рассматриваемый момент времени является
ускоренным.
Вычислим
модуль скорости переносного движения
(при t=1с)
–
.
Жестко скрепляем точку
с
шаром, точка будет двигаться по окружности
радиусом
в плоскости
(рис. 5.14, а). Тогда
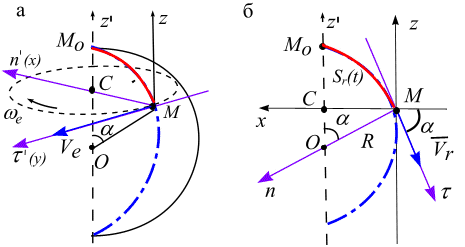
Рис. 5.14
Приведем
оси естественного трехгранника
к точке
в плоскости
.
Вектор скорости
переносного движения
будет
направлен по касательной
.
Оси
и
определяют соприкасающуюся
плоскость переносного движения и
совпадают с
осями
и
соответственно.
В относительном движении точка движется в соприкасающейся плоскости относительного движения (рис. 5.14, б). Приведем оси естественного трехгранника в плоскости . Скорость относительного движения точки – это скорость точки М при ее движении вдоль меридиана. Вычислим:
Знак
(+) при
указывает, что вектор
направлен в сторону возрастания дуговой
координаты
(рис. 5.14, б).
Вычислим абсолютную скорость точки
.
Модуль абсолютной скорости
.
Направление
вычислим
Рис. 5.15 геометрически, рис. 5.15.
Вычислим абсолютное ускорение точки
.
(а)
Точка
М
вращается вместе с шаром вокруг
неподвижной оси
в плоскости
.
Вычислим переносное ускорение
Модуль нормального ускорения
.
Ускорение
направлено по оси
(рис. 5.16, а).
Модуль касательной составляющей ускорения
.
Рис. 5.16
направлено по оси
и совпадает
с направлением вектора переносной
скорости
(рис.
5.16, а).
Вектор относительного ускорения расположен в плоскости (рис.5.16, б).
.
Модуль нормальной составляющей относительного ускорения
Ускорение
направлено по оси
,
т.е. к центру шара О
(рис. 5.16, б).
Модуль касательной составляющей относительного ускорения
.
Вектор
ускорения
направлен по оси
.
Так как
>0, то вектор
направлен в сторону возрастающих
значений
S
(рис. 5.16, б).
Вычислим ускорение Кориолиса
,
Направление
вектора
определим по правилу Жуковского (рис.
5.16, в). Вектор угловой скорости
направлен против оси вращения
(
<0).
Спроецируем на соприкасающуюся плоскость
переносного движения
вектор
и повернем полученную проекцию
вокруг
оси Мz
в плоскости
на
в сторону дуговой стрелки
(рис. 5.13, в). Ускорение Кориолиса
направлено по оси Му
и совпадает с направлением ускорения
.
Для вычисления модуля абсолютного ускорения используем способ проекций. Спроецируем все составляющие абсолютного ускорения на оси .
Имеем (рис. 5.16, а, б, в):
;
;
.
Модуль абсолютного ускорения
.
Направление вектора вычислим по направляющим косинусам.
,
;
,
;
,
.
Ответ.
;
.