124

§ 5. Сложное движение точки

Содержание. Основные понятия – абсолютное, относительное и переносное движения. Теорема о сложении скоростей. Сложение скоростей точки в общем случае переносного движения. Сложение ускорений точки в общем случае переносного движения. Ускорение Кориолиса. Правило Жуковского. Примеры.

§ 5.1 Основные понятия

Рис.5.1

Пусть точка движется по плоскому телу (S). Свяжем с телом систему координат Охуz. Пусть само тело (S) движется относительно некоторой системы координат , которую по отношению к наблюдателю будем считать неподвижной (рис. 5.1). Тогда система отсчета Охуz будет двигаться относительно неподвижной системы .

Рассмотрим движение точки по отношению к двум системам координат – подвижной и неподвижной. Движение точки М относительно подвижной системы отсчета Охуz называется относительным. Относительное движение точки может быть прямолинейным или криволинейным. Характеристики этого движения – траектория, скорость, ускорение называются относительными. Их отмечают индексом r: для относительной скорости – и для относительного для ускорения – .

Движение точки М относительно неподвижной системы отсчета О₁х₁у₁z₁ называется абсолютным или сложным. Траектория, скорость и ускорение точки, относительно неподвижной системы координат называются абсолютными. Скорость и ускорение абсолютного движения отмечают буквами и без индексов.

Переносным движением точки М называют движение, которое она совершает вместе с подвижной системой отсчета как точка, жестко скрепленная с телом (S) в рассматриваемый момент времени. Вследствие относительного движения движущаяся точка М в различные моменты времени совпадает с различными точками тела (S). Переносная скорость и переносное ускорение точки совпадают со скоростью и ускорением той точки тела (S), в которой в заданный момент времени находится движущаяся точка М. Переносное движение отмечают индексом е: для скорости – , для ускорения – .

§ 5.2. Абсолютная скорость точки

Пусть заданы уравнения относительного движения точки , т.е. заданы уравнения движения точки относительно системы координат Охуz, а также заданы уравнения движения полюса тела (S) и задано вращение тела вокруг оси .

Теорема. Абсолютная скорость точки равна геометрической сумме ее относительной и переносной скоростей:

Рис. 5.2

. (5.1)

Доказательство. Пусть точка М движется по телу (S) относительно подвижной системы координат . Предположим, что центр подвижной системы координат О движется криволинейно относительно неподвижной системы отсчета О₁х₁у₁z₁, а оси координат Охуz вращаются вместе с телом (S) вокруг оси с угловой скоростью (рис. 5.2).

Абсолютное движение точки , т.е. движение точки относительно неподвижной системы координат О₁х₁у₁z₁, зададим радиус–вектором , а относительное движения точки М, т.е. движение точки относительно подвижной системы координат определим радиус – вектором . Тогда

, (5.2)

здесь:

– , – координаты точки М относительно неподвижной системы координат О₁х₁у₁z₁; единичные орты неподвижной системы координат;

– , – координаты полюса О относительно неподвижной системы координат О₁х₁у₁z₁;

– , x, y, z – координаты точки М относительно подвижной системы координат Оxyz, – единичные орты подвижной системы координат.

Абсолютная скорость по определению равна . Продифференцируем по времени векторное равенство (5.2):

.

Вычислим :

, (5.3)

здесь: – проекции вектора скорости полюса О – на оси неподвижной системы координат.

Вычислим (отметим, что единичные орты подвижной системы координат – функции времени):

(5.4)

Здесь проекции скорости точки М относительно подвижной системы координат, т.е. проекции относительной скорости точки М .

Производные по времени единичных векторов вычислим по формуле Эйлера ( ):

(5.5)

Перепишем (5.4) с учетом (5.5)

(5.5’)

итак,

. (5.6)

Таким образом, складывая (5.3) и (5.6), получим

(5.7)

Первое и третье слагаемы в (5.7) определяют движение подвижной системы координат, т.е. определяют скорость переносного движения точки М – . Следовательно, выражение (5.7) будет иметь структуру формулы (5.1), т.е.

.

Здесь: скорость относительного движения.

Скорость переносного движения выражается формулой

(5.8)

Рассмотрим частные случаи вычисления переносной скорости.

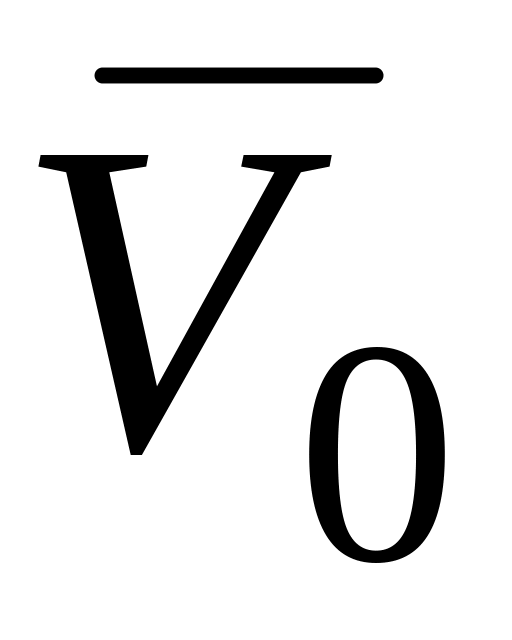1. Подвижная система координат вместе с телом движется поступательно со скоростью . В этом случае =0 и, следовательно, согласно (5.8)

.

Переносная скорость совпадает со скоростью тела .Тогда абсолютна скорость

2. Подвижная система координат вместе с телом вращается вокруг неподвижной оси c угловой скоростью . В этом случае 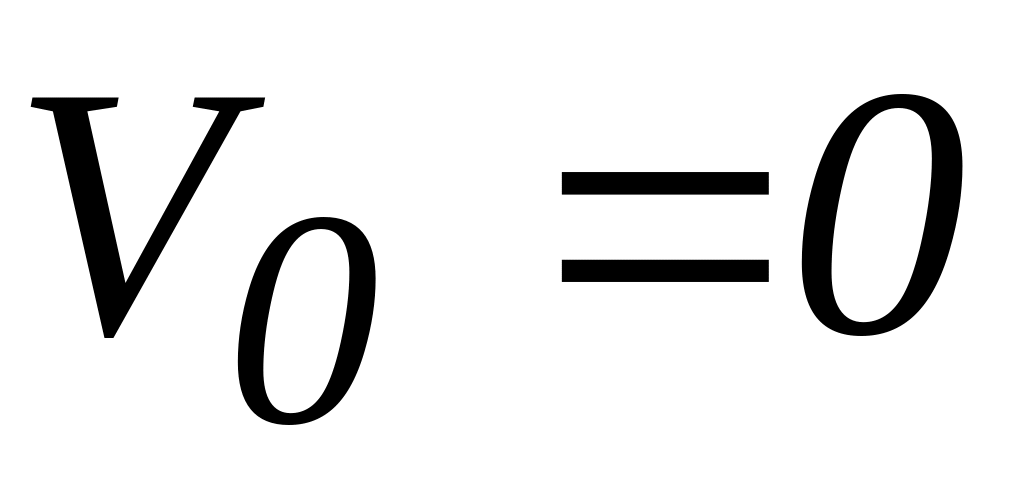, тогда переносная скорость, согласно (5.8)

Переносная скорость не совпадает со скоростью тела .Тогда абсолютна скорость

П

Рис. 5.3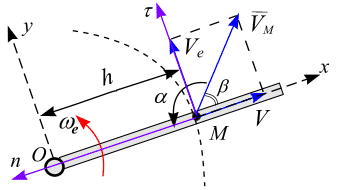

ример 5.1. Стержень вращается в плоскости вокруг неподвижного центра с угловой скоростью . Точка М скользит вдоль стержня со скоростью . Вычислить абсолютную скорость точки (рис. 5.3).

Решение. Точка участвует в двух движениях: движется вдоль стержня и, кроме того, вращается вместе со стержнем. Свяжем подвижную систему координат с центром (рис. 5.3). Движение точки вдоль стержня (по оси ) будет относительным т.е. .За время точка пройдет по оси путь , равный

Для вычисления переносной скорости , жестко скрепим точку со стержнем на расстоянии от центра вращения . Приведем оси естественного трехгранника к точку . Тогда в переносном движении точка будет двигаться по окружности радиусом со скоростью, равной

.

Вектор и направлен по оси .

Так как векторы и ортогональны, абсолютная скорость точки будет равна

.

Вычислим угол между и осью :

, , .

Пусть , , .

Тогда ;

, .

, , .

Ответ. Абсолютная скорость точки равна

, .