§4.6. Примеры решения задач

Пример 1. Для спуска груза 4 диск 1 вращается вокруг неподвижной оси, согласно уравнению: и приводит во вращение диски 2 и 3, которые имеют общую неподвижную ось вращения и жестко скрепленные друг с другом (рис. 4.13). Диск 1 и 2 связаны зубчатой передачей, r₁=0,2м, R₂=0,4м, r₃=0,3м. Груз 4 и диск 1 связаны нерастяжимым тросом.

Рис. 4.13

Вычислить в момент времени t=5с:

1. скорость и ускорение груза 4;

2. ускорение в точке А второго диска.

Решение. Вычислим угловую скорость и угловое ускорение ведущего диска 1.

Имеем

(а)

В этот момент времени первый диск вращается по часовой стрелке ускоренно т. к. <0 и <0, дуговые стрелки ₁ и ₁ следует направить в одну сторону (рис. 4.14, а). Тогда диски 2 и 3 за счет зубчатой передачи будут вращаться против часовой стрелки.

Запишем уравнения связи. Для этого, согласно (4.8), свяжем перемещение точек соприкосновения 1-го и 2-го дисков, 3-его диска и тела 4 (через нерастяжимый трос). Имеем:

;

.

а	б
Рис. 4.14

Вычислим угловые скорости и угловые ускорения дисков:

(б)

Вычислим ускорение в точке А диска 2 . Свяжем с точкой А оси естественного трехгранника , рис. 4.14, б. Имеем:

; ;

.

Вычислим угол между вектором и :

, .

Направление вектора показано на рис. 4.14, б.

Р ис.4.15

Пример 2. Механизм (рис. 4.15) состоит из двух ступенчатых дисков (2 и 3), связанных ременной передачей, барабана 4, соединенного с диском 3 нерастяжимым тросом, и груза 1, привязанного к концу нерастяжимой нити, намотанной на малый радиус диска 2.

Уравнение движения ступенчатого диска 3 задано уравнением: (рад). Радиусы ступеней дисков составляют соответственно м, м; м; м; радиус барабана м.

В момент времени с вычислить:

Решение. Вычислим угловую скорость и угловое ускорение ведущего диска 3 для заданного момента времени с и определим направление движения звеньев механизма:

(с^-1);

(с^-2).

Движение ведущего диска 3 ускоренно и направлено против часовой стрелки, т.к. , . Следовательно, движение всех звеньев механизма будет ускоренным, как показано дуговыми стрелками на рис. 4.16.

1. Запишем уравнения связей для заданного механизма.

Ведущим звеном системы является ступенчатый диск 3.

Уравнение связи между дисками 3 и 2:

, ,

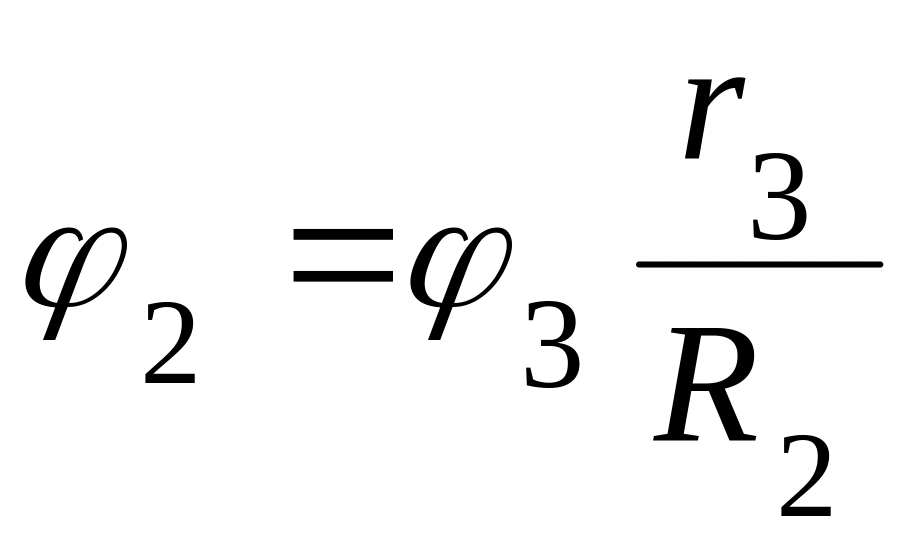тогда 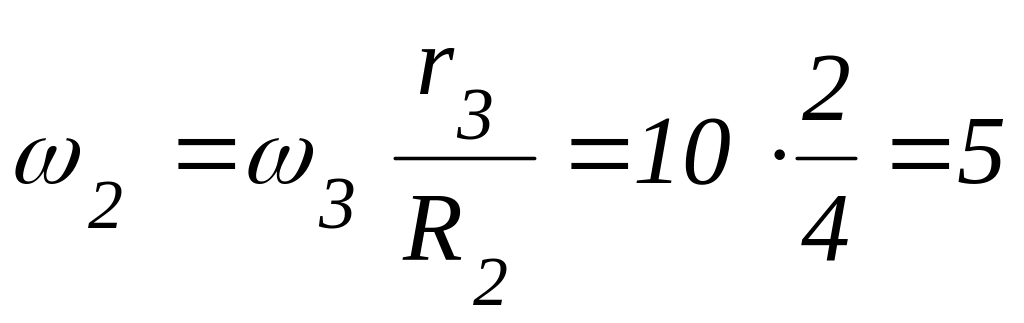(с^-1), 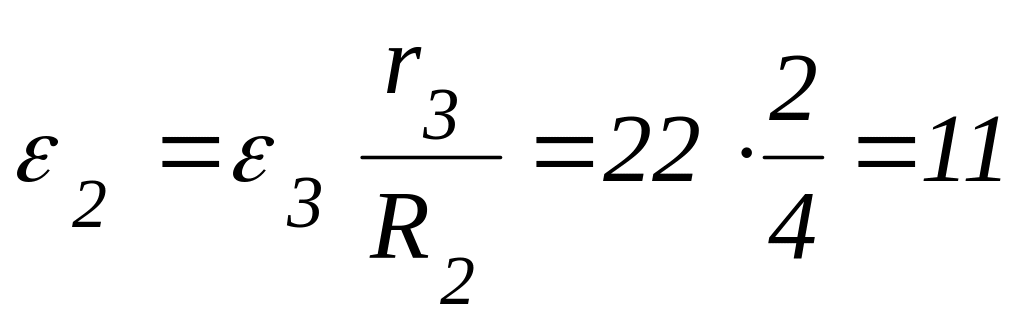(с^-2).

Рис. 4.16

Уравнение связи между 3-им диском и барабаном 4:

, ,

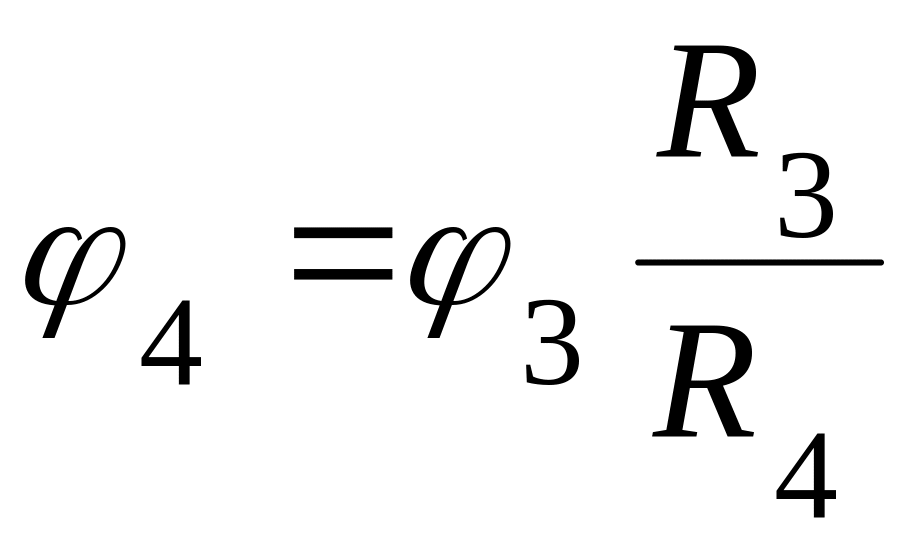тогда (с^-1) (с^-2).

Уравнение связи между 3-им диском и грузом 1:

,

тогда (м/с) (м/с²).

Вычислим скорости точек.

2. Точки С и D находятся на ободе диска 3. Привязываем оси естественного трехгранника 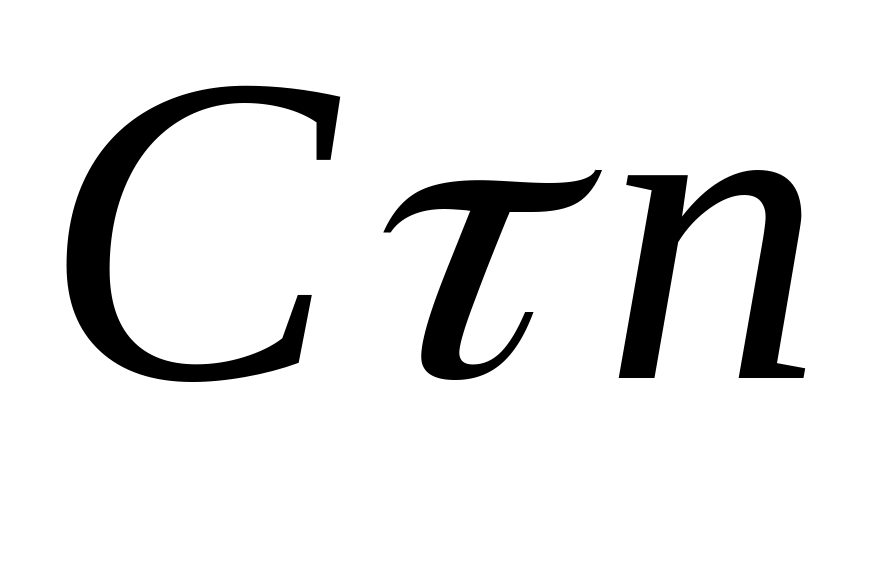и 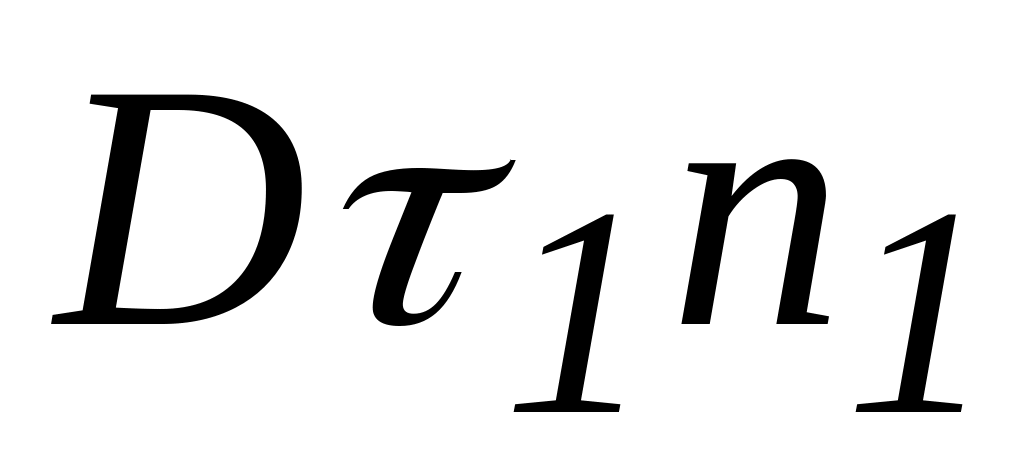к точкам C и D соответственно (рис. 4.20). Имеем:

(м/с); (м/с).

Векторы скоростей точек расположены на осях и соответственно.

Рис. 4.17

Точки А и В находятся на ободе диска 2. Привязываем оси естественного трехгранника к точка А и В и соответственно (рис. 4.17). Имеем:

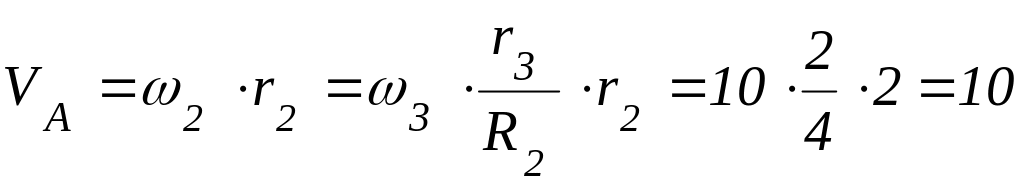(м/с);

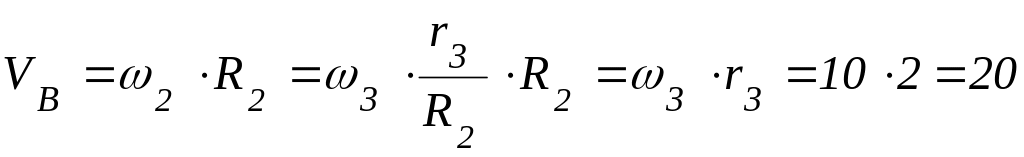(м/с).

Векторы скоростей точек расположены на осях и соответственно.

Точка Е находится на ободе барабана 4. Привязываем оси естественного трехгранника к точкам Е (рис. 4.17). Имеем:

(м/с).

Вектор скорости расположен на оси .

Скорость груза 1:

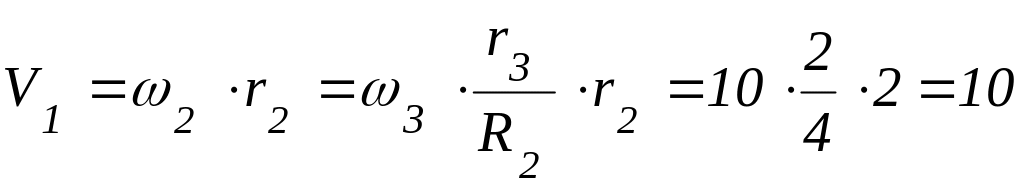(м/с).

3. Вычислим ускорения точек С, Е.

Точка С находится на ободе диска 3, следовательно, рис. 4.17:

, где (м/с²),

(м/с²);

(м/с²).

В екторы нормального и касательного ускорений точки С расположены на осях и (точка С) соответственно.

Точка Е находится на ободе барабана 4 (рис. 4.18). Вычисляем ускорение точки Е:

.

Здесь

Рис. 4.18

(м/с²);

(м/с²).

Векторы нормального и касательного ускорений точки Е расположены на осях и (точка С) соответственно.

Вычислим ускорение груза 1.

(м/с²).

Ответ: (м/с), (м/с), (м/с), (м/с),

(м/с), (м/с²), (м/с²), (м/с²).

1 Для самостоятельного изучения.