
§ 4.4. Преобразование простейших движений
Преобразование поступательного движения тела во вращательное. Рассмотрим диск, на обод которого намотана нерастяжимая нить (нерастяжимый трос, канат и.т.д.) за конец которой прикреплен груз (рис. 4.10).
Запишем уравнение,
связывающее угловую (![]() )
и дуговую (
)
и дуговую (![]() )
координаты, иначе говоря – уравнение
связи. Для этого свяжем перемещение
точек нити и точек, лежащих на ободе
диска, радиус которого равен
.
Пусть тело опустилось на
,
тогда диск повернется на угол
)
координаты, иначе говоря – уравнение
связи. Для этого свяжем перемещение
точек нити и точек, лежащих на ободе
диска, радиус которого равен
.
Пусть тело опустилось на
,
тогда диск повернется на угол
![]() против часовой стрелки
против часовой стрелки
Р |
. Известно, что
длина дуги, радиус окружности и угол
Тогда:
|
Здесь , .
Преобразование вращательного движения вокруг одной неподвижной оси во вращательное движение вокруг другой неподвижной оси. Преобразование вращения одного твердого тела вокруг неподвижной оси во вращение второго твердого тела вокруг другой неподвижной оси осуществляется посредством зубчатого или фрикционного (за счет сил трения) зацепления двух дисков (рис. 4.11, а, б), или при помощи ременной передачи (рис. 4.11, в, г).
При внешнем зацеплении (рис. 4.11, а) и прямой ременной передаче (рис. 4.11, в) направления вращений обоих дисков совпадают; при внутреннем зацеплении (рис. 4.11, б) и скрещивающейся ременной передаче (рис. 4.11 г) направление вращения дисков противоположно.
Примем за ведущее
звено диск 1, за ведомое– диск 2. Пусть
диск 1 за время
![]() повернулся
по часовой стрелке на угол
повернулся
по часовой стрелке на угол
![]() ,
тогда диск 2 повернется против часовой
стрелки на угол
,
тогда диск 2 повернется против часовой
стрелки на угол
![]() .
Тогда путь
,
пройденный точками на ободе дисков,
находящихся в зацеплении, или связанные
ременной передачей, одинаков. На этом
основании запишем уравнение связи.
Напомним, что длина дуги, угол поворота
и радиус связаны соотношением:
.
Тогда путь
,
пройденный точками на ободе дисков,
находящихся в зацеплении, или связанные
ременной передачей, одинаков. На этом
основании запишем уравнение связи.
Напомним, что длина дуги, угол поворота
и радиус связаны соотношением:
![]() .
Тогда, для всех типов зацепления имеем
.
Тогда, для всех типов зацепления имеем
![]() . (4.8)
. (4.8)
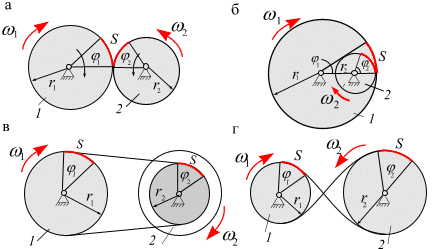
Рис. 4.11
Дифференцируя по времени правые и левые части (а), получим
 .
.
Здесь – угловая скорость тела, – угловое ускорение тела,
r1, r2 – радиусы дисков.
Угловые скорости дисков обратно пропорциональны числам зубцов (zi), или радиусам (ri), или диаметрам (di) дисков.
![]() .
.
здесь d1, d2 – диаметры дисков; z1, z2 – число зубцов каждого диска.
Часто применяется соединение дисков, когда два диска вращаются вокруг одной неподвижной оси. Если при этом они жестко соединены друг с другом, то их угловые скорости равны (на рис. 3.25, в – второй диск).
§ 4.5. Формулы Эйлера
В
Рис. 4.12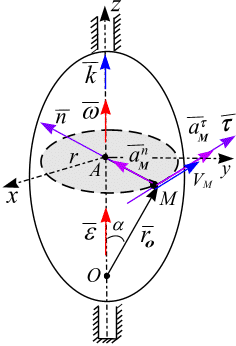
Скорость точки М по модулю и направлению можно представить векторным произведением
![]() ,
(4.9)
,
(4.9)
где
![]() - радиус-вектор точки М,
проведенный из произвольной точки оси
вращения
- радиус-вектор точки М,
проведенный из произвольной точки оси
вращения
![]() ,
например точки О.
Записанное выражение (4.9) называется
векторной
формулой Эйлера.
Убедимся в справедливости этой формулы.
Вектор
,
например точки О.
Записанное выражение (4.9) называется
векторной
формулой Эйлера.
Убедимся в справедливости этой формулы.
Вектор
![]() перпендикулярен плоскости
,
т.е. лежит в плоскости вектора скорости
перпендикулярен плоскости
,
т.е. лежит в плоскости вектора скорости
![]() ,
рис. 4.12. Модуль векторного произведения
,
рис. 4.12. Модуль векторного произведения
![]() ,
,
так как
![]() .
Таким образом, векторное произведение
.
Таким образом, векторное произведение
![]() по модулю и направлению определяет
скорость точки М.
по модулю и направлению определяет
скорость точки М.
Вычислим вектор ускорения:
![]()
![]() .
.
Учитывая, что
![]() ,
,
![]() ,
получаем
,
получаем
![]() .
(4.10)
.
(4.10)
Здесь для первого слагаемого
![]() .
.
Вектор
![]() перпендикулярен плоскости
,
т.е. лежит в плоскости вектора скорости
перпендикулярен плоскости
,
т.е. лежит в плоскости вектора скорости
![]() .
(рис. 4.12). Итак,
.
(рис. 4.12). Итак,
![]() .
.
Для второго слагаемого (4.9) имеем
![]()
здесь векторы
![]() и
взаимно перпендикулярны. Направление
вектора
и
взаимно перпендикулярны. Направление
вектора
![]() перпендикулярно плоскости
,
т.е. лежит в плоскости вектора скорости
перпендикулярно плоскости
,
т.е. лежит в плоскости вектора скорости
![]() .
Итак,
.
Итак,
![]() .
.
Первое слагаемое
соответствует касательному ускорению
![]() ,
а второе –нормальному
,
а второе –нормальному
![]() ,
т.е.
,
т.е.
![]() . (4.11)
. (4.11)
Справедливость формул подтверждена.
Формулы Эйлера
|

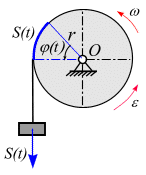 ис.
4.10
ис.
4.10