- •§ 3. Естественный способ задания движения точки
- •§ 3.1. Определения
- •§ 3.2. Оси естественного трехгранника
- •§ 3.3. Скорость точки при естественном способе задания движения
- •§ 3.4. Ускорение точки при естественном способе задания движения
- •§ 3.5. Связь координатного и естественного способов
- •§ 3.6. Частные случаи криволинейного движения точки
§ 3.6. Частные случаи криволинейного движения точки
Криволинейное
движение точки. При
криволинейном движении точки вектор
нормального ускорения
![]() всегда направлена внутрь
вогнутости траектории вдоль оси
всегда направлена внутрь
вогнутости траектории вдоль оси
![]() .
Вектор касательного ускорения
.
Вектор касательного ускорения
![]() при
при
![]() направлен по направлению оси
,
а при
направлен по направлению оси
,
а при
![]() –противоположно направлению оси
(рис. 3.14).
–противоположно направлению оси
(рис. 3.14).

Рис. 3.14
Касательное
ускорение
![]() ,
когда (рис. 3.15, а).
,
когда (рис. 3.15, а).
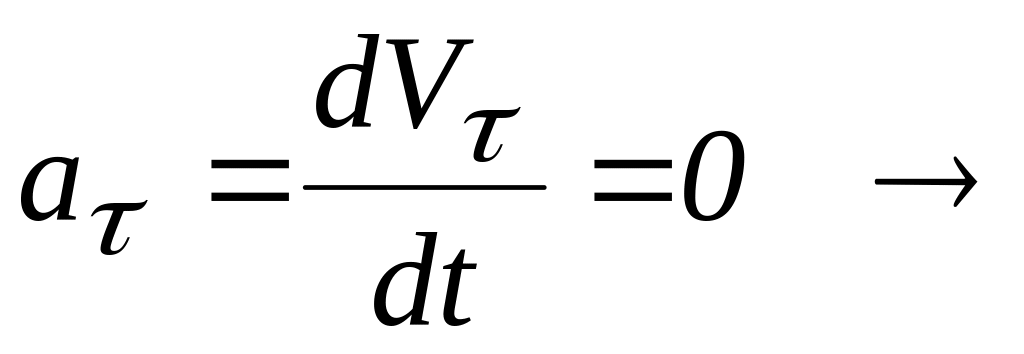
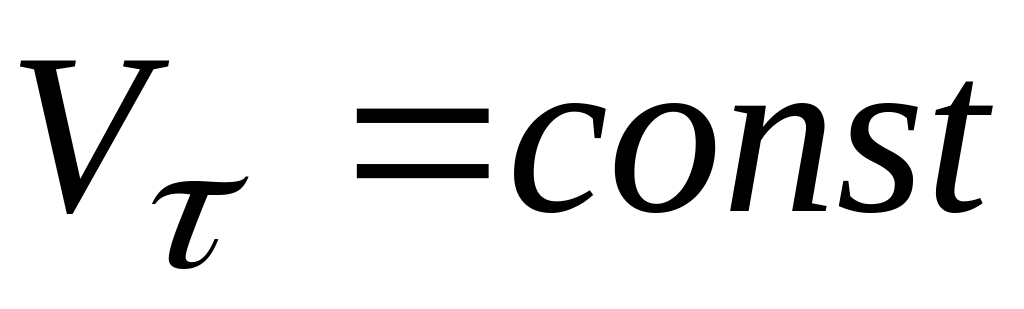 ,
т.е. при равномерном движении точки;
,
т.е. при равномерном движении точки;
2. В моменты времени,
когда
![]() ,
,
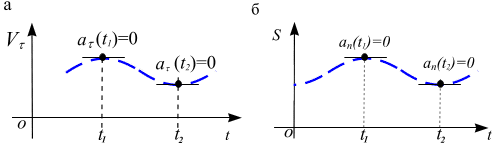
Рис. 3.15
Нормальное ускорение
![]() ,
когда
,
когда
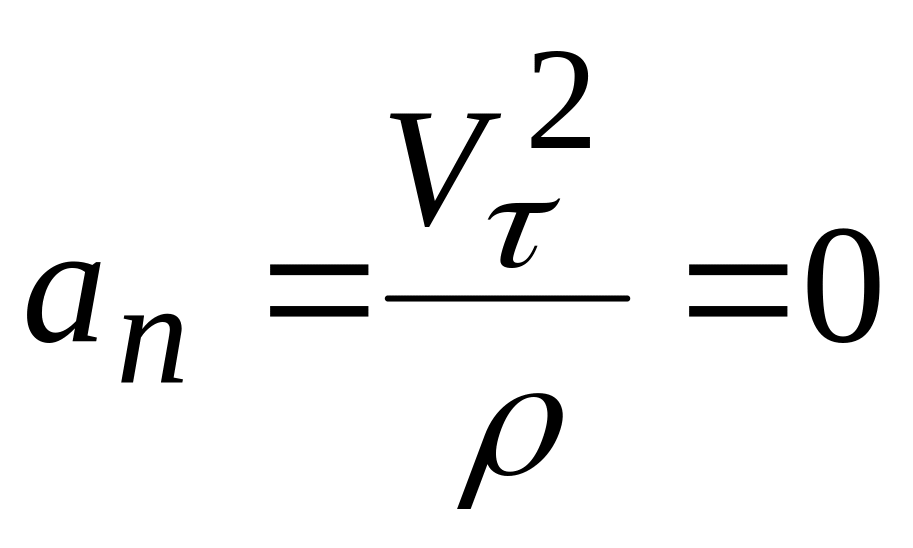 ,
это условие выполняется при
,
это условие выполняется при
 ,
т.е. при прямолинейном движении точки.
,
т.е. при прямолинейном движении точки.Когда
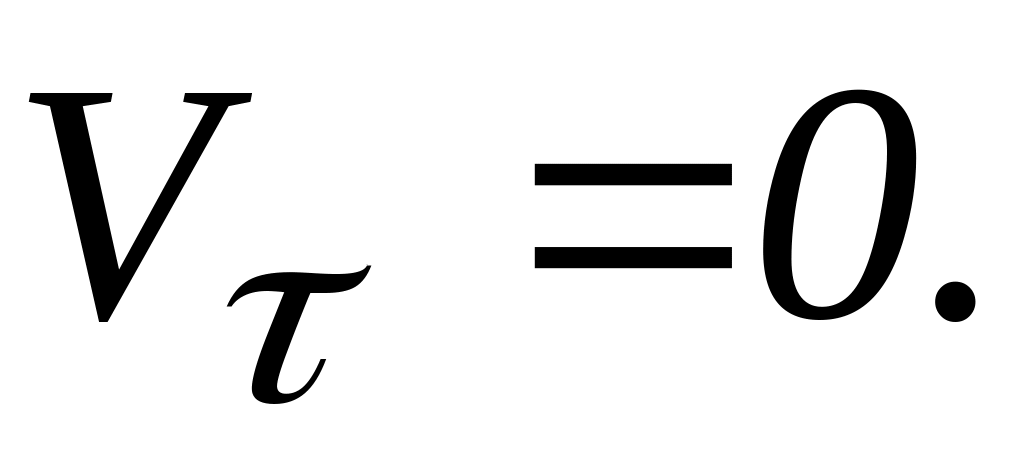
В точках перегиба, когда происходит изменение выпуклости траектории на вогнутость и наоборот (рис. 3.15, б).
Круговое движение
точки. Введем
радиус-вектором
![]() .
Совместим начало радиус-вектора с
центром окружности О,
полярную ось
.
Совместим начало радиус-вектора с
центром окружности О,
полярную ось
![]() направим по радиусу, рис. 3.16, а. Тогда,
при движении точки будет меняться только
угол между радиус-вектором и осью
направим по радиусу, рис. 3.16, а. Тогда,
при движении точки будет меняться только
угол между радиус-вектором и осью
![]() (рис.3.16, а), модуль радиус-вектора остается
постоянным. Следовательно, описывать
движение точки можно одним параметром
– углом
(рис.3.16, а), модуль радиус-вектора остается
постоянным. Следовательно, описывать
движение точки можно одним параметром
– углом
![]() .
Зададим движение точки естественным
способом. Введем оси естественного
трехгранника
.
Зададим движение точки естественным
способом. Введем оси естественного
трехгранника
![]() и привяжем их к движущейся точки
.
Нормальная ось
и привяжем их к движущейся точки
.
Нормальная ось
![]() совпадает с направлением радиуса
окружности и проходит через центр
окружности, касательная ось
совпадает с направлением радиуса
окружности и проходит через центр
окружности, касательная ось
![]() направлена в сторону движения точки и
перпендикулярна радиусу (рис.3.16, б).
направлена в сторону движения точки и
перпендикулярна радиусу (рис.3.16, б).
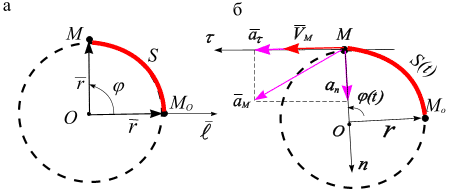
Рис. 3.16
Пусть точка движется
по окружности радиуса
![]() против часовой стрелки (рис. 3.16 б). При
,
точка занимала положение
против часовой стрелки (рис. 3.16 б). При
,
точка занимала положение
![]() ,
за время
точка
прошла путь S
и заняла положение
,
а радиус-вектор
,
за время
точка
прошла путь S
и заняла положение
,
а радиус-вектор
![]() повернулся вслед за точкой на угол
повернулся вслед за точкой на угол
![]() .
.
Зададим движение точки естественным способом. Введем оси естественного трехгранника, оси и . Соприкасающаяся плоскость совпадает с плоскостью движения точки, ось совпадает с радиусом и проходит через центр окружности, ось направлена в сторону движения точки и перпендикулярна радиусу.
|
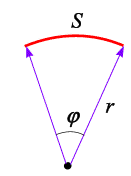
Известно, что длина дуги, радиус окружности и угол связаны между собой (рис. 3.17):
Введем обозначения:
|
Рис. 3.17 |
Вычислим скорость и ускорение точки:
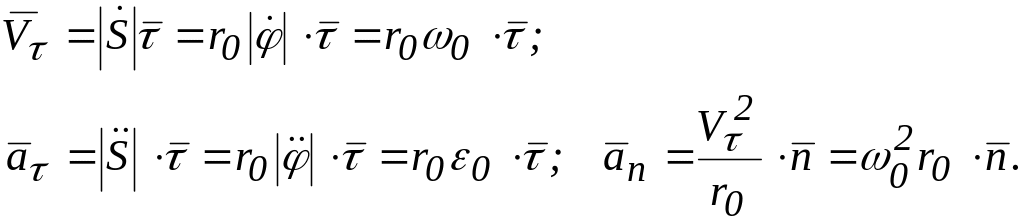 (3.17)
(3.17)
Знак производной
![]() определяет направление движения точки:
определяет направление движения точки:
при
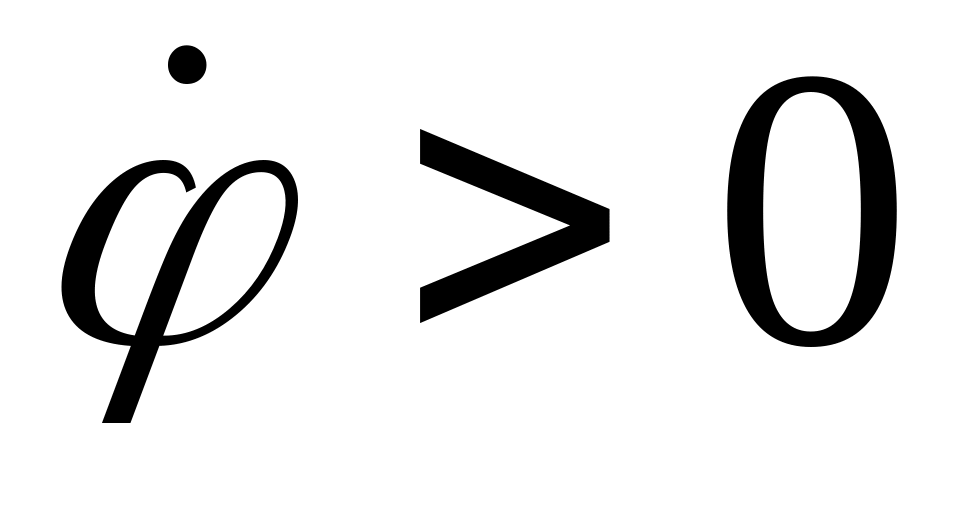 ,
точка движется против часовой стрелки,
,
точка движется против часовой стрелки,
при
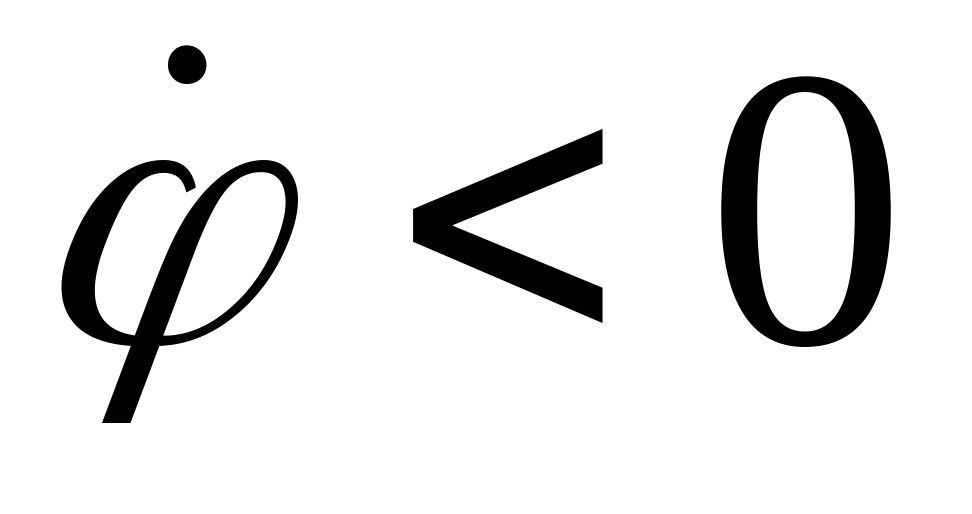 ,
точка движется по часовой стрелки;
,
точка движется по часовой стрелки;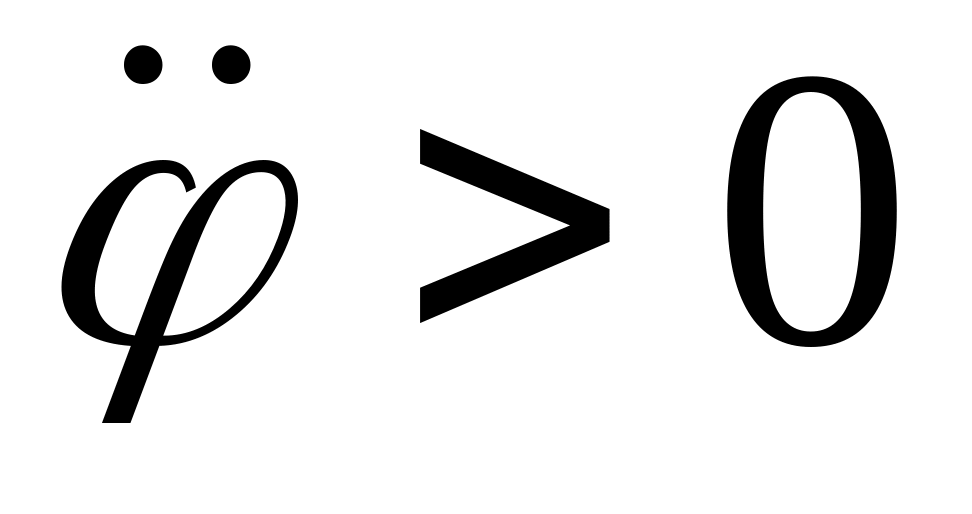 ,
,
или
,
,
или
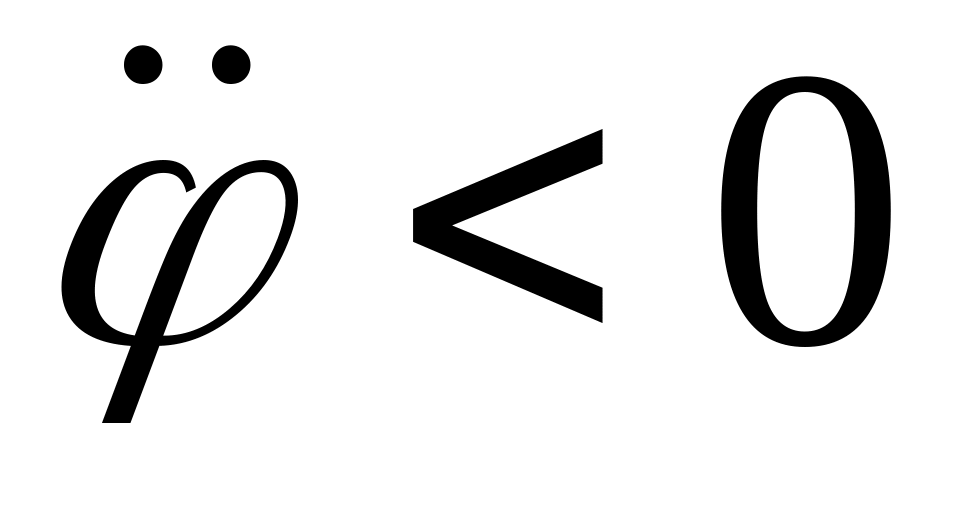 ,
–
точка движется ускоренно;
,
–
точка движется ускоренно;, или
 ,
,
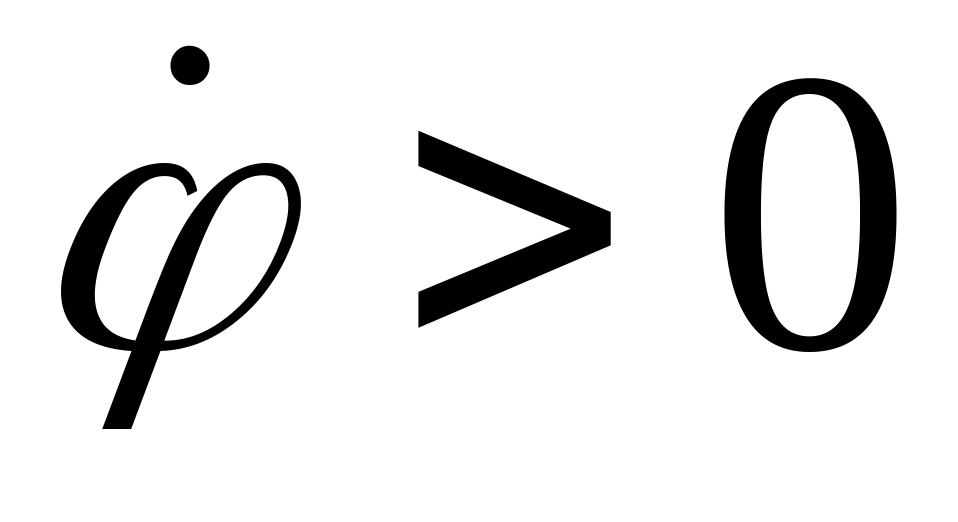 –
точка движется замедленно.
–
точка движется замедленно.
Круговое движение точки
|
Угол
![]() ,
угол между ускорением точки
,
угол между ускорением точки
![]() и нормальной осью
вычислим из равенства, рис. 3,16, б:
и нормальной осью
вычислим из равенства, рис. 3,16, б:
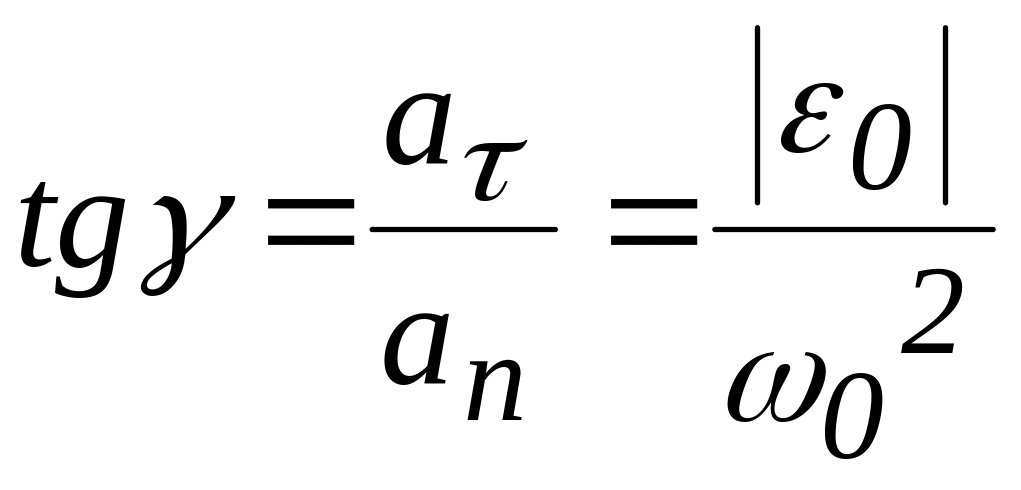 .
.
При равномерном
круговом движении
![]() ,
тогда угол между ускорением
и нормальной осью
,
тогда угол между ускорением
и нормальной осью
![]() равен
нулю, т.е. вектор ускорения направлен
по радиусу к центру окружности.
равен
нулю, т.е. вектор ускорения направлен
по радиусу к центру окружности.
1
Производная функции
![]() равна пределу отношения приращения
функции
равна пределу отношения приращения
функции
![]() к приращению аргумента
к приращению аргумента
![]() ,
когда
,
когда
![]() :
:
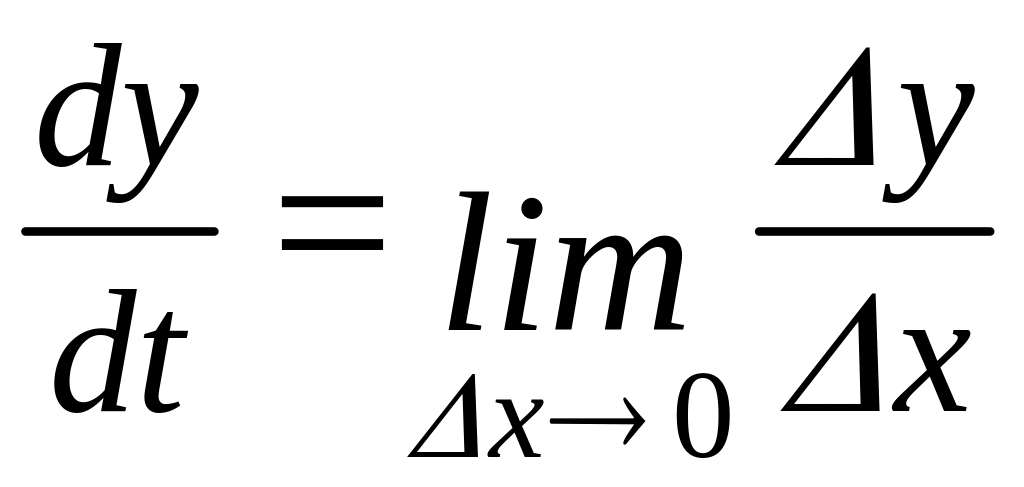 .
.