§ 3.3. Скорость точки при естественном способе задания движения

Пусть движение точки задано естественным способом. Вычислим скорость точки. Положение точки М на кривой можно описать радиус – вектором , начало которого находится в центре О (рис. 3.7). Траектория определяет радиус-вектора, т.е радиус-вектор в данном случае является сложной функцией от времени, т.е. .

Вычислим скорость точки М, имеем:

(3.5)

Направление приращения радиус-вектора в пределе совпадает с касательной осью в точке М (рис.3.7). Согласно определению производной

где – приращение дуговой координаты. Вектор направлен в сторону возрастания дуговой координаты и совпадает с касательной к траектории в точке . Покажем, что этот вектор является единичным. Из рис. 3.7 видно, что

Скорость

(3.6)

Величина называется алгебраической скоростью точки. Знак производной определяет направление вектора скорости по .

§ 3.4. Ускорение точки при естественном способе задания движения

В соответствии с определением ускорения, имеем

. (3.7)

Вектор ускорения имеет два слагаемых. Первое слагаемое в выражении (3.7)– вектор , направлен по и определяет изменение модуля скорости. Второе слагаемое – вектор имеет направление вектора .

Покажем, что во втором слагаемом вектор перпендикулярен вектору . Имеем: скалярный квадрат вектора равен единице:

. (а)

поэтому векторы и перпендикулярны друг другу (рис. 3.8).

Справка Скалярный квадрат , если , то . Скалярное произведение когда

Дифференцируя по времени обе части тождества (а) получим:

.

поэтому векторы и перпендикулярны друг другу (рис. 3.8).

Направим единичный вектор по вектору , тогда

. (3.8)

По определению производной¹, имеем

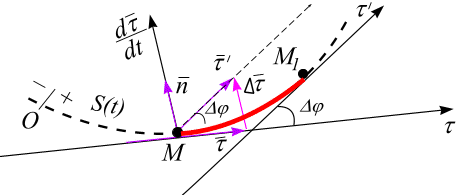
Рис. 3.7

. (3.9)

Вектор , как результат вычитания двух единичных векторов ( ), направлен на встречу вектора , т.е. направлен вовнутрь вогнутости траектории. Вычислим величину (рис. 3.8). Поскольку <<1, имеем

Подставляя полученный результат в (3.9) имеем

. (3.10)

При криволинейном движении точки угол смежности зависит от , т.е.  = (S(t)).

Используя (3.8) и (3.10) и дифференцируя по времени  (S (t)) как сложную функцию, получим

. (3.11)

Здесь, – радиус кривизны.

Вектор и совпадающий с ним по направлению единичный вектор направлены параллельно предельному положению вектора при , т.е. векторы и расположены в соприкасающейся плоскости

	кривой. Единичный вектор перпендикулярен вектору , направлен по главной нормали кривой в сторону ее вогнутости, так как в эту сторону направлено предельное положение вектора (рис.3.8). Итак, ускорение точки при естественном способе задания движения (3.7) запишем в виде или (3.12)
Рис. 3.9

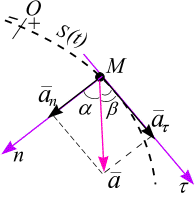
Вектор ускорения точки М раскладывается на две векторные проекции по осям естественного трехгранника (рис.3.10). Проекция ускорения на ось называется касательным ускорением и обозначается :

. (3.13)

Проекция ускорения на ось называется нормальным ускорением и обозначается :

(3.14)

Таким образом,

. (3.15)

Учитывая ортогональность и , имеем (рис. 3.19):

. (3.16)

Касательное ускорение характеризует изменение величины скорости, нормальное – изменение направления вектора скорости.

Естественный способ задания движения – + траектория , – касательное ускорение; - нормальное ускорение;.