
- •§ 3. Естественный способ задания движения точки
- •§ 3.1. Определения
- •§ 3.2. Оси естественного трехгранника
- •§ 3.3. Скорость точки при естественном способе задания движения
- •§ 3.4. Ускорение точки при естественном способе задания движения
- •§ 3.5. Связь координатного и естественного способов
- •§ 3.6. Частные случаи криволинейного движения точки
§ 3. Естественный способ задания движения точки
Содержание: естественный способ задания движения точки. Определения. Оси естественного трехгранника. Скорость и ускорение точки в проекциях на оси естественного трехгранника, касательное и нормальное ускорение точки.
§ 3.1. Определения
П
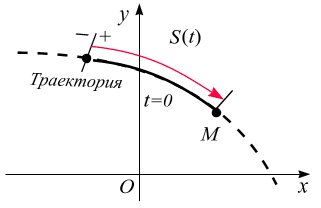 Рис.
3.1
Рис.
3.1
– траектория движения точки;
– начало и направление увеличения дуговой координаты;
– уравнение
движения точки по траектории, как функция
времени:
![]() где S
– дуговая координата, отчитываемая от
начала движения.
где S
– дуговая координата, отчитываемая от
начала движения.
Для задания
уравнения движения точки по траектории
необходимо выбрать на заданной траектории
точку О,
принимаемую за начало отсчета дуговой
координаты (рис. 3.1). Будем называть
положительным то направление, которое
соответствует возрастанию дуговой
координаты. Обычно за
![]() принимают момент времени, в который
движущая точка проходит через выбранную
точку О.
принимают момент времени, в который
движущая точка проходит через выбранную
точку О.
Движение точки может быть задано различными способами, например таблицей значений, графиком, одной или несколькими функциями.
Примером естественного способа задания движения является движение поезда: траектория и направление движения определены рельсами, а уравнение движения задано таблицей – расписанием движения поезда.
Рассмотрим движение точки, уравнение движения которой можно задать аналитически. Пусть шар падает вертикально вниз. В табл. 3.1 даны значения: время в секундах, расстояния в метрах. За нулевой момент времени выбираем момент начала падения шара. Через 1с после начала падения шар пролетает 5м, через 2 с – 20 м, через 3 с – 45 м (табл. 3.1).
Табл. 3.1
Расписание движения падающего шара
|
|
1 |
2 |
3 |
4 |
5 |
6 |
S, м |
0 |
5 |
20 |
45 |
80 |
125 |
180 |
Н
Рис. 3.2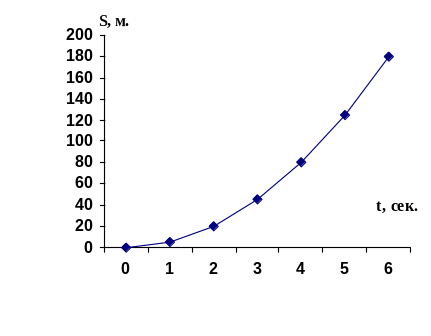
![]() ,
S(3)=
S(3)=
,
S(3)=
S(3)=![]() ,
и.т.д. Если отложить эти числа на графике
в системе координат (
,
и.т.д. Если отложить эти числа на графике
в системе координат (![]() )
(рис. 3.2), то получим график зависимости
пути, пройденному шаром от времени
падения – графиком является парабола,
которая описывается формулой
)
(рис. 3.2), то получим график зависимости
пути, пройденному шаром от времени
падения – графиком является парабола,
которая описывается формулой
![]()
Сравним два вида
задания движения – координатный и
естественный. Если движение точки задано
координатным способом:
![]() ,
то для перехода к естественному способу
задания необходимо:
,
то для перехода к естественному способу
задания необходимо:
Составить и построить уравнение траектории –
 ;
;Отметить положение точки в начальный момент времени и направление движения;
Составить уравнение движения точки по траектории, как функция времени:
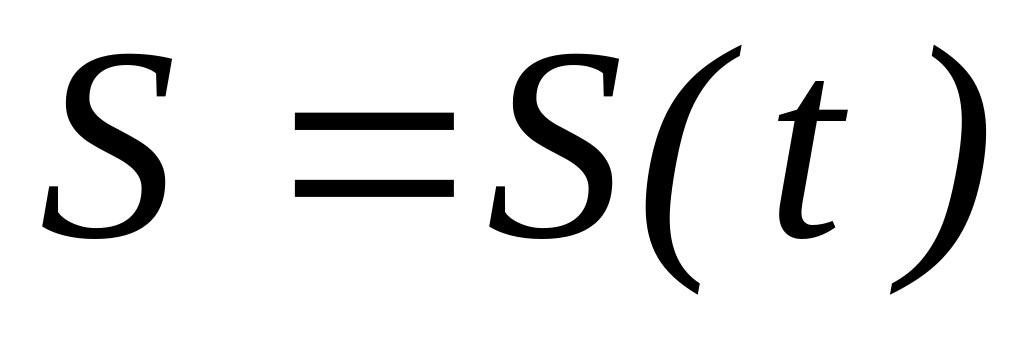 .
.
Первые два пункта разобраны в предыдущей лекции. Покажем, как вычисляется уравнение движения точки, как функция дуговой координаты со временем S(t).
Известно, что если
точка движется в плоскости
![]() ,
элемент дуги
,
элемент дуги
![]() связан
с приращениями координат теоремой
Пифагора, рис. 3.3:
связан
с приращениями координат теоремой
Пифагора, рис. 3.3:
![]()
При
![]() ,
тогда
,
тогда
Дифференциал дуги
![]() связан с дифференциалами функций
связан с дифференциалами функций
![]() и
и
![]() (рис.3.3):
(рис.3.3):
![]() (3.1)
(3.1)
Р |
Интегрируя выражение (3.1), получим уравнение движения точки по криволинейной траектории, как функция времени:
|
Здесь
![]() Если точка
движется в одну сторону, дуговая
координата
Если точка
движется в одну сторону, дуговая
координата
![]() и путь
и путь
![]() ,
пройденный точкой, совпадают. Если точка
меняет направление движения, то путь
,
пройденный точкой, совпадают. Если точка
меняет направление движения, то путь
![]() .
Тогда путь
,
пройденный точкой
вычисляется по формуле (3.12), т.е.
.
Тогда путь
,
пройденный точкой
вычисляется по формуле (3.12), т.е.
![]()
Справка. Для
расстановки пределов интегрирования
в (3.3) нужно исследовать заданную
функцию движения
|
Пример 3.1. Точка М движется прямолинейно, согласно уравнению
![]() (а)
(а)
Вычислить путь , пройденный точкой М за 5с.
Решение. Вычислим направление скорости точки. Имеем:
![]()

Вектор скорости
![]() при
при
![]() меняет направление, поэтому путь
,
пройденный точкой
меняет направление, поэтому путь
,
пройденный точкой
![]() за 5с, будет вычисляться так:
за 5с, будет вычисляться так:

Точка за 5с. прошла
![]()
Пример 3.3. Движение точки М задано уравнением:
![]() (м). (а)
(м). (а)
Вычислить путь , пройденный точкой М за 10 с.
Решение. Вычислим направление скорости точки. Имеем:
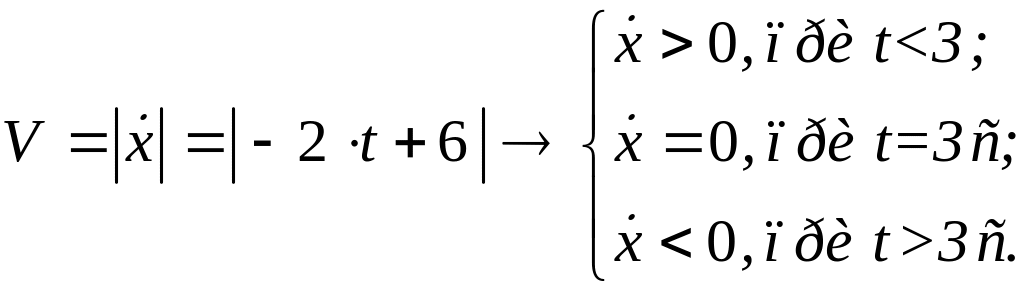 .
.
Вектор скорости
при
![]() с меняет направление, поэтому
путь
с меняет направление, поэтому
путь
![]() ,
пройденный точкой
за 10 с, будет вычисляться так:
,
пройденный точкой
за 10 с, будет вычисляться так:
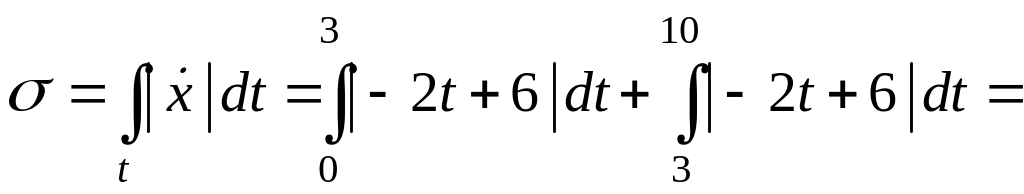
![]()
![]() (м).
(м).

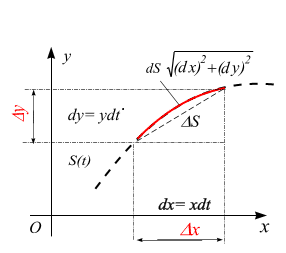 ис.
3.3
ис.
3.3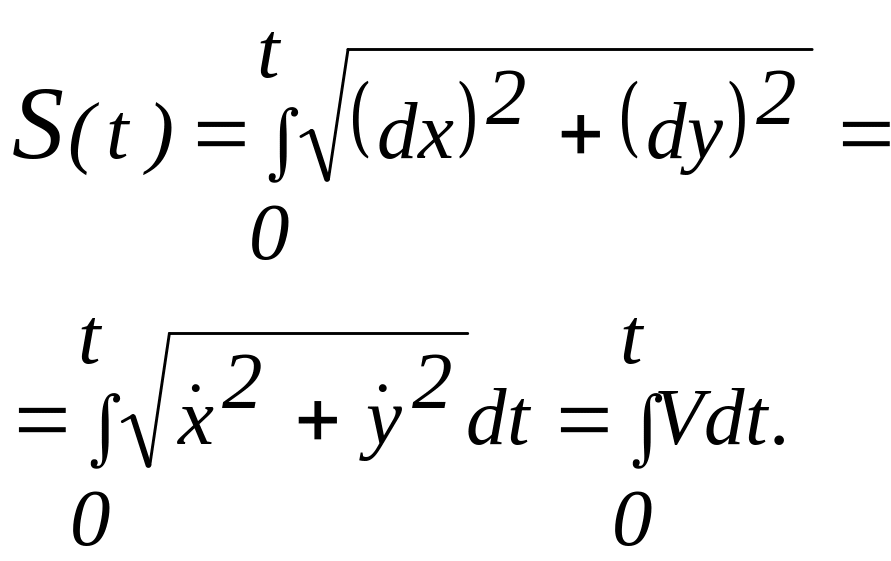 (3.2)
(3.2)