Взяв от обеих частей последнего равенства интегралы с учетом начальных условий, получим

.

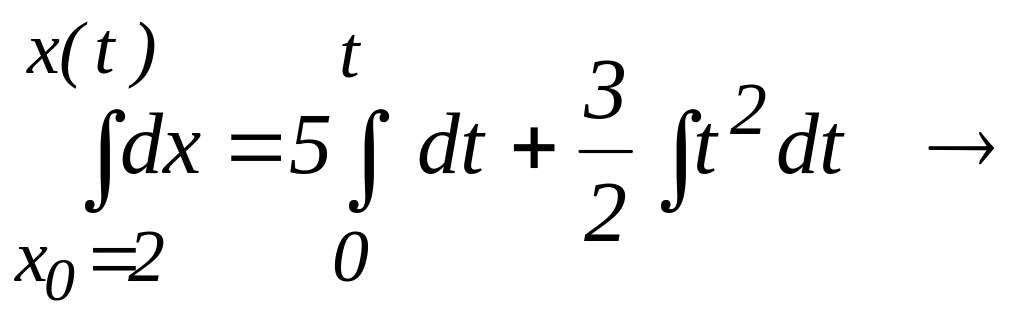
Получили уравнение прямолинейного переменного движения точки.

.

Пример 2.9. Точка движется в плоскости . Уравнение движения точки задано координатным способом:

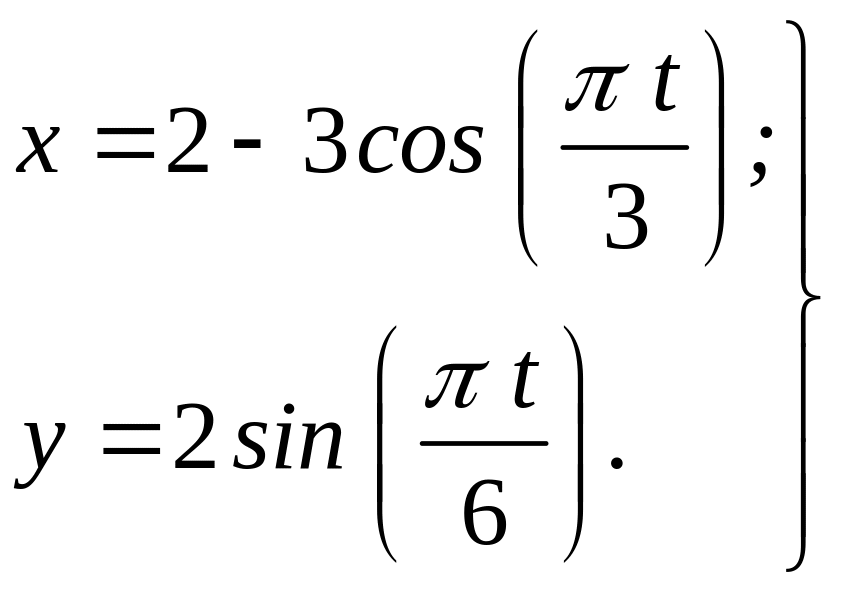, где и выражены в см,  в сек. (а)

Требуется:

Построить и исследовать траекторию движения точки в декартовой системе координат. Вычислить при сек.

1. Положение точки в начальный момент времени 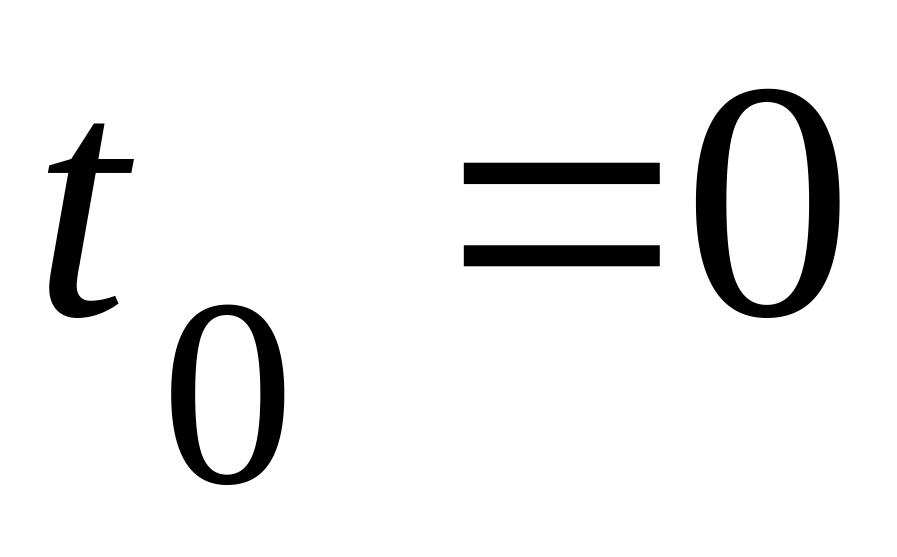, направление движения точки и положение точки на траектории.

2. Вектор скорости _.

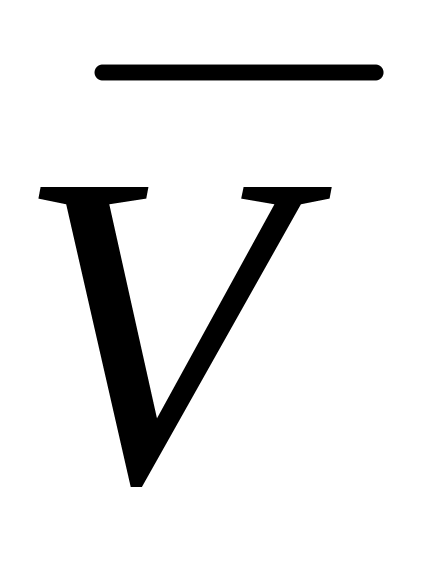3. Вычислить вектор ускорения точки.

4. Вычислить радиус кривизны траектории.

Решение.

Построим траекторию движения точки. Для этого в декартовой системе координат определим область, в которой движется точка, т.е. область значений и . Функции и  ограничены: , , тогда (рис. 2.19):

; .

Получим зависимость . Для этого из уравнений (а) исключим параметр . Введём обозначение , тогда уравнения (а) перепишутся в виде

(б)

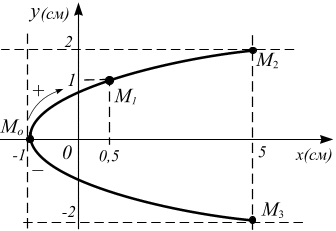
Рис. 2.19

Распишем первое уравнение системы (б), используя формулу двойного угла ( ) и приведем подобные члены:

Из второго уравнения выразим через , получим:

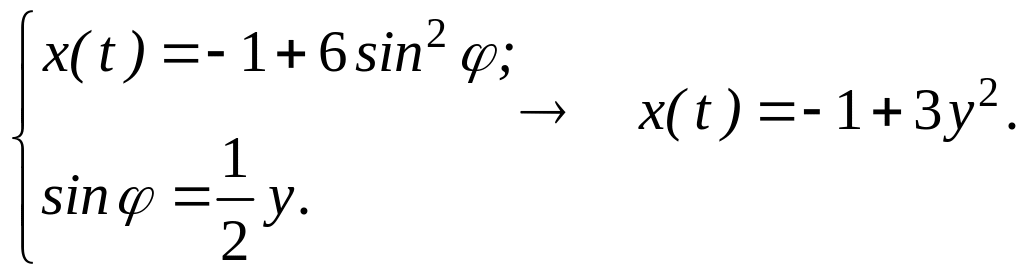(с)

Траекторией точки является парабола с вершиной в точке ; ветви параболы вытянуты вдоль оси (рис. 2.19).

Вычислим координаты точки при :

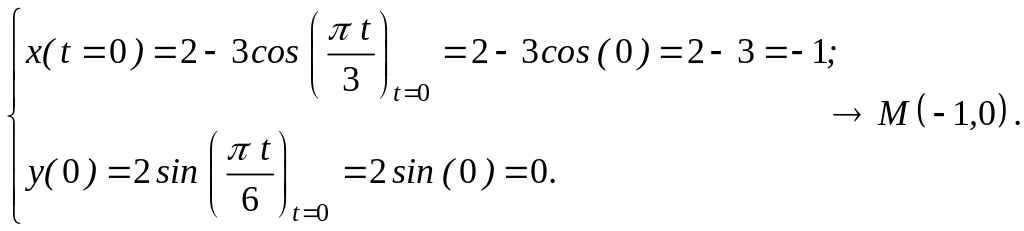
Вычислим время, при котором точка достигает положение

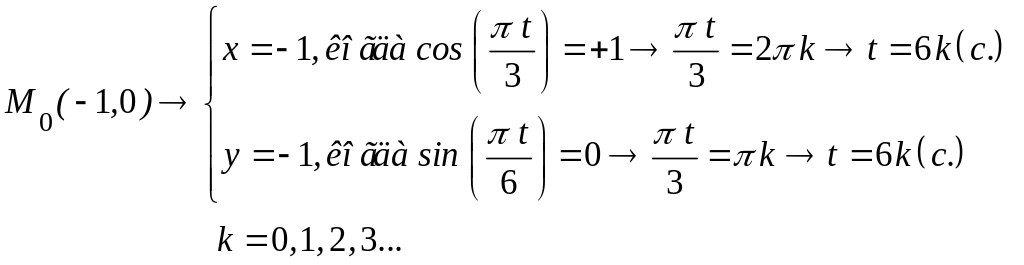
Вычислим координаты точки при :

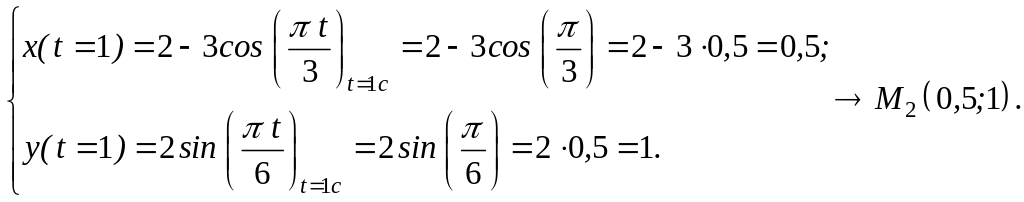
Вычислим время, при котором точка достигает положение

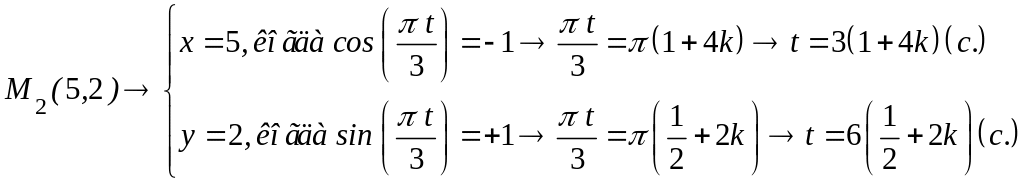
Вычислим время, при котором точка достигает положение

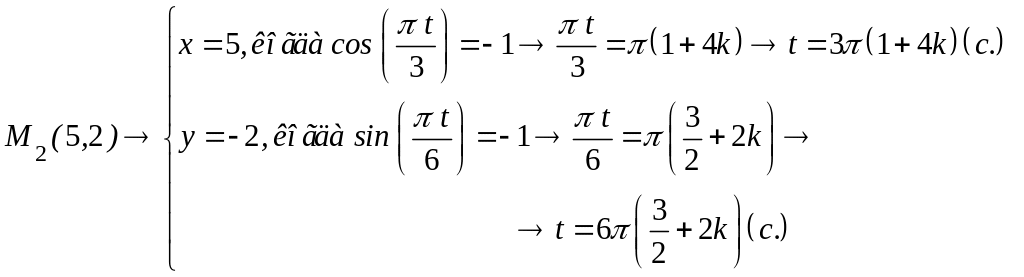
При функции и возрастают, точка М из положения начинает движение по верхней ветви параболы до положения ; далее при точка движется обратно по верхней ветви траектории до точки , и при продолжает движение по нижней ветви параболы до положения , далее при точка возвращается в первоначальное положение т.е. завершает цикл, далее движение повторяется. Время одного цикла движения Точка совершает колебательные движения по параболе.

1. Вычислим скорость точки для с:

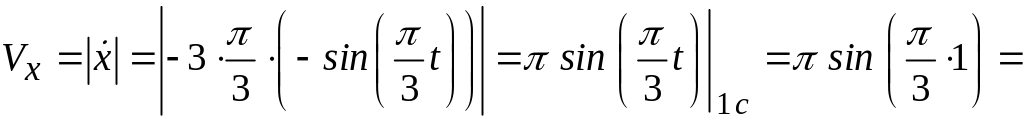
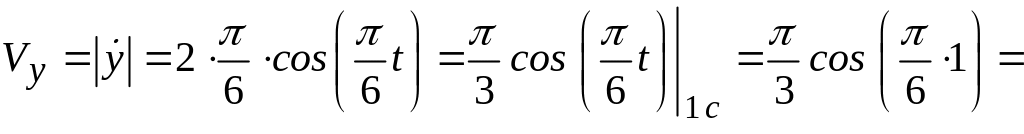
(см/c);

(см/c);

см/с;

, .

Откладываем проекции скорости и вектор на графике (рис. 2.20).

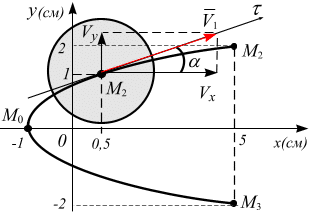
Рис. 2.20

2. Вычислим ускорение точки для с. (рис. 2 21):

(см/c²);

(см/c²);

(см/c²);

,

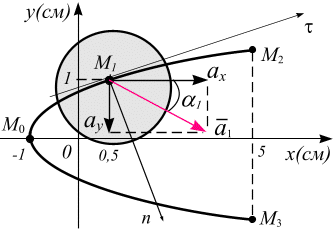
Рис. 2.21

Вектор ускорения точки –  получаем построением параллелограмма на проекциях ускорений и в выбранном масштабе (рис. 2.21).

Как видно из рис. 2.21, вектор полного ускорения точки направлен внутрь вогнутости траектории движения точки.

1 Параграф для самостоятельного изучения.

2 В теории функций одной переменной эта процедура определяет область задания (существования) функций и . Область определения функций в классической кинематике всегда определена – .