- •§ 2. Кинематика точки
- •§ 2. 1. Основные понятия, задачи кинематики
- •§ 2. 2. Векторный способ задания движения точки1
- •§ 2.3. Координатный способ задания движения точки
- •§ 2.4. Прямолинейное движение точки. Прямая и обратная задачи
- •Взяв от обеих частей последнего равенства интегралы с учетом начальных условий, получим
§ 2.3. Координатный способ задания движения точки
Рассмотрим движение точки в плоскости. Пусть Оху – неподвижная декартова система координат. Можно задать значения координат движущейся точки для каждого момента, т. е. задать зависимости
![]() (2.10)
(2.10)
Уравнения (2.10) представляют собой уравнения движения точки в декартовых прямоугольных координатах.
Зная уравнения
(2.10), можно вычислить для каждого момента
времени соответствующие значения x,
y
и, следовательно,
указать положение точки по отношению
к выбранной системе Оxy.
Поэтому уравнения (2.10) являются также
и уравнениями
траектории точки,
заданными параметрически. Для получения
явного вида уравнения траектории, т.е.
зависимости
![]() ,
следует из уравнений (2.10) исключить
параметр t.
,
следует из уравнений (2.10) исключить
параметр t.
Радиус – вектор , если заданы функции (2.10), имеет вид (рис. 2.9)
![]() ,
,
г
Рис. 2.9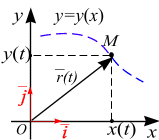
![]() ,
,
![]() – единичные орты системы координат
Оxy.
– единичные орты системы координат
Оxy.
Вектор скорости вычисляется, как производная от по времени, т.е.
![]()
Модуль вектора скорости вычисляется так
![]() , (2.11)
, (2.11)
здесь
![]() ,
,
![]() – проекции скорости
– проекции скорости
![]() на оси
на оси
![]() ,
знак
производных
,
знак
производных
![]() показывает направление проекций скорости
по отношению к соответствующим осям
соответственно.
показывает направление проекций скорости
по отношению к соответствующим осям
соответственно.
Направление вектора скорости вычисляется по направляющим косинусам:
![]() .
(2.11,а)
.
(2.11,а)
Вектор ускорения вычисляется, как вторая производная от по времени, т.е.
![]() .
.
Для вычисления модуля ускорения, имеем
![]() ,
(2.12)
,
(2.12)
где
![]() ,
,
![]() – проекции вектора
на оси
соответственно,
знак производных
– проекции вектора
на оси
соответственно,
знак производных
![]() показывает
направление проекций ускорения по
отношению к осям
.
показывает
направление проекций ускорения по
отношению к осям
.
Направление вектора ускорения вычисляется по направляющим косинусам
![]() .
(2.12,а)
.
(2.12,а)
Рассмотрим движение точки в плоскости. Тогда, уравнения движения точки в декартовых координатах Оху имеют вид:
![]() (2.13)
(2.13)
Уравнения (2.9)
являются также уравнениями траектории
точки, заданными параметрически,
т. е. в системах
координат
![]() и
и
![]() .
.
Уравнение траектории
в явном виде, т. е. в системе координат
![]() .
Для получения этой зависимости,
следует из уравнений (2.13) исключить
параметр
.
Для получения этой зависимости,
следует из уравнений (2.13) исключить
параметр
![]() .Уравнение
траектории в явном виде будет иметь вид
функции
.Уравнение
траектории в явном виде будет иметь вид
функции
![]() .
.
Например, заданы уравнения движения точки:
![]() ,
,
![]() ,
,
в явном виде уравнение движения точки будет иметь вид

Скорость и ускорение точки по модулю и направлению вычисляются по формулам:
|
|
|
Рис. 2.10 |
Пример 2.3.
Положение
кривошипа ОА
в кривошипно-ползунном механизме
(рис. 2.10) определяется углом
|
|
Решение. Декартовую
систему координат
![]() совместим
с точкой О
кривошипа
0А
(рис. 2.11).
Движение
каждой точки данного механизма можно
задать координатным способом относительно
выбранной системы отсчета, т.е. задать
координаты
совместим
с точкой О
кривошипа
0А
(рис. 2.11).
Движение
каждой точки данного механизма можно
задать координатным способом относительно
выбранной системы отсчета, т.е. задать
координаты
![]() и
и
![]() каждой точки.
каждой точки.
Вычислим положение
механизма при
![]() с, которое
определяется углом
с, которое
определяется углом
![]() .
Имеем:
.
Имеем:
 .
.
Точка А движется
по окружности, радиус которой равен
длине кривошипа ОА, точка В –
прямолинейно вдоль оси
![]() .
Следовательно, в любой момент времени
положение точки А определяется
координатами
.
Следовательно, в любой момент времени
положение точки А определяется
координатами
![]() ,
а движение точки В определяться
координатой
,
а движение точки В определяться
координатой
![]() (рис. 2.11).
(рис. 2.11).
|
Имеем:
|
Скорость и ускорения точки А (рис. 1.3, а):
Скорость точки А:


![]() (м/c).
(м/c).
а |
|
б |
б
|
|
Рис. 2.12 |
||||
Направление вектора скорости:

![]() .
.
Ускорение точки А (рис. 2.12, б):
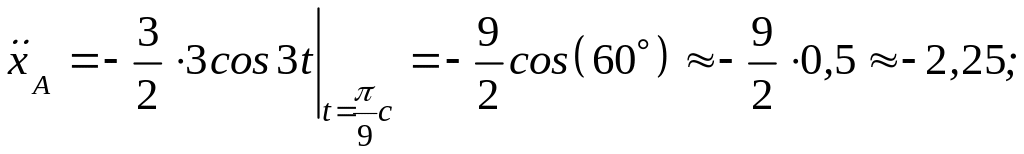

![]() (м/c).
(м/c).
Имеем:

![]() точка А
вдоль оси
движется ускоренно;
точка А
вдоль оси
движется ускоренно;
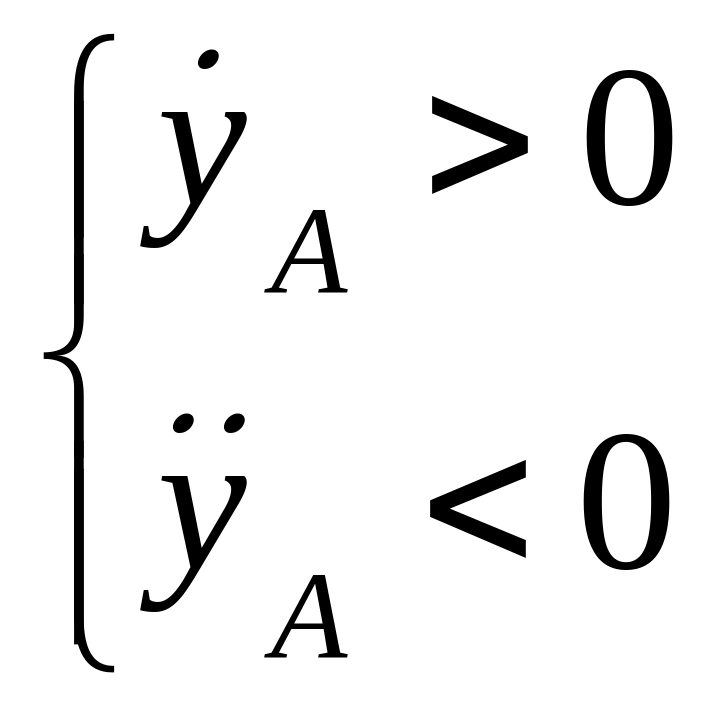 точка А
вдоль оси
точка А
вдоль оси
![]() движется замедленно.
движется замедленно.
Направление вектора ускорения:
![]()
![]() .
.
Скорость точки и ускорение В (рис. 2.12, а, б)
![]() м/c;
м/c;
![]() м/c2
м/c2
 точка В
движется против оси
ускоренно.
точка В
движется против оси
ускоренно.
Пример 2.4. Движение точки M по плоскости Оху задано уравнениями движения
![]() .
(а)
.
(а)
Построить траекторию
движущейся точки, вычислить
скорость и ускорение точки в моменты
времени
![]() и
и
![]() .
.
Решение.
Для
построения
траектории движущейся точки в декартовой
системе координат определим область,
в которой движется точка, т.е. область
значений
![]() и
и
![]() .2
Функции
.2
Функции
![]() и
и
![]()
ограничены, т.е.
ограничены, т.е.
![]() ,
,
![]() ,
получаем:
,
получаем:
![]()
Выделяем на координатной плоскости область, ограниченную полученными неравенствами, за эту область точка при движении не выходит (рис. 2.10). Исключим параметр t из уравнений движения (a). Для этого делим первое уравнение на 2, второе – на 4, возводим их в квадрат и складываем между собой:

![]() .
.
|
Учитывая, что
Траекторией
движущейся точки является эллипс
(рис. 2.13). Подставляя в (а) значение
|
Точка в начальный
момент времени занимает положение
![]() .
Определим направление движения точки.
Уравнения движения (а) заданы возрастающей
функцией
.
Определим направление движения точки.
Уравнения движения (а) заданы возрастающей
функцией
![]() и убывающей функцией
и убывающей функцией
![]() ,
поэтому при увеличении t
координата «
,
поэтому при увеличении t
координата «![]() »
возрастает, а «у»
убывает, следовательно, точка движется
по эллипсу по часовой стрелке.
»
возрастает, а «у»
убывает, следовательно, точка движется
по эллипсу по часовой стрелке.
Вычислим модуль и направление вектора скорости точки М. Имеем:
 (в)
(в)
Вычислим модуль и направление вектора ускорения точки М. Имеем:
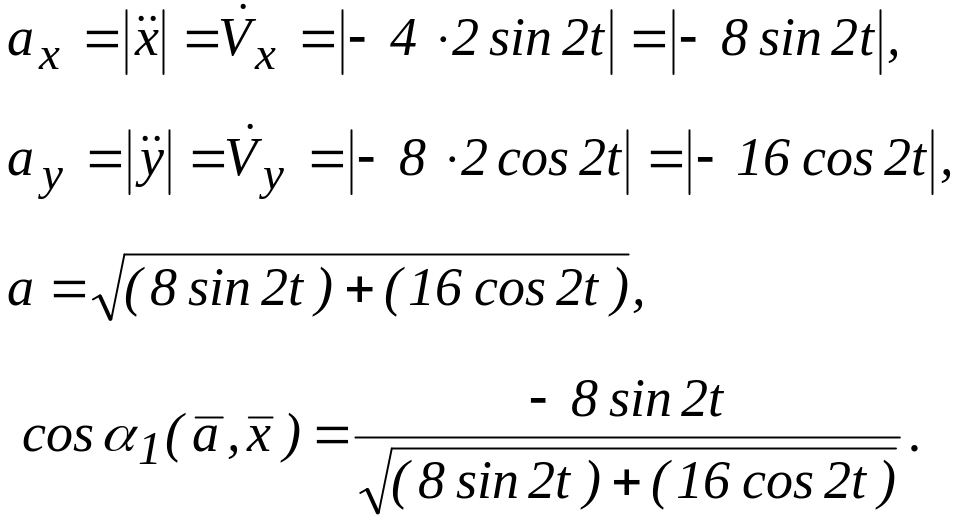 (г)
(г)
При
![]() из (а) получаем, что точка М
имеет координаты х=2,
у=0, т.е.
занимает положение
из (а) получаем, что точка М
имеет координаты х=2,
у=0, т.е.
занимает положение
![]() (рис. 2.13). Подставляя в (в) и (г) время
,
получим
(рис. 2.13). Подставляя в (в) и (г) время
,
получим
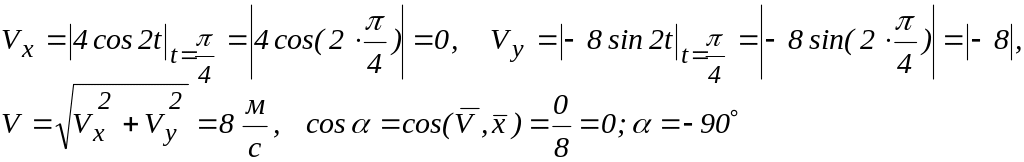

Откладываем значение скорости (рис. 2.14, а) и ускорения (рис. 2.14, б) точки на траектории.
Рис.
2.14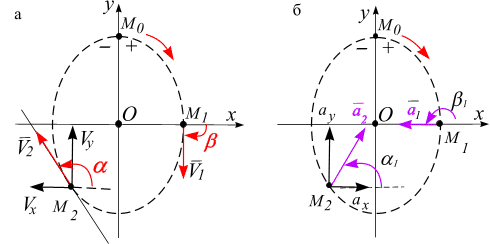
При
![]() из (а) получаем, координаты точки
из (а) получаем, координаты точки
![]() :
:![]() -
-![]() ,
(рис. 2.14).
,
(рис. 2.14).
Вычислим, используя (в) и (г), модуль и направление векторов скорости и ускорения.
Имеем:
![]()
![]()
![]()
![]()
![]()
для ускорения
![]()
![]()
![]()
![]() ,
,
![]() .
.
Откладываем значение скорости (рис. 2.14, а) и ускорения (рис. 2.14, б) точки на траектории.
П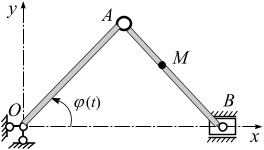 ример
2.5.
Положение
кривошипа ОА
кривошипно-ползунного механизма
(рис.
2.12), определено углом
(рад).
Вычислить скорость и ускорение точки
ример
2.5.
Положение
кривошипа ОА
кривошипно-ползунного механизма
(рис.
2.12), определено углом
(рад).
Вычислить скорость и ускорение точки
![]() и точки
и точки
![]() в момент
времени
в момент
времени
![]() с, если
с, если
Рис. 2.15 ![]() см,
см,
![]() .
.
Решение. Совместим
декартовую систему координат
![]() с точкой
О кривошипа
ОА (рис.
2.16).
с точкой
О кривошипа
ОА (рис.
2.16).
Движение каждой
точки данного механизма можно задать
координатным способом. Положение каждой
точки механизма в системе
будет
определено двумя координатами: для
точки
![]() и
и
![]() для точки
для точки
![]() и
и
![]() .
.
Вычислим положение
механизма и координаты точек
и
при
![]() (рис. 2.16).
(рис. 2.16).
Имеем:
![]() (
(![]() ).
).
Справка:
|
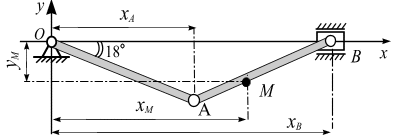
Рис. 2.16
Координаты точки М :

![]()
Координата точки
(![]() ):
):
![]()
Скорость и ускорение точки М (рис. 2.17).
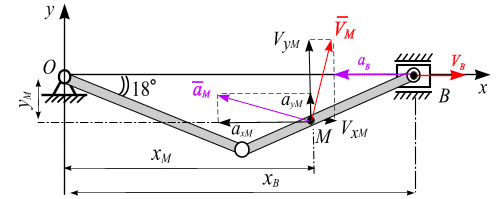
Рис. 2.17
Скорость точки М
для
![]() с:
с:
![]()
![]()
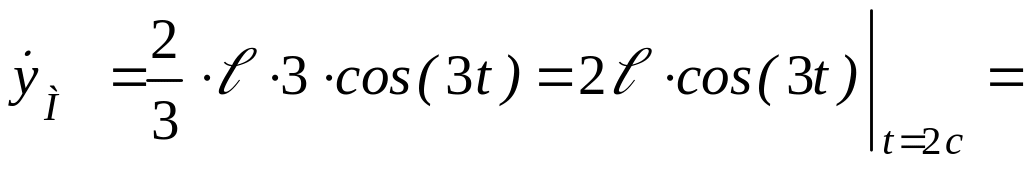
![]() ;
;
![]() (м/c).
(м/c).
Справка: Формулы приведения:
|
Ускорение точки М для с:


![]() (м/c2).
(м/c2).
Имеем:
![]() точка
М
вдоль оси
движется замедленно;
точка
М
вдоль оси
движется замедленно;
![]()
![]() точка М
вдоль оси
движется ускоренно.
точка М
вдоль оси
движется ускоренно.
Скорость и
ускорение точки В
(рис. 2.17).
Точка движется прямолинейно вдоль оси
.
Следовательно, в любой момент времени
координата
![]() ,
и движение этой точки будет определяться
только координатой
.
,
и движение этой точки будет определяться
только координатой
.
Имеем:
Скорость точки В:
![]()
![]() м/с;
м/с;
Ускорение точки В:
![]()
![]() м/с2.
м/с2.
Имеем
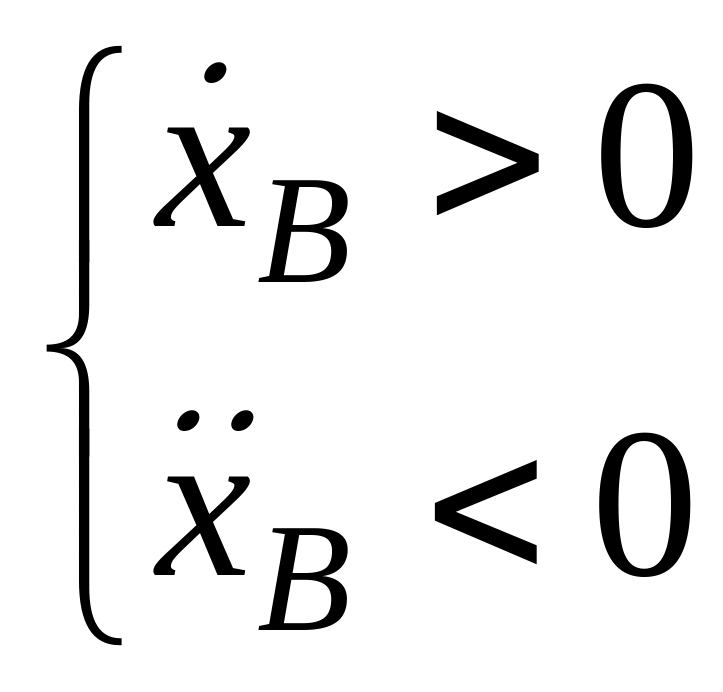 точка
В
движется замедленно.
точка
В
движется замедленно.

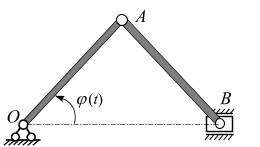
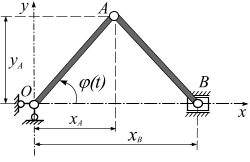 Рис.
2.11
Рис.
2.11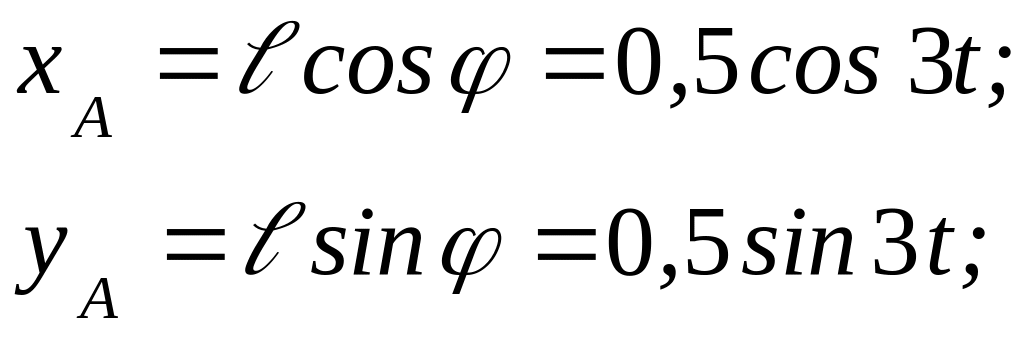
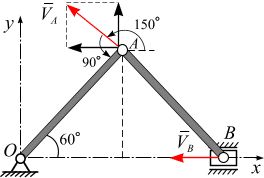
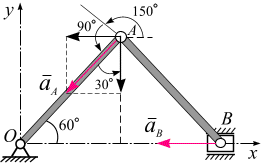
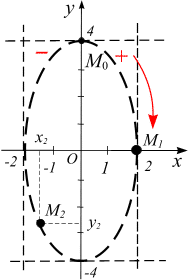 Рис.
2.13
Рис.
2.13