- •§ 2. Кинематика точки
- •§ 2. 1. Основные понятия, задачи кинематики
- •§ 2. 2. Векторный способ задания движения точки1
- •§ 2.3. Координатный способ задания движения точки
- •§ 2.4. Прямолинейное движение точки. Прямая и обратная задачи
- •Взяв от обеих частей последнего равенства интегралы с учетом начальных условий, получим
§ 2. 2. Векторный способ задания движения точки1
Движение точки
задается радиус–
вектором
![]() этой точки. Движение точки считается
заданным, если известен радиус – вектор
движущейся точки как функция времени,
т.е.
этой точки. Движение точки считается
заданным, если известен радиус – вектор
движущейся точки как функция времени,
т.е.
![]() .
(2.5)
.
(2.5)
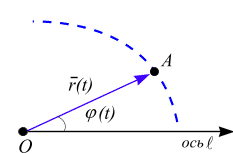
Рис. 2.5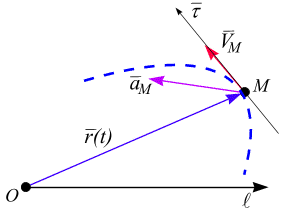
Пусть
![]() задает движение точки М,
тогда при изменении t
точка опишет
кривую в пространстве (рис. 2.5). Эта кривая
называется годографом радиус-вектора
и соответствует
траектории
точки.
задает движение точки М,
тогда при изменении t
точка опишет
кривую в пространстве (рис. 2.5). Эта кривая
называется годографом радиус-вектора
и соответствует
траектории
точки.
Вектор скорости
направлен по касательной к траектории
в точке
![]() –
–![]() (рис. 2.4) и вычисляется по формуле
(рис. 2.4) и вычисляется по формуле
![]() .
(2.6)
.
(2.6)
Вектор ускорения направлен внутрь вогнутости траектории в точке и вычисляется по формуле:
![]() . (2.7)
. (2.7)
Покажем технологию вычисления скорости и ускорения точки А.
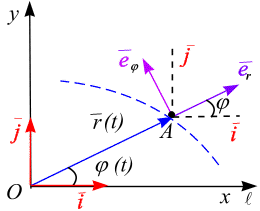
Пусть движение
точки А происходит в заданной
плоскости. Зададим радиус – вектор
движущейся точки как функция времени
т.е. зададим функции
![]() ,
,
![]() ,
рис.2.6, а
,
рис.2.6, а
а
|
б |
|
Рис. 2.6
Совместим начало
декартовой системы координат и ось
![]() с полюсом
с полюсом
![]() и полярной осью
и полярной осью
![]() ,
соответственно (рис. 2.6, б). Радиус –
вектор
,
соответственно (рис. 2.6, б). Радиус –
вектор
![]() разложим по единичным ортам
разложим по единичным ортам
![]() ,
,
![]() :
:
![]() .
.
Введем
![]() - единичный вектор, направленный вдоль
радиус-вектора
- единичный вектор, направленный вдоль
радиус-вектора
![]() в сторону возрастания модуля
в сторону возрастания модуля
![]() ,
и
,
и
![]() - единичный вектор, получающийся из
поворотом последнего на угол
- единичный вектор, получающийся из
поворотом последнего на угол
![]() против часовой стрелки. Единичные
векторы
и
задают направления двух взаимно
перпендикулярных осей. Ось, направление
которой определено единичным вектором
называется радиальной,
а единичным вектором
– трансверсальной.
В системе
координат Оху
векторы
и
можно связать с единичными ортами
против часовой стрелки. Единичные
векторы
и
задают направления двух взаимно
перпендикулярных осей. Ось, направление
которой определено единичным вектором
называется радиальной,
а единичным вектором
– трансверсальной.
В системе
координат Оху
векторы
и
можно связать с единичными ортами
![]() следующим образом (рис.2.6, б):
следующим образом (рис.2.6, б):
![]() ,
,
![]() .
.
Вычислим скорость точки А. Так как
![]() ,
,
![]() ,
,
имеем

![]() .
.
Модуль скорости
![]() .
(2.8)
.
(2.8)
Проекции скорости
на
радиальную ось -![]() и
трансверсальную ось -
и
трансверсальную ось -![]() и называются соответственно радиальной
и трансверсальной скоростями.
и называются соответственно радиальной
и трансверсальной скоростями.
Угол, образованный вектором скорости с положительным радиальным направлением, вычисляется по формуле
![]() .
.
Для ускорения аналогично получаем:


![]() .
.
Тогда модуль ускорения
![]() , .
(2.9)
, .
(2.9)
Проекции ускорения
![]() на
радиальную ось -
на
радиальную ось -![]() и трансверсальную ось -
и трансверсальную ось -![]() называются радиальным
и трансверсальным ускорениями
соответственно. Угол, образованный
вектором ускорения с положительным
радиальным направлением, вычисляется
по формуле
называются радиальным
и трансверсальным ускорениями
соответственно. Угол, образованный
вектором ускорения с положительным
радиальным направлением, вычисляется
по формуле
![]() .
.
Движение задано радиус-вектором , тогда
|
Пример 2.1. Движение точки задано радиус-вектором :
![]() (а)
(а)
Построить траекторию,
вычислить скорость и ускорение точки
для моментов времени
![]() ,
,
![]()
Решение.
Исключая из уравнений движения (а)
параметр t,
получим уравнение траектории в полярных
координатах: r=.
Это уравнение
описывает движение точки А
по лучу![]() ,
вращающемуся около полюса О.
Траектория такого движения называется
спиралью Архимеда (рис. 2.7).
,
вращающемуся около полюса О.
Траектория такого движения называется
спиралью Архимеда (рис. 2.7).
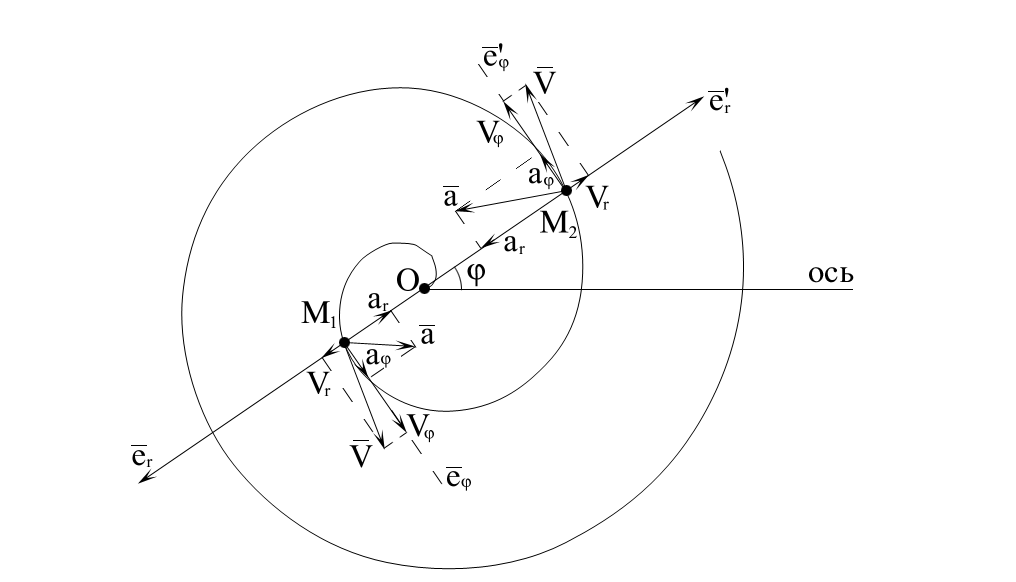
Рис. 2.7
Точка при
занимает положение
![]() с координатами:
с координатами:
![]() (
(![]() ).
).
Точка при
занимает положение
![]() с координатами:
с координатами:
![]()
Проекции скорости и ускорений на полярные оси вычислим по формулам:
![]() ;
;
![]() .
.
Вычислим скорость
и ускорение точки при
![]() :
:
![]() ;
;
![]() .
.
Вычислим скорость
и ускорение точки при
![]() :
:
![]() ;
;
![]() .
.
Пример 2.2. Движение точки задано в уравнением
![]() .
.
Построить траекторию
движущейся точки и вычислить ее скорость
при
![]()
Решение. Построить траекторию движущейся точки – это значит построить годограф радиус – вектора. Для построения годографа составим таблицу 2.1 точек годографа для отдельных значений t.
Табл. 2.1
t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Для любой точки
годографа имеем:
![]() ,
,
![]() ,
,
![]() ,
поэтому при любом t
выполняется
равенство х2+у2=а2,
т.е. все точки годографа лежат на цилиндре,
направляющей которого является окружность
в плоскости переменных х,
у, а образующая
параллельна оси
,
поэтому при любом t
выполняется
равенство х2+у2=а2,
т.е. все точки годографа лежат на цилиндре,
направляющей которого является окружность
в плоскости переменных х,
у, а образующая
параллельна оси
![]() .
Искомый годограф имеет вид, изображенный
на рис. 2.8 a,
и называется винтовой
линией.
.
Искомый годограф имеет вид, изображенный
на рис. 2.8 a,
и называется винтовой
линией.
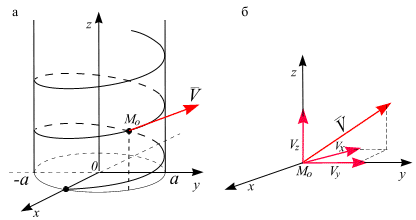
Рис. 2.8
Вычислим положение точки при заданном времени.
Точка МО
при
![]() имеет координаты:
имеет координаты:
![]() ,
,
![]() ,
,
![]() .
.
Вычислим скорость точки для текущего времени:
![]() .
.
При
![]() ,
рис. 2.8, б:
,
рис. 2.8, б:
![]()