62

§ 2. Кинематика точки

Содержание: задачи кинематики; траектория, скорость, ускорение точки. Векторный способ задания движения точки. Векторы скорости и ускорения точки (годограф скорости). Примеры. Скорость и ускорение точки в полярных координатах. Координатный способ задания движения. Определение скорости и ускорения точек по их проекциям на координатные оси.

§ 2. 1. Основные понятия, задачи кинематики

Задачи кинематики состоят в определении способов задания движения материальной точки, твердого тела и механической системы, также методов вычисления скорости и ускорения точки (или точек твердого тела, механической системы).

Задать движение материальной точки или твердого тела (точек механической системы)  это значит задать способ вычисления положения точки или течек твердого тела (точек механической системы) в любой момент времени.

Траектория точки. Геометрическое место последовательных положений движущейся точки в декартовой системе координат называется траекторией. Если в интервале времени траектория прямая линия, то движение в этом интервале называется прямолинейным, в противном случае – движение называется криволинейным (рис. 2.1).

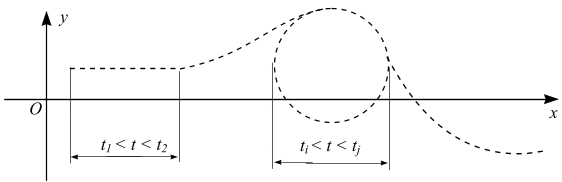
Рис. 2.1

В частности, движение точки на интервале времени называют круговым, если на этом интервале точка движется по окружности.

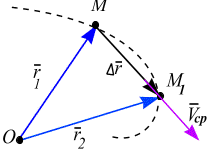
Скорость точки. Пусть положение движущейся точки М относительно произвольно выбранного неподвижного центра О определяется в момент

а		времени t радиус– вектором , который соединяет движущуюся точку М с центром О, (рис. 2.2, а). В следующий момент времени положение точки (точка М1) определяется радиус–вектором . За время , радиус-вектор изменится на . Средней скоростью точки за время называют соотношение , т.е. (2.1)
б	Рис. 2.2

Средняя скорость параллельна вектору и не имеет точки приложения (рис. 2.2, а).

Мгновенная скорость точки в момент времени t определяется как предел средней скорости при Δt → 0, т.е.

. (2.2)

Производная по времени от функций обозначается точкой над символом этой функции, а вторая производная – двумя точками.

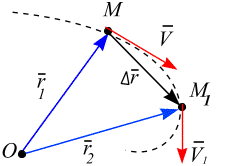
Вектор скорости приложен в точке М, направлен в сторону ее движения по предельному направлению вектора → 0, т.е. совпадает с касательной к траектории в точке М (рис. 2.2, б). Размерность скорости в СИ: = длина/время = м/с. Часто скорость выражают в км/ч = 0,28 м/с.

Скорость - это векторная величина, характеризующая быстроту и направление движения точки

Ускорение точки. Пусть движущаяся точка М в момент времени t имеет скорость (рис. 2.2). В момент времени = t + Δt эта точка занимает положение М₁, имея скорость . Чтобы изобразить приращение скорости за время Δt, перенесем вектор скорости параллельно самому себе в точку М, тогда .

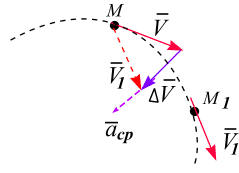
а		Средним ускорением точки за время Δt называется отношение , т.е. . (2.3) Вектор совпадает с направлением вектора , т.е направлен внутрь вогнутости траектории (рис. 2.3, а). Ускорением точки в момент времени t называют предел, к которому стремится среднее ускорение при Δt → 0, т.е. . (2.4)
б
Рис. 2. 3

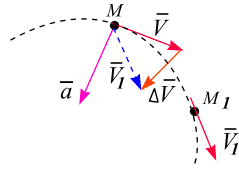
Вектор ускорения всегда направлен внутрь вогнутости под любым углом к касательной к траектории движения (рис. 2.3, 6). Размерность ускорения в СИ: = длина/время² = м/с².

Ускорение – векторная величина, которая характеризует быстроту изменения модуля и направления вектора скорости.

Вопрос о скорости был “камнем преткновения” до начала ньютоновской эпохи в механике. Задачи на вычисление скорости движения какого-либо тела тогда были неразрешимы. Кроме того, существовали многочисленные «парадоксы». Один из них придуман Зеноном, он хорошо показывает, насколько была сложна до Ньютона проблема вычисления и определения скорости движения. Зенон – греческий философ и астроном, живший на о. Кипр около 336-264 до н.э., известный еще и тем, что одним из первых правильно объяснил затмение солнца и луны.

«

Рис. 2.4

Предположим, – говорил он, – что Ахиллес (рис. 2.3, точка ) бегает в десять раз быстрее черепахи (рис. 2.4, точка ). Тем не менее, Ахиллес никогда не перегонит черепаху. Действительно, пусть в начале состязания черепаха находилась в 100 метрах впереди Ахиллеса . Тогда ко времени, когда Ахиллес пробежит эти 100 метров, черепаха окажется в 10 метрах впереди него. Пробежав и эти 10 метров, Ахиллес увидит черепаху в 1-ом метре впереди себя. За то время, пока он пробежит этот метр, черепаха пройдет 10 сантиметров и т.д. до бесконечности. Следовательно, в любой момент черепаха будет впереди Ахиллеса, и он когда не сможет перегнать».

Для разрешения этого парадокса была высказана новая идея независимо Ньютоном и Лейбницем, которая положила начало новой области математики, помимо хорошо изученных учеными в те времена геометрии и алгебры. Для описания движения Ньютон ввел параметр , назвал его абсолютным временем и стал рассматривать путь, пройденный Ахиллесом и черепахой в единицу времени, т.е. рассматривать движение в плоскости с координатами (рис. 2.4). За одно и тоже время Ахиллес пройдет путь (точка ), а черепаха (точка ), причем . Соединяя полученные точки ( ) и ( ) в плоскости ( ), получим две прямые под разными углами к оси t. Очевидно, что если угол наклона прямой (1) – угол , будет больше угла наклона кривой (2) – угол , то Ахиллес перегонит черепаху в момент времени , когда прямые (1) и (2) пересекутся.

Новая идея заключалась в том, чтобы малые расстояния (путь ) рассматривать на соответствующих малых отрезках времени и посмотреть, что произойдет с частным, если отрезок времени брать все меньше и меньше. Иными словами, брать предел отношения пройденного расстояния к интервалу времени при неограниченном уменьшении последнего. Тогда, скорость движения Ахиллеса и скорость движения черепахи определятся через углы наклона прямых и (рис. 2.4) следующим образом

	. Путь , пройденный точкой, зависит от времени, следовательно, является функцией времени, т.е. . Предел был назван производной от функции . Исаак Ньютон (Newton, Isaac) (1643-1727) и Лейбниц Готфрид Вильгельм (Leibniz, Gottfried Wilhelm von) (1646–1716), заложили основы новой области математики – дифференциального и интегрального исчисления.
Исаак Ньютон
Г. В. Лейбниц