2. Проектирование схемы нивелирных ходов

Запроектированная система нивелирных ходов должна быть оптимальной как с точки зрения обеспечения необходимой точности измерений, так и с учётом минимизации затрат на выполнение работ. При этом в любом случае должна обеспечиваться непрерывная связь всех деформационных знаков со всеми исходными знаками (за исключением редких случаев). Следует также, по возможности, на каждом из отдельных объектов образовать замкнутый нивелирный ход.

При предварительных оценках качественных характеристик схемы нивелирных ходов связи между отдельными системами ходов, например, 12=13, 10=15 (рис. 2) следует оптимизировать. Увеличивать количество связей следует только при необходимости.

Так, на рис. 2 представлен проект нивелирных ходов, представляющих собой два замкнутых нивелирных хода:

1-2(3)-4-5-6(7)-8-9-10-11-12-1 и 13-14-15-16-17-18-19-20-13. Запроектированы связи 12=13 и 10=15. Привязка осуществляется висячими ходами Р1=12 и Р2=19.

Следует иметь в виду, что парные точки 2(3) и 6(7) наблюдаются с двух соседних станций как одна точка, но рейку устанавливают обязательно на каждую из них.

На рис. 3 представлена схема нивелирных ходов с указанием рабочих секций, необходимость в которых (введением «иксовых» точек) проявилась в результате рекогносцировки местности и фактического положения установленных на объектах деформационных и исходных знаков. Так, при обеспечении связи деформационных знаков 4-5, 9-10, 16-17 в замкнутых ходах выявилась необходимость использования дополнительных «иксовых» точек Х1, Х2 и Х3. При обеспечении связей Р1-12 и Р2-19 используются «иксовые» точки Х4, Х5, Х6, Х7 и Х8.

На схеме указано три замкнутых полигона, А, Б и В. На самом деле их можно представить и больше, например, объединить полигоны А и Б и т.п. Обычно на первом этапе на схемах рассматривают минимально возможные замкнутые системы нивелирных ходов.

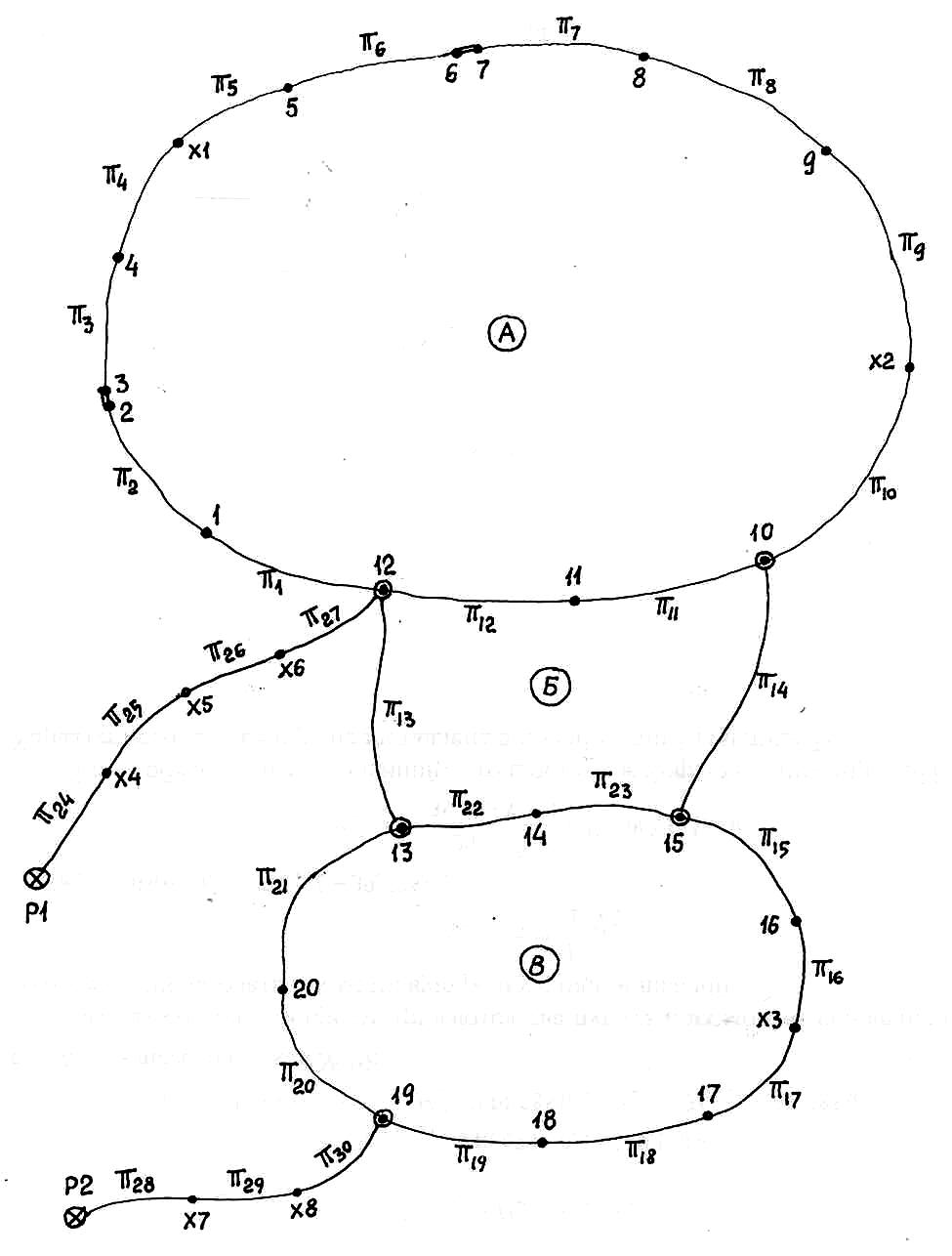
Рис. 3. Схема нивелирных ходов

• - деформационные знаки; то же в кружке – деформационные узловые знаки;

А, Б, В – замкнутые нивелирные полигоны

Кроме указанных обозначений на схеме введены обозначения качественных характеристик секций значком π. О качественных характеристиках рассказано в следующем разделе.

3.Оценка качественных характеристик нивелирных секций и поиск слабоопределяемой точки

3.1. Вычисление качественных характеристик секций

Секцией является отдельный фрагмент нивелирного хода, опирающийся либо на два соседних деформационных знака, наблюдаемых с одной станции, либо на две узловых точки, связь между которым осуществляется по одной нивелирной линии. Например (рис. 3), секции 12-1, 1-2(3), Х3-17 между деформационными знаками. Или секция 19-13 между узловыми точками.

Качественной характеристикой схемы, секции и т.п. является вес данного элемента Р или обратный вес этого элемента

. (1)

Вес элемента может быть оценен по формуле

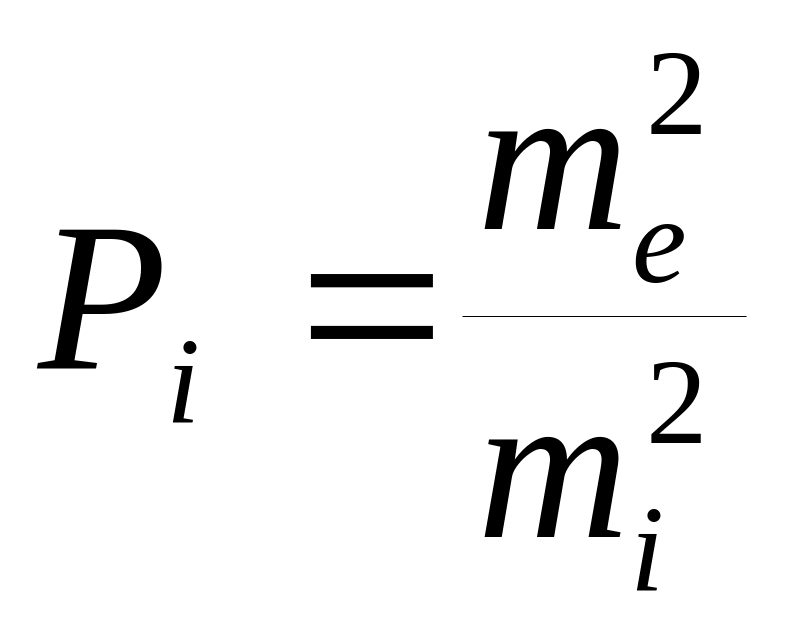, (2)

где m_e – средняя квадратическая погрешность (СКП) единицы веса; m_i – СКП определения превышения на станции.

В результате исследования нивелиров установлено, что

, (3)

где D_i – расстояние от нивелира до рейки (плечо на станции геометрического нивелирования), в метрах; К_Н – коэффициент погрешности отсчёта для нивелира соответствующего класса (см. табл.1).

Таблица 1

Нивелир	Н-05	Н-1	Н-2	Н-3
КН, мм/м	0,010	0,015	0,025	0,050

Формула (3) практически имеет линейный вид до расстояний 30 м.

С учётом (3) формулу (2) можно записать в виде

, (4)

где D_e – величина плеча на станции, вес которой равен единице.

Единицей веса превышения удобно брать превышение, измеренное на станции: при одном горизонте прибора; в ходе одного направления; по двухшкальной рейке; при плече, равном D_e. Либо превышение, измеренное на станции: при двух горизонтах прибора; в ходе одного направления; по одношкальной рейке; при плече, равном D_e.

В этом случае погрешность превышения на станции будет равна погрешности отсчёта по рейке, т.е.,

, (5)

или

, (6)

или, для единицы веса,

(7)

Значение качественной характеристики π, как это следует из (4), равно

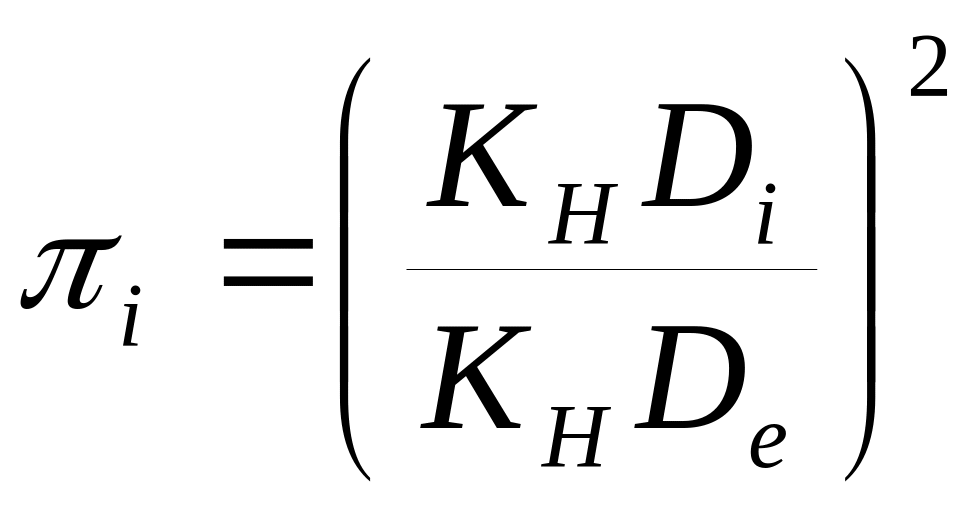(8)

По схеме размещения деформационных знаков совместно с системой нивелирных ходов (рис. 2), выполненной в соответствующем масштабе, оценивают значения плеч на станциях. При оценке величины плеча следует руководствоваться тем, что нивелир можно устанавливать от стены сооружения не ближе, практически, 3-5 м от неё. В этом случае длина плеча может быть оценена как

, (9)

где L – расстояние между наблюдаемыми точками на станции геометрического нивелирования.

При этом следует иметь в виду, что при благоприятных условиях, например, в секции 10-15 (рис. 2), значения плеч можно принять равными половине расстояния между точками.

В таблице 2 приведены полученные значения плеч на станциях (в секциях), а также значения качественных характеристик π, вычисленные по формуле (8). В формуле (8) величину D_e оценивают как среднее арифметическое по текущим значениям плеч, относящихся непосредственно к объектам (без учёта привязки):

. (10)

Значения D_i округляют до 1 м. Величину D_e можно оставить целой либо округлить до 0,5 м. В примере (табл. 2):

м (для первых двадцати трех секций);

D_e = 170/23 = 7,39 м = 7,5 м.

Полученные значения π округляют до 0,01.

После получения D_e следует запроектировать секции в ходах привязки. При этом длину плеча в секции не рекомендуется делать больше 20-25 м. В табл. 2 указанные характеристики даны в значениях π₂₄ – π₃₀ .

Таблица 2

Значения качественных характеристик секций нивелирных ходов

Секция	Плечо Di, м	πi	Значение πi	Секция	Плечо Di, м	πi	Значение πi
12-1	10	π1	1,78	16-Х3	5	π16	0,44
1-2(3)	6	π2	0,64	Х3-17	4	π17	0,28
2(3)-4	6	π3	0,64	17-18	7	π18	0,87
4-Х1	5	π4	0,44	18-19	7	π19	0,87
Х1-5	6	π5	0,64	19-20	10	π20	1,78
5-6(7)	5	π6	0,44	20-13	10	π21	1,78
6(7)-8	7	π7	0,87	13-14	6	π22	0,64
8-9	8	π8	1,14	14-15	6	π23	0,64
9-Х2	10	π9	1,78	Р1-Х4	15	π24	4,00
Х2-10	6	π10	0,64	Х4-Х5	8	π25	1,14
10-11	8	π11	1,14	Х5-Х6	10	π26	1,78
11-12	8	π12	1,14	Х6-12	12	π27	2,56
12-13	17	π13	5,14	Р2-Х7	12	π28	2,56
10-15	4	π14	0,28	Х7-Х8	10	π20	1,78
15-16	9	π15	1,44	Х8-19	15	π30	4,00

Вообще говоря, можно было принять для D_e и 7 м, и 8 м, и 10 м. От этого выводы при анализе схемы нивелирных ходов не изменятся. Для удобства следует стремиться к тому, чтобы значения весов (и обратных весов) были сравнительно близки к единице. Так проще для расчетов. Хотя, как следует из таблицы 2, получились и секции со значениями качественных характеристик, значительно превышающих единицу (секция 12-13) либо значительно меньше единицы (секция Х3-17). Для отдельных секций это допустимо.

3.2. Эквивалентные преобразования в нивелирных ходах

При анализе геодезических построений используют т.н. эквивалентные преобразования, в результате чего получается эквивалентный ход, идентичный по своим характеристикам преобразованному, но имеющий более простую либо более сложную форму.

Рассмотрим указанные преобразования для нивелирных ходов.

На рис. 4 показаны различные виды нивелирных ходов простейшей формы и эквивалентные им ходы.

Качественная характеристика секции между узловыми точками А и В (рис. 4, а) определяется суммой значений качественных характеристик составляющих секций:

(11)

Если между узловыми точками существует две или несколько систем параллельных ходов (рис. 4, б), то качественная характеристика секции, эквивалентной двум ходам, определяется по формуле

, (12)

где П = π₁ + π₂.

Для нескольких ходов решение задачи выполняется последовательно до получения одной эквивалентной секции.

Исходные знаки можно объединять в один (рис. 4, в), в результате чего может образоваться, например, система параллельных секций, решение которой приведено на рис. 4, б. Для рис. 4, в последовательно получим:

; . (13)

Другими элементарными преобразованиями являются эквивалентные замены «треугольника» на «звезду» (рис. 4, г) и «звезды» на «треугольник» (рис. 4, д). Обозначим для краткости написания эти замены условно: соответственно ТЗ и ЗТ.

В преобразовании ТЗ (рис. 4, в) получается условная точка Х с группой из трех эквивалентных секций между этой точкой и узловыми точками А, В и С. Точка Х также является и узловой точкой. Качественные характеристики эквивалентных секций определяются по формулам:

; ; , (14)

где - называется периметром «треугольника».

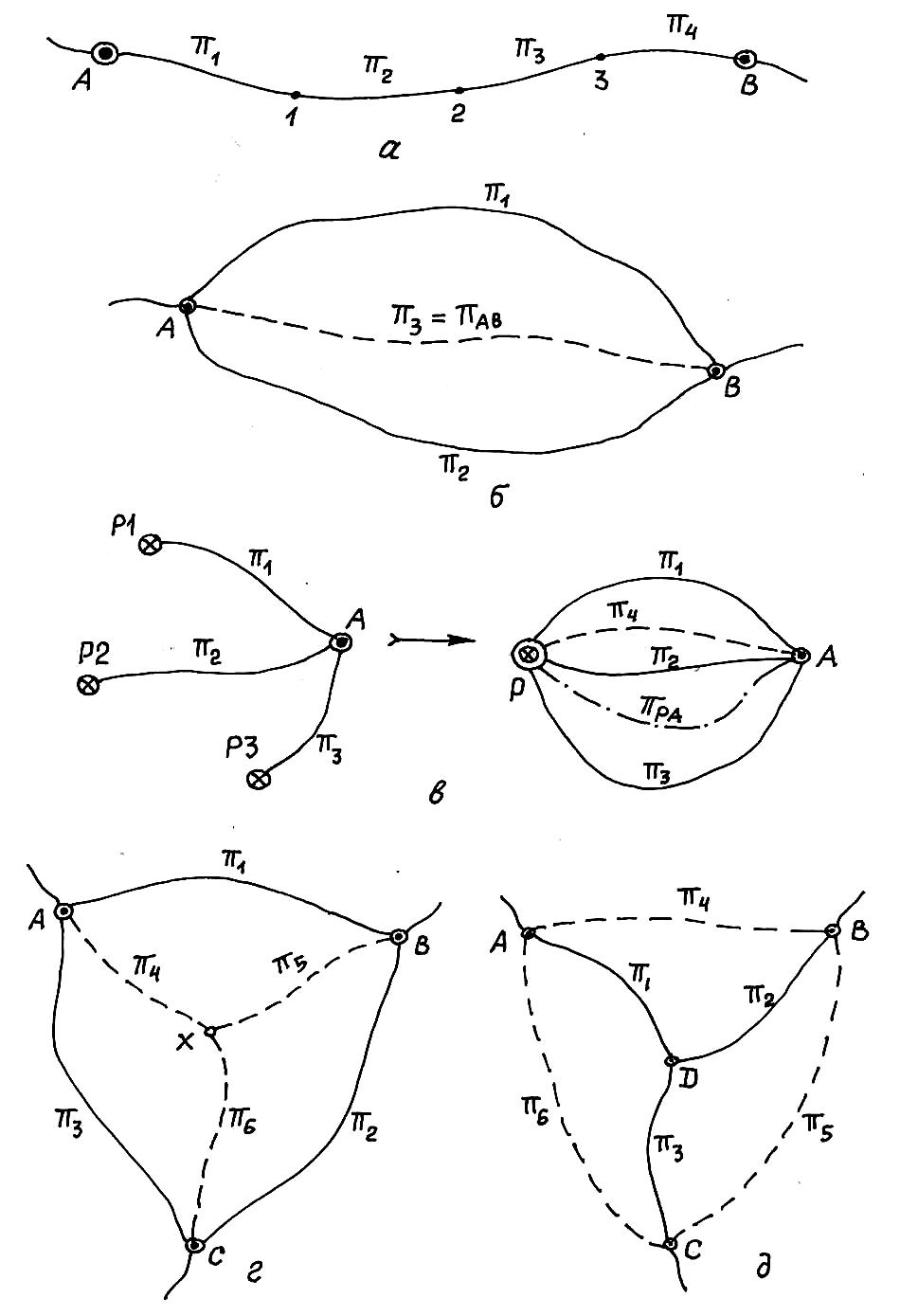
Рис. 4. Простейшие эквивалентные преобразования в нивелирных ходах

В преобразовании ЗТ (рис. 4, г) «исчезает» общая узловая точка D, а новые эквивалентные секции образуются между оставшимися узловыми точками А, В и С. В этом случае

; ; , (15)

где .

3.3. Поиск слабоопределяемой точки системы нивелирных ходов

Исследование системы нивелирных ходов заключается в поиске деформационного знака (знаков), имеющих в эквивалентной схеме, представляющей одну секцию между ним и исходным знаком, максимальное значение качественной характеристики π_Е. Точка Е называется в этом случае слабоопределяемой. Эквивалентная секция Р-Е учитывает комплекс связей при перемещении к слабоопределяемой точке по всем возможным подходам к ней от всех исходных геодезических знаков.

Очевидно, что сразу затруднительно ответить на вопрос, в каком полигоне, в какой секции находится слабоопределяемая точка. Однако в местах, близких к узловым точам, к которым выполнена привязка, слабоопределяемых точек не может быть.

Рассмотрим систему ходов, показанную на рис. 3. Здесь можно полагать, что слабоопределяемая точка находится в полигоне А, как наиболее удаленном от узловых точек 12 и 19, примерно в середине этого полигона.

Выполним последовательно эквивалентные преобразования приближениями от исходных знаков к полигону А.

Предварительно преобразуем полигон В с подходным ходом Р2-19.

Для подходного хода .

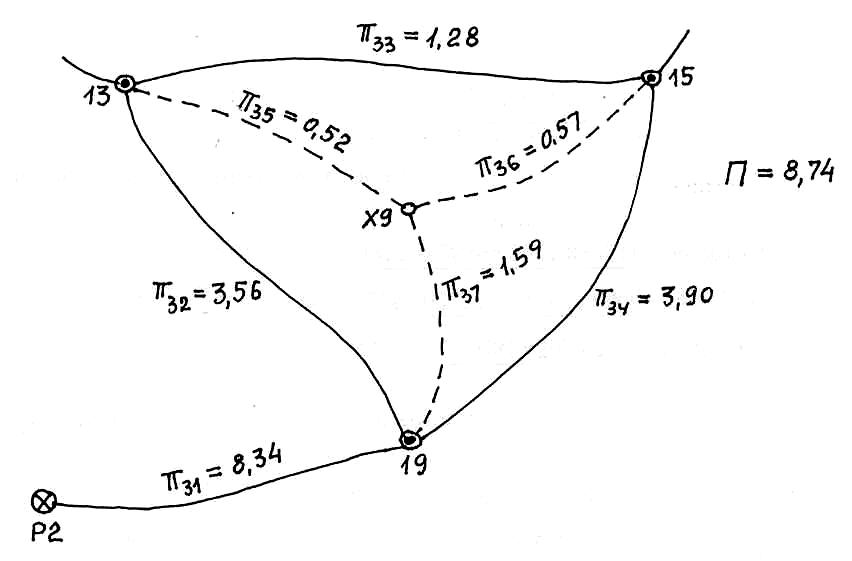
Рис. 5. Преобразование полигона В

Образуем «треугольник» 13-15-19 с секциями (рис. 5):

Для новых вычисленных здесь и в дальнейшем качественных характеристик составим таблицу 3.

Таблица 3

Качественные характеристики преобразованных секций

πi	Значение πi	πi	Значение πi	πi	Значение πi
π31	8,34	π38	9,48	π45	0,22
π32	3,56	π39	9,93	π46	10,48
π33	1,28	π40	5,66	π47	4,47
π34	3,90	π41	2,28	π48	0,97
π35	0,52	π42	0,85	π49	1,07
π36	0,57	π43	0,55	π50	2,82
π37	1,59	π44	1,47	π51

В «треугольник» 13-15-19 введем узловую точку Х9 и выполним преобразование ТЗ (рис. 4, в).

Периметр «треугольника» .

;

;

.

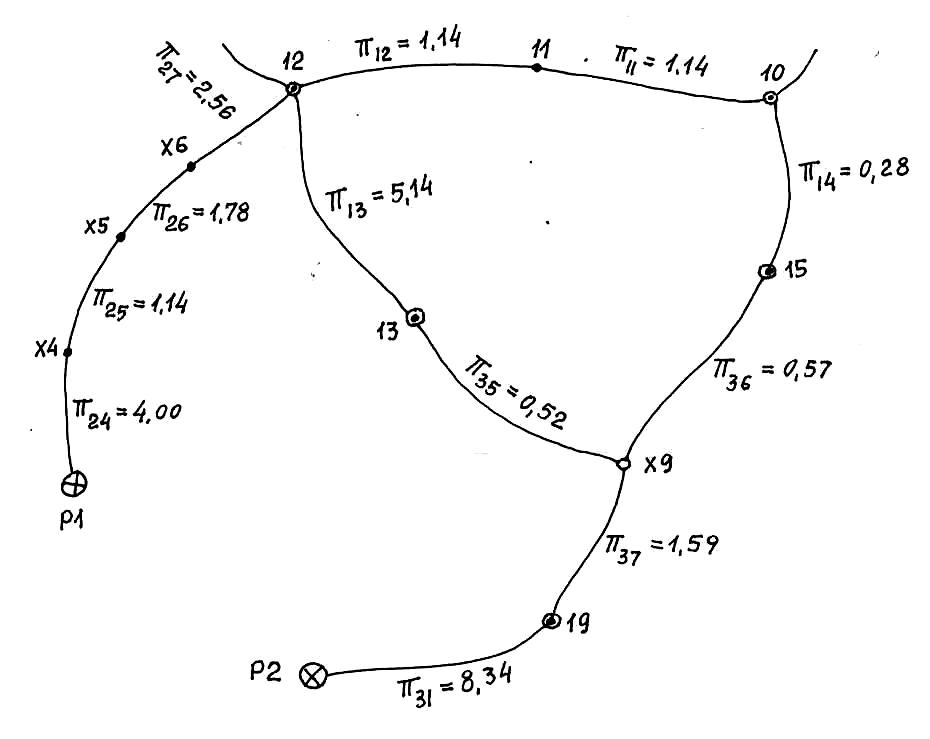
Рис. 6. Группа секций для исследования полигона Б

Следующее преобразование заключается в эквивалентной замене полигона Б. С учетом предыдущего преобразования получим совместную схему (рис. 6). Составим в этой схеме объединенные секции (рис. 7):

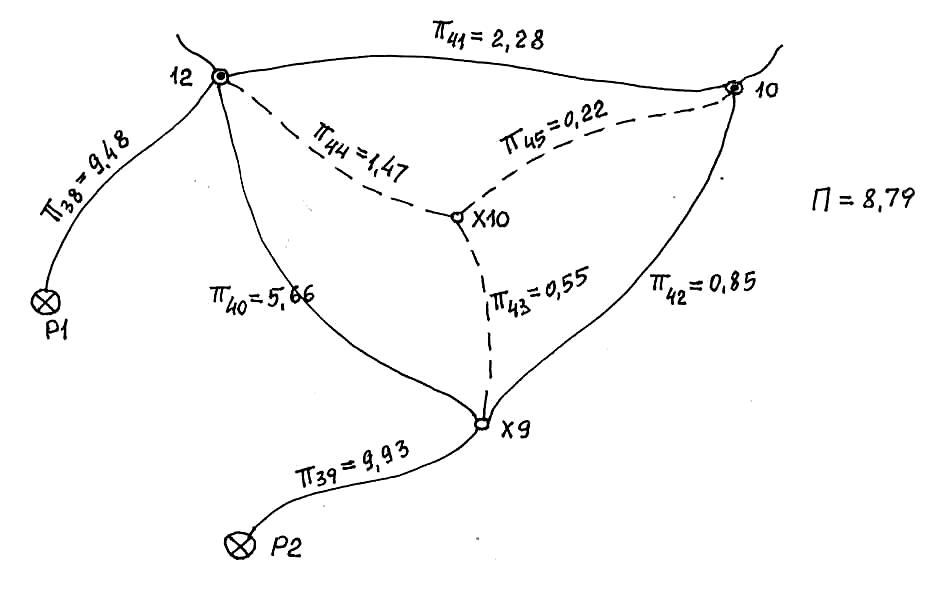
Рис. 7. Полигон Б в виде «треугольника»

;

;

;

;

.

Преобразуем далее «треугольник» 12-10-Х9 в «звезду» с узловой точкой Х10.

Периметр «треугольника» .

;

;

.

Далее целесообразно объединить исходные точки Р1 и Р2 (рис. 8а) в один исходный знак. С учетом схемы рис. 7 .

В результате получим «треугольник» 12-Х10-Р, который заменим «звездой» с узловой точкой Х11 (рис. 8б).

Периметр «треугольника» .

;

;

.

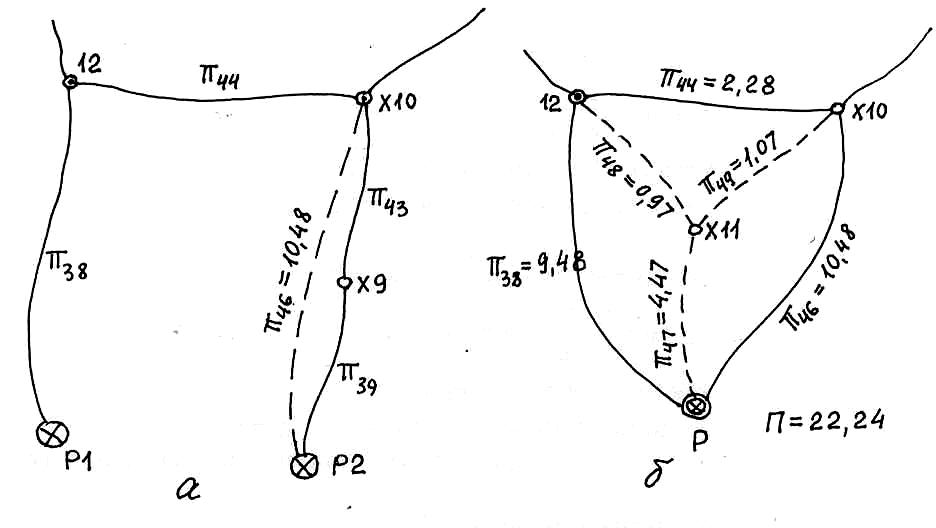
Рис. 8. Объединение исходных геодезических знаков

При сравнении эквивалентной системы нивелирных ходов (рис. 8, б) и общей схемы (рис. 3) видно, что точки 12, Х11 и Х10 оказались включенными в полигон А, исследуемый на наличие слабоопределяемой точки. Эта общая схема представлена на рис. 9.

Периметр исследуемого полигона А в данном случае равен сумме качественных характеристик его секций (без подходного хода Р-Х11):

.

Максимальное значение π эквивалентной полигону секции Х11-Е определяется равенством ветвей (ходов) к точке Е от точки Х11 по левой и правой сторонам, т.е. при

.

Для этого случая, как следует из формулы (12),

.

Найдем слабоопределяемые деформационные знаки, для которых при движении от точки Х11 по левой и правой ветвям будет достигнуто значение . Для этого представим наше движение в виде таблицы (табл. 4).

Таблица 4

Поиск слабоопределяемого деформационного знака

Х11	12	1	2(3)	4	Х1	5	6(7)	8
Левая ветвь	0,97	2,75	3,39	4,03	4,47	5,11	5,55	6,42
Правая ветвь	1,07	1,29	1,93	3,71	4,85	5,72
Х11	Х10	10	Х2	9	8	6(7)

Как видно из таблицы 4, слабоопределяемая точка находится в секции [6(7)-8]. Однако, поскольку точки Е, как таковой, не существует, то установим, какая из двух точек, 6(7) или 8, имеют большее значение π. Сравним для этого произведения и . Из этого заключаем, что слабоопределяемой точкой является двойная точка 6(7).

Рис. 9. Исследование полигона А

Получим для этой точки в полигоне значение π эквивалентной секции (периметр полигона равен 11,27):

.

Вообще говоря, здесь из-за округлений получилось практически то же значение, которое было установлено для максимального эквивалентного хода данного полигона – 2,82.

Общее значение π для точки 6(7) с учетом привязки Р-Х11 равно:

.

3.4. Невязки в полигонах и разомкнутых ходах

Допустимая невязка в превышениях для разомкнутого хода или для полигона при равноточных измерениях определяется по формуле:

, (16)

где n – число станций (секций) в ходе.

При неравноточных измерениях в подкоренное выражение входит сумма качественных характеристик секций, образующих данный полигон или разомкнутый ход:

. (17)

Воспользуемся формулой (17) для анализа некоторых полигонов в нивелирных ходах, представленных в качестве примера (рис. 3):

- для полигона А ( ) при m_h = 0,26 мм f_hДОП = 2,6 мм;

- для полигона Б ( ) при m_h = 0,26 мм f_hДОП = 2,3 мм;

- для разомкнутого хода Р1-12-13-20-19-Р2 ( ) при m_h= 0,26 мм f_hДОП = 4,0 мм.