1) Проверим наличие аномальных наблюдений

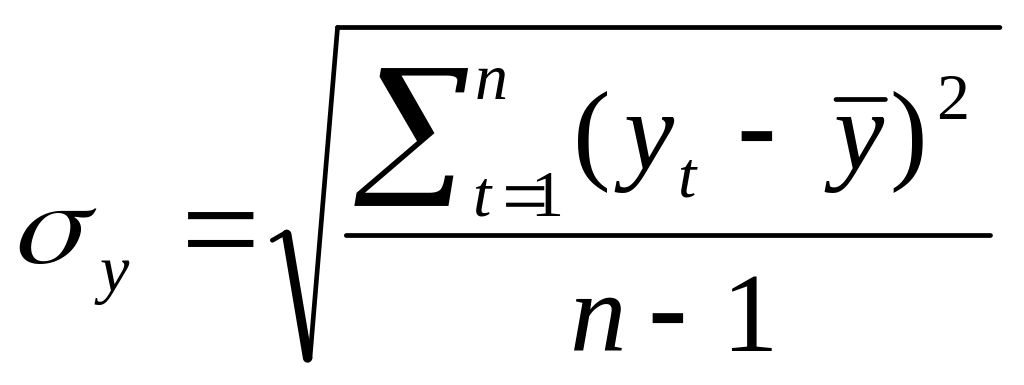= 14,71

Результаты расчетов приведены в таблице 2.1.

Таблица 2.1

t	y	y-yt-1	|y-yt-1|
1	10,8
2	14,8	4	4	0.27
3	21,8	7	7	0.48
4	24,8	3	3	0.20
5	33,8	9	9	0.61
6	41,8	8	8	0.54
7	44,8	3	3	0.20
8	47,8	3	3	0.20
9	49,8	2	2	0.14
	312.7		39	2.65

Сравним расчетное значение с табличным значением ( =1,5). Все расчетные значения меньше , следовательно, аномальных значений во временном ряду нет.

2) Построим линейную модель

Рассчитаем коэффициенты линейной модели с помощью инструмента Регрессия программы Excel. В качестве входного интервала Y берем значения спроса на кредитные ресурсы финансовой компании в качестве входного интервала Х – номера наблюдений.

Результаты приведены в таблице:

Таблица 2.2а

Регрессионная статистика
Множественный R	0,983716989
R-квадрат	0,967699115
Нормированный R-квадрат	0,963084703
Стандартная ошибка	1,782599948
Наблюдения	9

Таблица 2.2б

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	437,4	437,4	209,712329	2E-06
Остаток	7	14,6	2,085714286
Итого	8	452

Таблица 2.2 в

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	8,24	1,04918714	1,111971949	0,30287593
t	5,3	0,18644545	14,48144774	1,7853E-06

Таблица 2.2 г

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
1	11.04	-0.24
2	16.34	-1.54
3	21.64	0.16
4	26.94	-2.14
5	32.24	1.56
6	36.74	4.26
7	42.84	1.96
8	48.14	-0.34
9	53.44	-3.64

Уравнение линейной модели будет иметь вид:

= 8,24+5,3*t

3) Оценим адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения.

Модель является адекватной, если математическое ожидание значений остаточного ряда близко или равно нулю, и если значения остаточного ряда случайны, независимы и подчинены нормальному закону распределения.

а) При проверке независимости (отсутствия автокорреляции) определяется отсутствие в ряду остатков систематической составляющей (с помощью d-критерия Дарбина-Уотсона).

Таблица 2.3

Таблица для вычисления d-критерия

Наблю- дение	Y расчетное	Отклонение E(t)	E(t)- E(t-1)	(E(t)- E(t-1))2	E(t)2
1	11.04	-0.24			0.058
2	16.34	-1.54	-1.3	1.69	2.372
3	21.64	0.16	1.7	2.89	0.026
4	26.94	-2.14	-2.3	5.29	4.580
5	32.24	1.56	3.7	13.69	2.434
6	36.74	4.26	2.7	7.29	18.148
7	42.84	1.96	-2.3	5.29	3.842
8	48.14	-0.34	-2.3	5.29	0.116
9	53.44	-3.64	-3.3	10.89	13.250
СУММА		0,000		52.32	44.82

(Значения остатков взяты из таблицы 2.2 г)

Зададим уровень значимости равной 0,05. По таблицам значений критерия Дарбина-Уотсена для числа n=9 и числа независимых переменных модели k=1 критическое значение d₁=0,82 и d₂=1,32

Так как d попало в интервал от 0.82 до 1.32, то по данному критерию модель адекватна.

б) Проверку случайности уровней ряда остатков проведем на основе критерия поворотных точек.

В случайном ряду чисел должно выполняться строгое неравенство: р  2(N-2)/3-2(16N-29)/90]. Количество поворотных точек равно 4 (Рисунок 2,1.). Правая часть неравенства равна 2,41. Неравенство выполняется (42), следовательно, свойство случайности выполняется. Модель по этому критерию адекватна.

Рис.2.1

в) Соответствие ряда остатков нормальному закону распределения определим при помощи RS-критерия.

RS=E_max –E_min  S_E

E_max – максимальный уровень ряда остатков = 4,26;

E_min – минимальный уровень ряда остатков = - 3,64;

S_E – среднее квадратичное отклонение

S_E = = = 2.37

RS=4,26–(-3,64) 2,37= 3,33

Расчетное значение попадает в интервал (2,7 - 3,7), следовательно, свойство нормальности распределения выполняется. Модель по этому критерию адекватна.