Понятие дельта-функции Дирака и ее использование в теории информации
<общие сведения>
Дельта-функция Дикара позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или приложенной в одной точке.
Например,
плотность единичной точечной массы,
находящейся в точке a евклидова
пространства 
,
записывается с помощью δ-функции
в виде δ(x − a).
Также применима для описания распределений
заряда, массы и т. п. на поверхностях или
линиях.
<общие сведения>
<определение>
δ-функция с областью определения определяется формальным соотношением
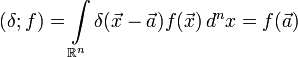
для
любой непрерывной функции 
.
В
частности, для одномерной
дельта-функции (то
есть дельта-функции с областью
определения 
)
.
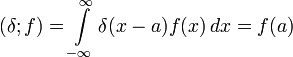Д
ирак
в книге «Принципы квантовой механики»
[5] определил дельта-функцию δ(x)
следующим образом:
.
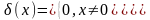Кроме того задается условие:
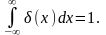
Наглядно можно представить график функции, похожей на δ(x), как показано на рисунке 1
</определение>
<использование>
дельта-функция решает вопрос о производной в точке разрыва (в частности, для разрыва, имеющего вид конечного скачка).
Нахождение производных разрывных функций.
</использование>
<пример>
</пример>
Разновидности модуляции
<определение>
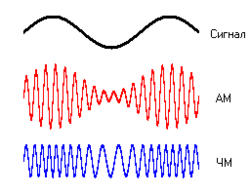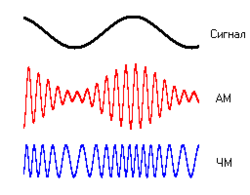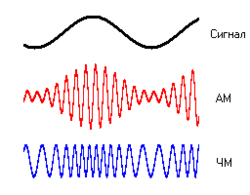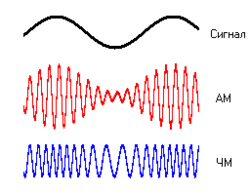
В телекоммуникациях, модуляция – это процесс изменения периодической формы, т.е. сигнала, цель которого – передача сообщения, также как и музыкант может моделировать звук музыкального инструмента изменяя его громкость, длительность и интонацию. Обычно высокочастотный синусоидальный сигнал используется как несущий сигнал. Три ключевых параметра синусоидального сигнала – это амплитуда (громкость), фаза (длительность) и частота (интонация), все из которых могут быть изменены в соответствии с низкочастотным информационным сигналом для получения модулированного сигнала.
</определение>
<ul>
Аналоговая модуляция
Цифровая модуляция
Импульсная модуляция
</ul>
<theory>
Аналоговая модуляция
Амплитудная модуляция (АМ)
Амплитудная модуляция с одной боковой полосой(SSB — однополосная АМ)
Балансная амплитудная модуляция (БАМ) — АМ с подавлением несущей
Квадратурная модуляция (QАМ)
Угловая модуляция
Частотная модуляция (ЧМ)
Линейная частотная модуляция (ЛЧМ)
Фазовая модуляция (ФМ)
Сигнально-кодовая модуляция (СКМ), в англоязычном варианте Signal Code Modulation (SCM)
Сигма-дельта модуляция (∑Δ)
Амплиту́дная модуляция — вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда
Цифровая модуляция
Амплитудная манипуляция (АМн; англ. amplitude shift keying (ASK), а также англ. continuous wave (CW)) — изменение сигнала, при котором скачкообразно меняется амплитуда несущего колебания. АМн можно рассматривать частный случай квадратурной манипуляции (КАМн англ. quadrature amplitude shift keying (QASK)).
Фа́зовая манипуля́ция (ФМн, англ. phase-shift keying (PSK)) — один из видов фазовой модуляции, при которой фаза несущего колебания меняется скачкообразно.
При частотной манипуляции (ЧМн, англ. Frequency Shift Keying (FSK)) значениям «0» и «1» информационной последовательности соответствуют определённые частоты синусоидального сигнала при неизменной амплитуде. Частотная манипуляция весьма помехоустойчива, поскольку помехи телефонного канала искажают в основном амплитуду, а не частоту сигнала. Однако при частотной манипуляции неэкономно расходуется ресурс полосы частот телефонного канала. Поэтому этот вид модуляции применяется в низкоскоростных протоколах, позволяющих осуществлять связь по каналам с низким отношением сигнал/шум.
Частотная манипуляция с минимальным сдвигом (англ. Minimal Shift Keying (MSK)) представляет собой способ модуляции, при котором не происходит скачков фазы и изменение частоты происходит в моменты пересечения несущей нулевого уровня. MSK уникальна потому что значение частот соответствующих логическим «0» и «1» отличаются на величину равную половине скорости передачи данных. Другими словами, индекс модуляции равен 0,5: