<!DOCTYPE html55> (W3C valid) by NX
Использование теоремы Котельникова в теории информации
<отступление>
Теория информации (математическая теория связи) — раздел прикладной математики, определяющий понятие информации
<пояснение>
[Информация (от лат. informatio — осведомление, разъяснение, изложение, от лат. informare — придавать форму) — в широком смысле абстрактное понятие, имеющее множество значений, в зависимости от контекста. В узком смысле этого слова — сведения (сообщения) независимо от формы их представления],
</пояснение>
её свойства и устанавливающий предельные соотношения для систем передачи данных. Как и любая математическая теория, оперирует с математическими моделями, а не с реальными физическими объектами (источниками и каналами связи). Использует, главным образом, математический аппарат теории вероятностей и математической статистики.
Основные разделы теории информации — кодирование источника (сжимающее кодирование) и канальное (помехоустойчивое) кодирование. Теория информации тесно связана с криптографией и другими смежными дисциплинами.
</отступление>
<Теорема>
Теоре́ма
Коте́льникова (в
англоязычной литературе — теорема
Найквиста — Шеннона или
теорема отсчётов) гласит, что,
если аналоговый
сигнал 
имеет
ограниченный спектр,
то он может быть восстановлен однозначно
и без потерь по своим дискретным отсчётам,
взятым с частотой более удвоенной
максимальной частоты спектра 
:
Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и, обычно, имеют во временной характеристике разрывы. Соответственно, их спектр бесконечен. В таком случае полное восстановление сигнала невозможно и из теоремы Котельникова вытекают 2 следствия:
Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой
,
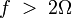где
—
максимальная частота, которой ограничен
спектр реального сигнала.
Если максимальная частота в сигнале превышает половину частоты дискретизации, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.
Говоря шире, теорема Котельникова утверждает, что непрерывный сигнал можно представить в виде интерполяционного ряда
где 
—
функция sinc.
Интервал дискретизации удовлетворяет
ограничениям 
Мгновенные
значения данного ряда есть дискретные
отсчёты сигнала 
.
</Теорема>
<Использование теоремы>
Кратко:
используется при кодирование \ декодировании сигналов из аналогового в цифровой и обратно. Используется как основа таких устройств как (АЦП, англ. Analog-to-digital converter, ADC). для интерполяции временого ряда
Не Кратко и заумно:
Проблемы дискретизации и интерполяции сигналов имеют большое значение как в теории
сигналов с финитным спектром, так и случайных процессов. При выборе шага дискретизации
возникают задачи оценки погрешности замены непрерывных процессов дискретными, а также
оптимизации характеристик интерполирующих фильтров по критерию минимума
среднеквадратической ошибки интерполяции . Использование обобщенной теоремы Котельникова позволяет эффективно решать эти задачи.
На первом этапе
приводится общая теория оценки погрешности восстановления непрерывных сигналов по
дискретным отсчетам, а на втором рассматривается метод интерполяции случайных процессов АФ
и их преобразованиями Фурье
<file> Подробнее смотри в Использование теоремы Котельникова.pdf </file>
</Использование теоремы>