РЯДЫ

Символьное вычисление конечных сумм и сумм сходящихся рядов в Mathcad выполняется с помощью панели инструментов Матанализ.

Для того чтобы вычислить сумму, щелкните по свободному месту в рабочем документе, затем — по кнопке в панели Матанализ, введите с клавиатуры в помеченных позициях выражение для функции, имя индекса суммирования, его первое и последнее значения (для рядов введите в качестве последнего значения символ бесконечности, щелкнув по кнопке с символом в той же панели), заключите все выражение в выделяющую рамку и щелкните по строке Символические в пункте Расчеты в меню Символы (или нажмите на клавиатуре комбинацию клавиш <Shift>+ <F9>). Для того чтобы получить вычисленное значение в десятичном формате, выделите его, щелкните в том же меню по строке С плавающей запятой и введите в окне диалога требуемое число десятичных знаков. Можно сразу получить значение суммы в десятичном формате, если щелкнуть вместо Символические по строке С плавающей запятой.

Числовые ряды Основные понятия. Ряды с неотрицательными членами

Рассмотрим произвольную числовую последовательность {u_n}. Фор­мально составленное выражение

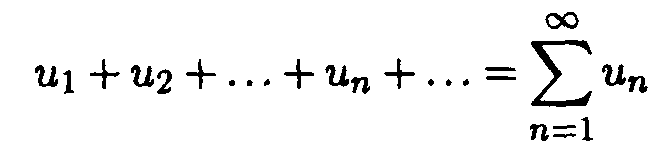
называют числовым рядом или просто рядом. Члены последовательно­сти {u_n} называют членами ряда. Сумма первых п членов ряда

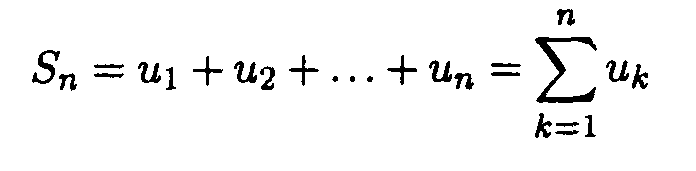
называется п-й частичной суммой ряда.

Ряд

называется сходящимся, если существует и конечен предел последовательности {S_n} частичных сумм этого ряда. При этом предел последовательности частичных сумм называется суммой ряда. Обозначаем

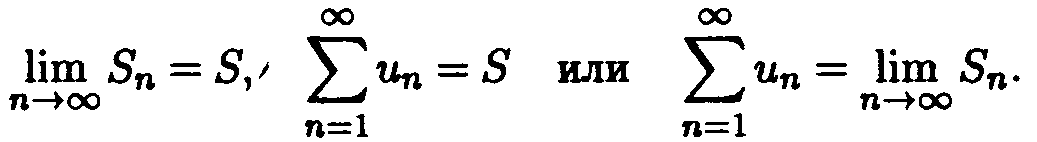
Если предел последовательности частичных сумм не существует или бесконечен, то ряд расходится. Справедливо следующее утверждение. Для того чтобы ряд сходился, необходимо, чтобы последовательность его членов {и_п} стремилась к нулю при п . Другими словами, если ряд сходится, то его члены стремятся к ну­лю на бесконечности. Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом расходится.

Наиболее часто встречающиеся ряды — расходящийся ряд , который называется гармоническим рядом, и сходящийся ряд, называемого рядом Лейбница. Другие часто встречающиеся ряды — обобщенный гармонический ряд , который сходится при  > 1 и расходится при   1 (при  = 1 получаем гармонический ряд), и ряд типа прогрессии , который сходится при |q| < 1 и расходится при |q|  1.

Исследовать на сходимость числовые ряды с неотрицатель­ными членами можно, используя теоремы сравнения и признаки сходимости.

1. Рассмотрим два числовых ряда с неотрицательными членами и a_n  0, b_n  0. Если при всех п, начиная с некоторого, справедливо неравенство a_n  b_n, то из сходимости ряда следует сходимость ряда ; и наоборот, из расходимости ряда следует расходимость ряда

2. Рассмотрим два числовых ряда с неотрицательными членами и , a_n  0, b_п > 0. Если , c  0, то ряды и сходятся или расходятся одновременно.

При использовании теорем сравнения исследуемый ряд чаще всего сравнивают с простейшими рядами — с обобщенным гармоническим или с рядом типа прогрессии.

Признак сходимости Даламбера. Для ряда с положительными членами , a_п > 0, вычислим предел Если d < 1, то ряд сходится, если d > 1 — расходится. При d = 1 вопрос о сходимости ряда остается открытым: ряд может оказаться как сходящимся, так и расходящимся.

Признак сходимости Коши. Для ряда с положительными членами , a_п > 0, вычислим предел . Если с < 1, то ряд сходится, если с > 1, — расходится. При с = 1 вопрос о сходимости ряда остается открытым: ряд может оказаться как сходящимся, так и расходящимся.

ЗАДАНИЕ 24

Исследуйте на сходимость ряды , , , и . Если удается, вычислите сумму ряда.

Порядок выполнения задания

1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали.

2. Определите члены исследуемых рядов как функции переменной п.

3. Примените к ряду первую теорему сравнения, сравнивая его с обобщенным гармоническим рядом или с рядом типа прогрессии.

4. Примените к ряду вторую теорему сравнения, сравнивая его с обобщенным гармоническим рядом или с рядом типа прогрессии

5. Сформулируйте и запишите в рабочем документе вывод.

6. Примените к ряду признак Даламбера

7. Сформулируйте и запишите в рабочем документе вывод.

8. Примените к ряду признак Коши.

9. Сформулируйте и запишите в рабочем документе вывод.