3.7.2.Формула Байеса.

Базируется на формуле полной вероятности и теореме умножения вероятностей.

Пусть до проведения некоторого опыта об его условиях n можно сделать n исключающих друг друга предположений (гипотез), образующих полную группу:

Вероятности гипотез до опыта (априорные вероятности) известны:

Опыт произведен, и произошло некоторое событие А. Требуется определить вероятности гипотез с учетом того, что произошло событие А, т.е.определить апостериорные вероятности:

Вероятность того, что событие А произошло совместно с Нi, на основании теоремы умножения вероятностей равна

Отбросим левую часть равенства и выразим

Раскроем p(A) по формуле полной вероятности (3.1) и получим формулу Байеса

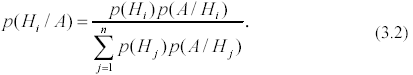
Формула Байеса позволяет пересчитать априорные вероятности гипотез с учетом того, что опыт завершился событием А.

3.7.3.Формула Бернулли.

Теорема о повторении опытов

Пусть проводятся n независимых одинаковых опытов, в каждом из которых событие А появляется с вероятностью р.

Вероятность P(n, k) того, что событие А произойдет ровно в k опытах, равна (формула Бернулли):

где q = 1 – р – вероятность того, что А не появится в одном опыте.

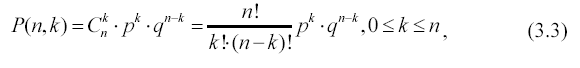
Свойства формулы Бернулли:

1. Правая часть формулы (3.3) представляет собой общий член разложения бинома Ньютона:

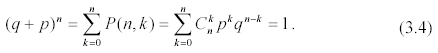
2. Рекуррентная формула P(n, k)имеет вид

3. Число к0, которому соответствует максимальная вероятность P (n, k0) , называется наивероятнейшим числом появления события А и определяется неравенствами

Вычисление вероятностей P (n ,k ) при больших значениях n по формуле Бернулли проблематично. Поэтому вычисление соответствующих вероятностей проводится с помощью следующих приближенных формул.

Если количество испытаний велико а вероятность события мала

то используется формула Пуассона:

(3.7)

Если количество испытаний n велико, вероятности p и q не малы, так что выполняются следующие условия:

то применяются приближенные формулы Муавра–Лапласа:

– локальная

(3.8)

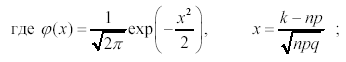
– интегральная

(3.9)

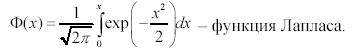
При использовании таблиц следует помнить, что . является четной а функция Лапласа – нечетной

3.8.Дискретные и непрерывные случайные величины.

Под случайной величиной (СВ) понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение, причем заранее, до опыта, неизвестно, какое именно.

Случайные величины будем обозначать большими буквами: их значения – соответствующими малыми буквами: x, y, z, а

Примеры случайных величин:

1. Опыт – бросок одной игральной кости; случайные величины Х – число выпавших очков;

2. Опыт – работа ЭВМ до первого отказа; случайные величины X – время наработки на отказ;

В зависимости от вида множества случайные величины могут быть дискретными и непрерывными.

Случайная величина (СВ) Х называется дискретной, если множество – счетное, т.е. его элементы можно расположить в определенном порядке и пронумеровать.

Случайная величина Х называется непрерывной (недискретной), если множество – несчетное.

Законом распределения случайной величины Х называется любая функция (правило, таблица и т.п.), устанавливающая соответствие между значениями случайной величины и вероятностями их наступления и, позволяющая находить вероятности всевозможных

связанных со случайной величиной.