Теорема сложения для n случайных событий.
Вероятность суммы n событий A1, ..., An равна
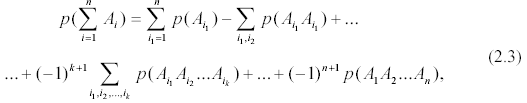
где число слагаемых в
k-й
сумме равно
, т.е. перебираются
все возможные сочетания из k
слагаемых.
Доказательство.
Используем метод математической индукции. Однако для экономии времени и места докажем переход от m слагаемых к m+1 для
случая m = 2.
Докажем, что
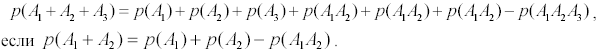
Обозначим
что и требовалось доказать.
На практике, с учетом
того что
,
вероятность суммы n
событий (если n
> 2) удобнее вычислять по формуле
Теорема умножения вероятностей для двух событий.
Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого:
Доказательство.
Докажем (2.7) для схемы случаев.
Пусть в опыте возможны n несовместимых и равновозможных исходов.
Событию А соответствует m исходов, событию B – k исходов.
В l исходах события А и В происходят одновременно.
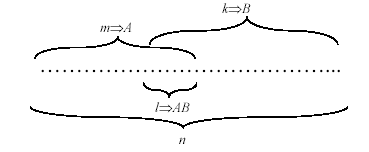
Очевидно,что
Вычислим условную вероятность p(В /А), т.е. вероятность события В в предположении, что А произошло.
Если известно, что событие А произошло, то из ранее возможных n случаев остаются возможными только те m, которые благоприятствовали событию А.
Из них l
благоприятны событию
.
Аналогично вычислим условную вероятность p(A/B), т.е. вероятность события A в предположении, что B произошло:
Подставим найденные найденные вероятности в (2.7)
что
и требовалось доказать. Очевидно, что
безразлично, какое из событий считать
первым, а какое вторым.
Теорема умножения вероятностей для n событий.
Вероятность произведения n событий А1 +Аn равна
где
- вероятность появления события Ak,
при условии что события
в
данном опыте произошли.
Доказательство.
Используем метод математической индукции.
Однако для экономии времени и места докажем переход от m сомножителей к m+1 для случая m = 2. Докажем, что
если
что и требовалось доказать.
Если события А1 +Аn независимы, то вероятность произведения равна произведению вероятностей этих событий:
а вероятность появления хотя бы одного события А1, А2, ...,Аn равна (см. (2. 4))
3.6. Решение типовых задач.
Пример 1.
Найти вероятность выпадения герба (событие А) при бросании монеты.
Решение.
Общее число равновозможных случаев n = 2 — орел и решка.
Число благоприятствующих случаев (появление орла) равно m = 1.
Тогда вероятность выпадения герба равна: Р(А)=1/2.
Пример 2.
Найти вероятность выпадения грани с цифрой 3 (три очка) (событие А) при однократном бросании шестигранной игральной кости.
Решение.
Число п=6 (по числу граней кубика); та=1 (выпадение цифры 3).
Вероятность появления цифры 3 равна: Р(А)=1/6
Пример 3.
Найти вероятность наступления события А , которое заключается в выпадении не менее 3 очков при однократном бросании игральной кости.
Решение.
Как и в предыдущем примере, общее число равновозможных случаев n = 6;
число случаев благоприятствующих ma=4, поскольку интересующему нас событию (выпадение не менее 3 очков) удовлетворяют случаи выпадения 3, 4, 5 и 6 очков. Следовательно, вероятность выпадения не менее 3 очков равна:
Р(А) = 4/6 = 2/3
Пример 4.
В урне находится 10 шаров, из них 3 красных и 7 синих. Найти вероятность того, что взятые наугад два шара оба окажутся красными.
Решение.
В данном примере общее число равновозможных случаев равно числу сочетаний из всего числа шаров по два n = C210 поскольку любые два шара могут быть вынуты с равными шансами. Число благоприятствующих случаев равно числу сочетаний из числа красных шаров по два ma = C23 , ибо только такие сочетания удовлетворяют требованию выбора двух красных шаров.
Следовательно,
P(A) = C23 / C210 =3 / 45 = 1 / 15
Пример 4.
В ящике m белых и n черных шаров. Шары тщательно перемешаны. Наудачу вынимают сразу два шара.
Какова вероятность того, что оба вынутые шара белые?
Решение.
#G0Вариант 1.
1.Пронумеруем шары (от 1 до m + n).
2. Так как порядок появления
шаров неважен (он не указан), то общее
число возможных комбинаций равно
.
3. Пусть А - событие, когда
оба шара белые. Тогшда число таких
комбинаций равно
.
4. По формуле определения
классической вероятности находим:
.
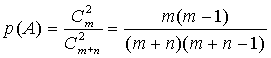Вариант 2.
1. События - оба шара белые и 1ый и 2ой шары белые - совпадают. Достаточно вычислить вероятность события, которое представляет собой произведение событий: А = {вынутый первый шар является белым}, B = { вынутый второй шар является белым}
2.
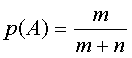и , поскольку, если событие А произошло,
то в ящике осталось n+m-1 шаров, среди
которых m-1 белых, и вероятность снова
вынуть белый шар будет равна:
.
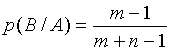3. Воспользуемся формулой
произведения вероятностей:
.
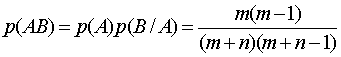Пример 5.
В партии из10 деталей 7 стандартных.
Найти вероятность того, что среди 6ти взятых наугад деталей - 4 стандартных.
Решение.
1. Общее число возможных элементарных исходов испытания(опыта)равно числу способов, которыми можно извлечь 6 деталей из 10,т.е.
2. Общее число исходов,
благоприятствующих интересующему нас
событию А равно:
.
3.
Искомая вероятность
.
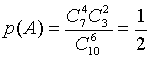Пример 6.
Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово "кукла"?
Решение.
Используем
классическое определение вероятности:
P=m/n, где n - число всех возможных элементарных
исходов, m - число элементарных исходов,
благоприятствующих осуществлению
события, заключающегося в том, что
ребенок соберет из кубиков слово «Кукла».
Число различных перестановок из
букв (элементов) множества { А, К, К, Л,
У}равно
,
из них только одна соответствует слову
"кукла" (m=1), поэтому вероятность
того, что ребенок соберет из кубиков
слово "кукла" равна P=1/60.
Ответ:
1/60.
Пример 7.
Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
Решение.
Пусть
-
вероятность попадания в цель при одном
выстреле. Введем событие X = {при четырех
выстрелах есть хотя бы одно попадание}
и противоположное ему событие
=
{при четырех выстрелах нет ни одного
попадания}.
Вероятность события
равна
,
тогда вероятность события Х равна
.
По условию эта вероятность равна 0,9984,
откуда получаем уравнение относительно
Ответ:
0,8.
Пример 8.
.
Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе - 0,9, в третье - 0,8. Найти вероятность следующих событий: а) только одно отделение получит газеты вовремя; б) хотя бы одно отделение получит газеты с опозданием.
Решение.
Введем
события
А1 = (газеты доставлены
своевременно в первое отделение),
А2
= (газеты доставлены своевременно во
второе отделение),
А3 = (газеты
доставлены своевременно в третье
отделение),
по условию P(A1)=0,95;
P(A2) = 0,9;
P(A3)=0,8.
Найдем вероятность события Х =
(только одно отделение получит газеты
вовремя). Событие Х произойдет, если
или газеты доставлены своевременно
в 1 отделение, и доставлены не вовремя
во 2 и 3,
или газеты доставлены
своевременно в 2 отделение, и доставлены
не вовремя во 1 и 3,
или газеты доставлены
своевременно в 3 отделение, и доставлены
не вовремя во 2 и 1.
Таким образом,
Так
как события А1, А2, А3 - независимые, по
теоремам сложения и умножения получаем
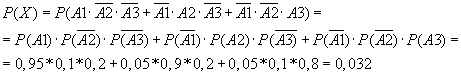Найдем
вероятность события У=(хотя бы одно
отделение получит газеты с опозданием).
Введем противоположное событие
=(все
отделения получат газеты вовремя).
Вероятность этого события
Тогда
вероятность события У:
Ответ:
0,032; 0,316.
3.7.Формулы полной вероятности, Байеса и Бернулли.
Следствием обеих теорем вероятности: теоремы сложения и теоремы умножения – является формула полной вероятности.
3.7.1.Формула полной вероятности.
Пусть проводится опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез), образующих полную группу:
Каждая из гипотез осуществляется случайным образом и представляет собой случайное событие. Вероятности гипотез известны и равны:
Рассмотрим некоторое событие А, которое может появиться только
вместе с одной из гипотез. Известны условные вероятности события А для каждой из гипотез:
Требуется определить полную (безусловную) p(А) вероятность события А.
Представим событие А как сумму из n несовместимых вариантов:
На основании второй аксиомы
С учетом теоремы умножения
вероятностей
