Алгоритмы и модели алгоритмов

Причины развития теории алгоритмов.

1. Появление вычислительной техники

2. Помимо чисел имеется мн-во других элементов

Теория алгоритмов родилась в 30-е годы 20 века.

Различные варианты теории:

1. Алгоритмы представлялись, как рекурсивные функции

2. Модели в виде некоторого устройства (напр. Машина Тьюринга, Схема Ляпунова)

3. Модели алгоритмов, как некие преобразования символьных строк (алгоритмы Маркова)

Эти модели алгоритмов оказались эквивалентны между собой.

В основе всех этих моделей лежит понятие вычислимой функции, для вычисления которой существует алгоритм.

Теория алгоритмов используется, чтобы понять, существует ли конкретный алгоритм, и чтобы оценить каждый алгоритм по времени выполнения, занимаемой памяти, и сравнивать разные алгоритмы между собой.

Алгоритм – это детерминированная последовательность однозначно определенных шагов, которые вырабатывают определенный результат.

Свойства алгоритма.

1. Алгоритм всегда имеет дело с обработкой данных, имеет входы и выходы.

2. Состоит из элементарных, четко определенных шагов. (Эффективность)

3. Всегда определен каждый следующий шаг, либо работа алгоритма кончается. (Детерминированность)

4. Останавливается после конечного числа шагов (результативность)

5. Массовость

Машина Тьюринга

(см лекцию из прошлого семестра)

УУ

M = (A,Q, d, q0)

А – мн-во символов на ленте

Q – конечное мн-во состояний машины

d- функция переходов

q0 – конечное состояние.

D: A * Q -> A * Q * {R, L, S}

(Обозревает символ из мн-ва А, головка в состоянии Q. Символ может остаться прежним или изменяется. Головка переходит или нет. (R- right, L – left, S – stay)

Конфигурация машины Тьюринга

K =a1 q a2 a2

УУ

a1

K1  K2  …. Kn

Вычисление на машине Тьюринга – это последовательность конфигураций

Функция вычислима по тьюрингу, если существует машина тьюринга, которая ее правильно вычисляет.

W = f(u), если q1u => q0w (u -> w)

Функция не определена, если машина Т будет бесконечно работать

Лента может быть как бесконечной, так и ограниченной в обе стороны ( вз. одн. Соотв. Между лентами)

В отличие от компьютера она не универсальна. у нее неограниченная память. Команды выполняет человек.

Лекция 8

Опр: Машина Тьюринга U назыв. Универсальной машиной Тьюринга, если для любой машины тьюринга системы команд Et универсальная машина Тьюринга U(Et, a) тождественна исходной машине Тьюринга

Исходные команды данные

Преимущество – на ленте хранятся не только данные, но и команды.

Доказано, что существует универсальная машины Тьюринга, в которой всего 2 состояния

Доказано, что сущ. Универсальная машина Тьюринга, где А = 2 (алфавит всего из 2 символов – бинарный код)

Но не существует у.м.т, где 2 состоянияи и 2 символа.

Для того, чтобы выполнить любую команду обычной машины Тьюринга, имеется целая последовательность универсальных машин Тьюринга.

Тезис Тьюринга

Любой алгоритм может быть реализован на машине Тьюринга

Схема Ляпунова

Аi – линейный оператор.

Ai (i=0, m) - цикл

P A1…… A2 – условие

Для каждого оператора определено описание.

Алгоритмы маркова

Алгоритмы задаются в виде орграфов (граф-схемы)

Есть 2 типа вершин.

1 – распознаватель вхождения (рв) (проверяет, принадлежит ли строка s1 некой другой строке s2)

2 – операторы подстановки. Заменяют некую строку s3 строкой s4 (s3  s4)

ВХОД | | | PB1  ОП1 | | | PB2  ОП2 | | .. Выход

Выгнутая стрелка – для нормальных алгоритмов. Возвращ. Всего либо в первый, либо в конец

Если через некоторое число шагов мы попадаем, то говорят, что алгоритм применим к исходным данным. Иначе алгоритм не применим.

Рекурсивные функции

Функция называется вычислимой, если существует алгоритм, который вычисляет значение этой функции.

1. О(х) == 0

2. S(x) = x+1

3. { Iⁿ_m (x1, x2, …. ,xn) = xm, m<=n) – семейство функций

Функция называется примитивно рекурсивной (прф), если она может быть построена из этих трех функций при помощи конечного числа операторов, суперпозиции и примитивной рекурсии.

S_n^{m (}h, g1….gm)=h(g1(x1,x2….xn), g2(x1….x2)….gm(x1….xn))

Подстановка вместо переменной значение функции другой функциии.

Оператор примитивной рекурсии

R_n(g,h)

F(x1,….xn+1)

G – n

H – n+2

При n+1 аргументе = 0

F(x1,…..xn, 0) = g(x1,…xn)

По аналогии с мат. Индукцией

F(x1,x2…..xn, y+1) = h ( x1,…xn, y, f(x1,x2…..xn,y) )

Лекция 9

Операторы суммирования и произведения – примитивно-рекурсивные операторы (ПРО)

Ограниченный оператор минимизации

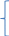F(x1,…xn,z) = μ y P (x1,…xn,y) = min(y<=z : P(x1,..xn,y), если у сущестувет

(y<=z) z, если нет

Мы ищем самый маленький у, при котором предикат выполняется. Если находится, то ставим его в значение функции

Ограниченный он потому, что проверка происходит только до заданного значения z. А все переменные – целые положительные.

Неограниченный оператор минимизации. Не имеет ограничения (z)

F(x1,…xn) = μ y P (x1,…xn,y) = min(y<=z : P(x1,..xn,y), если у сущестувет

(y<=z) не определено

Опр.

Функция называется частично-рекурсивной, если она получена из примитивно-рекурсивной при помощи оператора минимизации (Неограниченного).

Опр.

Обще-рекурсивная функция – это частично-рекурсивная функция, которая всюду определена.

Невычислимые функции

Тотальные ф-ии

ЧРФ

ОРФ

ПРФ

Тотальные фунции – всюду определенные, но не всегда вычислимые функции.

Тезис Чёрча:

Всякая вычислимая функции является частично-рекурсивной

Теорема Чёрча-Тьюринга:

Функция вычислима на машине Тьюринга  она частично рекурсивна

Проблема разрешимости

Надо распространить вычислимые функции на любые функции (тригоном., комплекс, вещественные, символьные и т.п.)

Применяется операция Гёделизация

А* - мн-во слов из этих символов

Пусть А – мн-во символов

Функция g: A* - N Сопоставляет каждому слову некое число.

Проблема называется алгоритмически неразрешимой, если не существует алгоритма (универсального, по св-ву массовости), который ее решает.

Алгоритмически неразрешимая проблема – проблема самоприменимости. (напр. Алгоритм сам определяет, зацикливается он или нет)

Лекция 10

F(x,y) = [ sqrt(x) ] = y?

M_y<=zP(x,y)

P(x,y) = (y+1)² > x

Большинство проблем алгоритмически неразрешимы.

Множество М называется разрешимым, если существует некий алгоритм А_М, который для любого элемента А определяет, принадлежит этот элемент множеству М или нет.

Теорема Райса

Любое нетривиальное свойство вычислимой функции не является алгоритмически разрешимым.

Пусть С – класс функций, облад. Неким нетривиальным свойством. Есть функции, которые этим св-вом не обладают.

Не существует алгоритма, который бы по номеру х функции Fx определил бы, принадлежит ли F классу C, или нет. Или мн-во номеров функции, таких, что эта функция принадлежит классу С. Значит, что это алгоритмически не разрешимо.

Сложность алгоритмов

Асимптотики

Ассимптотики - Технология оценки, скорости роста функции в зависимости от длины вектора данных

F(n) – отражает время работы алгоритма от параметра сложности n

F(n) может быть очень сложным выражением, что не удобно для практического использования.

Задача: придумать некую функцию g(n), которая как-то оценивала эту функцию f.

1. F(n) = o(g(n)) (о- малое. Lim |f/g| = 0) ninf

2. F(n) = O(g(n)) (О-большое. Lim |f/g| = const)

3. F(n) = θ (g(n)) (ограничение с 2 сторон. с1g(n)<=f(n)<=c2g(n) )

Сложность решения задачи – это сложность самого простого алгоритма, решающего эту задачу.

Оценка бывает в

1. Лучшем

2. Худшем

3. Среднем

Существует алгоритмы со сложнотью θ, и не существует алгоритмов с меньшей временной сложностью.

Пространственная сложность – количество памяти, требуемое для решения задачи. Пространственная сложность обычно растет гораздо медленнее, чем временная.