
- •Chapter I. Event and probability
- •1.Events. Operations above events.
- •Venn chart
- •2. Elements of combinatorics.
- •3. Classical definition of probability.
- •4. Geometric definition of probability
- •Chapter II. Basic formulas
- •5. Conditional probability
- •6. Formula of total probability. Bayes’ formulas
- •Chapter III. Bernoulli scheme
- •7. Bernoulli’ formula
- •8. The most probable number of successes in n tests of Bernoulli
- •9. Approximated Poisson formula. Moivre-Laplace theorems
- •Chapter IV. Random variables
- •10. Definition of random variable. Function of distribution
- •11. Finite random variables
- •12. Continuous random variables
- •13. Examples of continuous random variables.
11. Finite random variables
Definition 11.1 A random
value
is called finite if the number of it’s values is finite. If these
values are:
![]() and
and
![]() ,
then can consider the table
,
then can consider the table
|
|
|
… |
|
|
|
|
… |
|
This table
we call the series of distribution of the random variable
.
![]() .
The set
.
The set
![]() we call the domain of the random variable
.
we call the domain of the random variable
.
If we have a
series of distribution we can construct the function of distribution.
If all
![]() are different and
are different and
![]() ,
then
,
then
![]()
Definition
11.2 Two
random variables
with the domain
![]() and
and
![]() with the domain
with the domain
![]() are independent if for any
are independent if for any
![]() and for any
and for any
![]()
![]() .
.
Operations with random variables
Let random variables and are determined by the following series of distribution:
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
Definition
11.3 If
c
is
a constant, then the random variable
![]() is determined as follows:
is determined as follows:
|
|
|
… |
|
|
|
|
… |
|
Definition 11.4 The
random variable
![]() is called the
is called the
![]() degree of
and is determined by the following way:
degree of
and is determined by the following way:
|
|
|
… |
|
|
|
|
… |
|
Definition
11.5 The
random variable
![]() is the sum of
and
.
The sum is determined by the following way.
is the sum of
and
.
The sum is determined by the following way.
Domain:
![]() .
.
Corresponding
probabilities are:
![]() .
.
Definition
11.6 The
random variable
![]() is the difference between
and
.
The difference is determined by the following way.
is the difference between
and
.
The difference is determined by the following way.
Domain:
![]() .
.
Corresponding probabilities are: .
Definition
11.7 The
random variable
![]() is the product of
and
.
The product is determined by the following way.
is the product of
and
.
The product is determined by the following way.
Domain:
![]() .
.
Corresponding probabilities are: .
Mathematical expectation of random variable
Let be a random variable with the series of distribution
|
|
|
… |
|
|
|
|
… |
|
Definition 11.8 Mathematical expectation of is the number
![]() .
.
Properties
of
![]()
If c is a constant, then
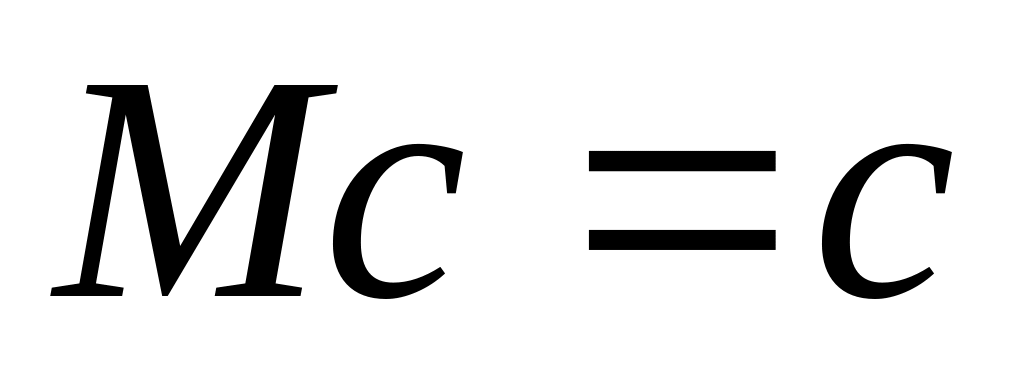 .
.If
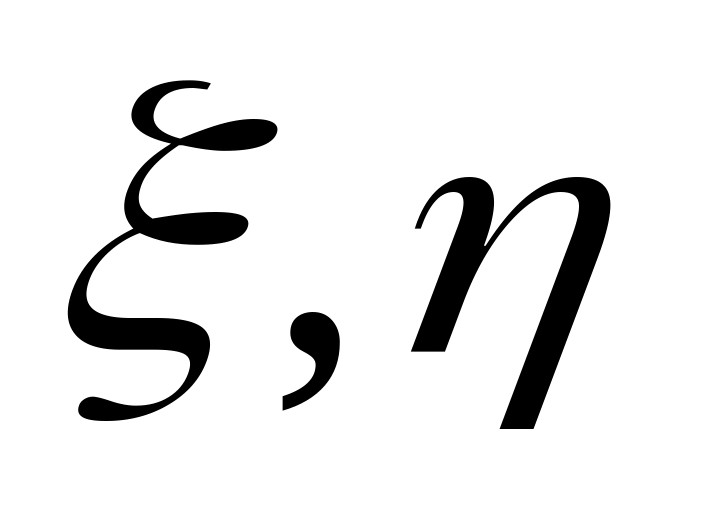 are random variables a,
b are
constants, then
are random variables a,
b are
constants, then
![]() .
.
If random variables are independent, then
![]() .
.
If
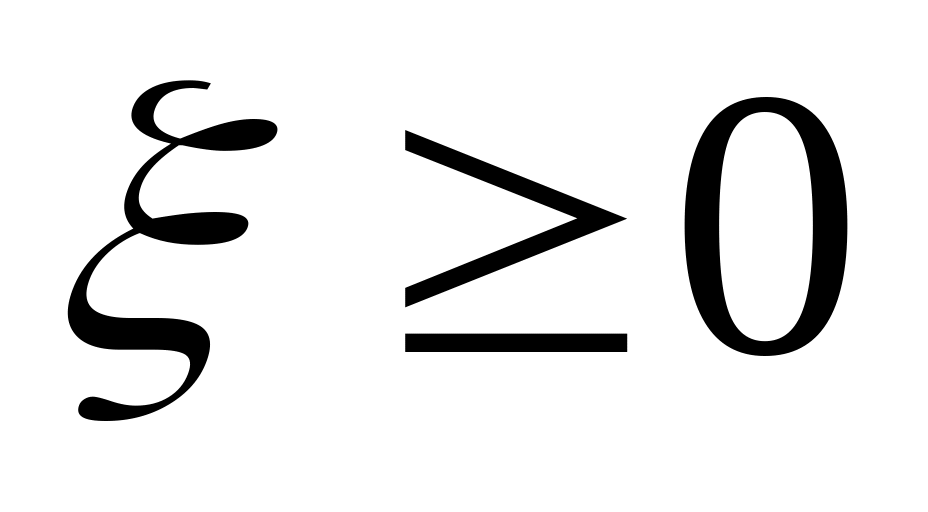 ,
then
,
then
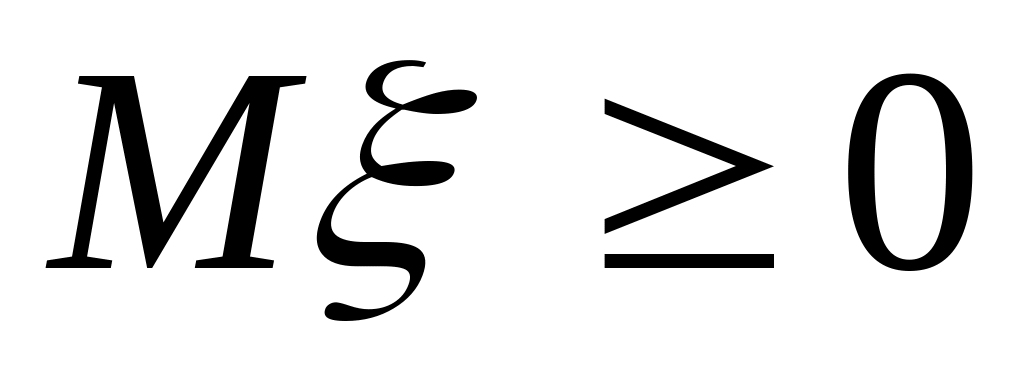 .
.If
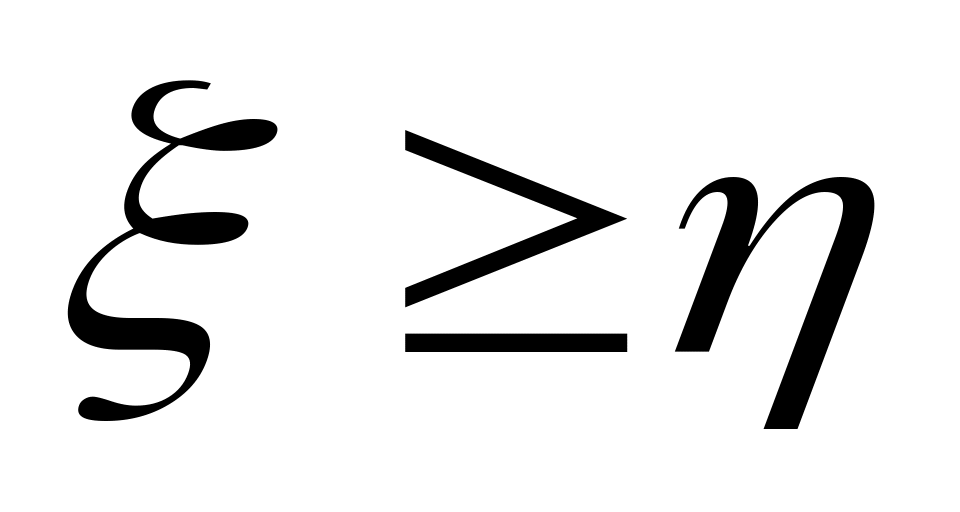 ,
then
,
then
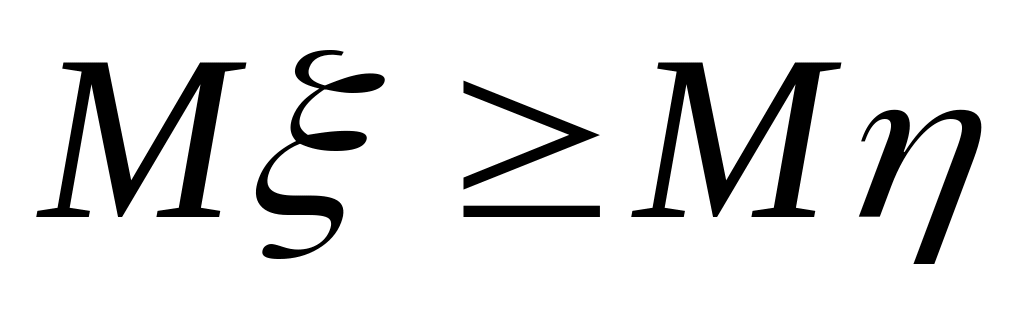 .
.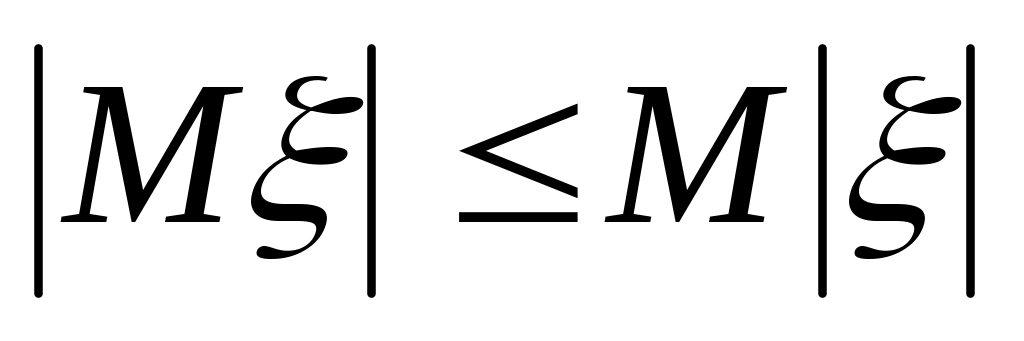 .
.
Mathematical expectation and average of a random variable
Let
be a finite random variable with values
![]() and values occur with the following frequencies:
occurs
and values occur with the following frequencies:
occurs
![]() times,
occurs
times,
occurs
![]() times,…,
times,…,
![]() occurs
occurs
![]() times. Then
times. Then
![]()
is the
average of values
![]() .
.
Definition
11.9 Numbers
![]() are relative frequencies of
.
are relative frequencies of
.
![]() .
.
So the interpretation of is the average.
Dispersion of a random variable
Definition 11.10 A dispersion of a random variable is the number
![]() .
.
Remark 11.4
![]() .
.
Properties of dispersion
1.
![]() .
.
2. If c
is
a constant, then
![]() .
.
3. If c
is
a constant, then
![]() ..
..
4. If c
is
a constant, then
![]() .
.
5. If
and
are
independent random variables![]()
Definition
11.11 The
number
![]() is called the standard deviation of
.
is called the standard deviation of
.
