Тақырып №1. Эконометрика негіздері

Эконометрика – бұл мақсаты экономикалық қатынастарға сандық шамалар беру болып табылатын ғылымның тез дамып келе жатқан саласы болып табылады.

Эконометрика – бұл экономикалық құбылыстар мен процестердің өзара қарым-қатынастарына сандық көрініс беретін ғылым.

Эконометрикалық зерттеулерге статистикалық көрініс беру басымдылыққа ие болды.

Эконометрикалық әдістің пайда болуы мен дамуы жоғары деп аталатын статистиканың негізінде – жұп және көптік регрессия, жұп, көптік және жеке корреляция, трендті және уақыт қатарының басқа да компоненттерін ажырату, статистикалық бағалау әдістерінің негізінде жүріп келді.

Эконометрикалық әдіс классикалық статистикалық әдістерді пайдалану нәтижелерін бұрмалайтын келеңсіздіктерден өтуде қалыптасады (мультиколлинеарлылық, автокорреляция, гомоскедастиктілік, ассимметриялылық, жалған корреляция, лагтардың болуы).

Эконометрика- эконмикалық өлшемдер туралы ғылым. Эконометрика 1) экономикалық теория, 2) математикалық және экономикалық статистика, 3) математика үш ғылымның өзара үйлесуінен тұрады.

Эконометрикада экономикалық процесстер мен құбылыстарды талдау эмпирикалық мәліметтер арқылы құрылған математикалық модельдер көмегімен жүзеге асырылады.

Эконометрика көмегімен есептің бір топ мәселелерін шығарады. Оларды үш белгілері бойынша классификациялауға болады:

1. түпкі қолданбалы мақсаты бойынша:

а) зерттелетін жүйенің дамуын және жағдайын анықтайтын әлеуметтік-экономикалық көрсеткіштерді болжау;

б) тұтас алғанда жүйенің жағдайына ең қуатты әсер ететін параметрлерді анықтау үшін жүйенің әлеуметтік-экономикалық дамуының мүмкін болатын түрлерін модельдеу;

2) иерархия деңгейі бойынша:

а) макродеңгейде шешілетін есептер (тұтас мемлекет);

б) мезодеңгейде шешілетін есептер (аудан, аймақ деңгейлері);

в) микродеңгейде шешілетін есептер (фирма, отбасы, кәсіпорын деңгейлері);

3) экономикалық жүйенің зерттелетін мәселелерін шешу салалары бойынша:

а) нарық;

б) инвестициялық, әлеуметтік, қаржылық саясат;

в) бағақалыптастыру;

г) бөліп тұратын қатынас;

д) сұраныс және тұтыну;

е) жеке шығарылған мәселелер кешені.

Кезкелген экономикалық модельдерде соңғы қолданбалы мақсаттарға тәуелді ондағы барлық қатысатын өзгермелілер келесідей бөлінеді:

• экзогенді, яғни нақты дәрежеде басқарылатын (жоспарланатын), автономды, «сырттан» беріледі;

• эндогенді, яғни, бір-бірімен өзара әрекеттес, экзогенді өзгермелілердің әсерінен, маңызды шамада талданатын әлеуметтік – экономикалық жүйенің функционалдануы ішінде және процесте атқарылатын ролі қалыптасатын өзгермелілер, ол эконометрикалық модельде түсіндіруші пән болып табылады;

• алдын – ала анықталған яғни факторлар – аргументтер ролінде немесе түсіндіруші өзгермелі ролінде жүйеде қатысушы.

Эконометрикалық модель экзогенді және лагтік эндогенді өзгермелілер мәнінен тәуелді эндогенді өзгермелілердің сипатын түсіндіру үшін қызмет көрсетеді деп айтуға болады.

Негізгі әдебиеттер: 1-3

Қосымша әдебиеттер: 1

Тақырып № 2. Регрессия-корреляциялық талдаудың математикалық негіздері

Жұптық сызытық регрессия (алдындағы тренд) - түріндегі теңдеу болып табылады, мұндағы а және в – регрессия параметрлері, ал - теңдеудің түпкі мәні (кездейсоқ шама). Модельде - нің пайда болуы: модельдің ерекшелігімен; мәліметтердің іріктелу сипатымен; өзгермелілердің ерекшеліктерімен тығыз байланысты.

Сызықтық тренд параметрлерін есептеу үшін теңдеудің келесідей жүйесі қолданылады:

.

Екі теңдеудің n – бөлеміз:

.

Алынған жүйедегі бірінші теңдеуден табамыз. Параметр мәнін екіші алынған жүйеге қоя отырып, аламыз. Аяғында трендтің екінші параметрін аламыз:

.

, ал мұндағы - трендтің белгілерінің ковориациясы, ал - Х белгісінің дисперсиясы.

В параметрін табу формуласын келесідей көрсетуге болады:

.

Трендтің іріктеу сапасы үшін кореляцияның сызықтық коэффициентінің квадраты есептеледі (детерменация коэффициенті [К^Д]). Бұл коэффициент нәтижелі белгінің дисперсиясында регрессиямен түсіндірілетін нәтижелі белгі дисперсиясының үлесін сипаттайды. Бұл коэффициент келесі формула бойынша есептеледі:

.

Осыдан және, егер , онда Ү өзгерісі Х өзгерісіне негізделген. Егер де , онда Ү өзгерісі немен болса да негізделеді, бірақ Х өзгерісімен емес.

формуласы бойынша алынған шама белгісіздіктің коэффициенті деп аталады. Бұл коэффициент (процентпен) Х – тан Ү тәуелділігін түсіндіруге болмайтын нәтижелі белгінің жалпы дисперсиясының үлесін көрсетеді.

Экономикада байланыс тығыздығын бағалау үшін корреляция (r) коэффициенті қолданылады. Бұл коэффициентті есептеу үшін әр түрлі формулалар балады. Олардың екеуін көрсетейік:

1.

2.

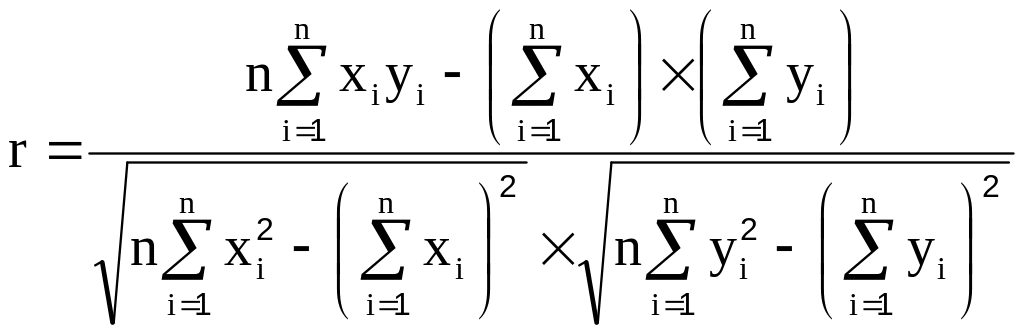
Әдетте, жақындық критерийі ретінде тәуелді айнымалының нақты мәндері -мен регрессия теңдеуі бойынша есептелген теоретикалық мәндердің айырмасының қосындыларының квадраттарының минимумы алынады:

,

мұндағы регрессия теңдеуі бойынша есептелген мәндер; - бақылау деректері; - белгісіз параметрлер.

функциясы үздіксіз, дөңес және төменгі жағынан нөлмен шектелген, яғни минимумы бар функция. Бұл әдісті ең кіші квадраттар әдісі (ЕКӘ) деп атайды.

Регрессия теңдеуінің маңыздылығын бағалау фишердің F – критер иі көмегімен беріледі. Осыдан нөлдік гипотеза (Н₀) жоғарылатылады, b=0 және сәйкесінше, Х факторы Ү факторына әсер етпейді. Бірақ одан бұрын дисперсиялық талдау жүргізген жөн. Ол үшін орта шамадан квадраттық ауытқудың жалпы сомасын екі бөлікке бөледі: (ауытқу квадратының жалпы соммасы = регрессиямен түсіндірілген ауытқу квадратының соммасы [факторлық сомма] + ауытқу квадратының қалған соммасы). Факторлық соммалар үшін еркін дәрежелер саны регрессиялар түрімен анықталады (сызықтық үшін 1-ге тең); сызықтық регрессия кезіндегі квадраттардың қалдық сомаларының еркін дәрежелер маны n-2-ге тең, ал еркін дәреженің жалпы саны n-1-ге тең.

Квадраттардың әрбір соммаларын еркін дәрежелер санына сәйкес бөле отырып, еркін дәрежесінің біреуін есептеу дәрежесін (D) аламыз:

1. ;

2. ;

3. .

Дисперсияның осындай түрін анықтау оның салыстырмалы түріне әкеледі.

Факторлық және қалдық дисперсияны салыстыра отырып F – критериді аламыз (F – қатынасы мөлшерін): . Егер Н₀ гипотезасы дұрыс болса, онда факторлы және қалдық дисперсиялар бір – бірімен ерекшеленбейді. Н₀ гипотизасын теріске шығару үшін алынған F – қатынасын Фишер – Снедекор кестесінен алынатын кестешелермен салыстыру қажет (маңыздылықтың түрлі деңгейлерінде) [k₁ - факторлық сомманың еркін дәрежесінің саны, k₂ – қалдық соммалардың еркін дәрежелерінің саны]. Егер нақты нәтижелер кестелерден көп болса, онда Н₀ гипотезасы ауытқиды, ал регрессия теңдеуі мәнділігін мойындайды.

Сенімді ықтималдылыққа жауап беретін шекаралар сенімді интервалдар деп аталады.

Үлестіру параметрлерін нүктелік бағалау белгісіз параметрдің мәніне жақын сан түрінде баға береді, мұндай бағалар өлшеулердің үлкен саны кезінде пайдаланылады. Практикада сенімді деп аталатын, нүктелік бағалау үшін интервалды анықтау қажет, оның шекараларының арасында бағаланатын параметрдің ақиқат мәні берілген сенімділікпен табылады.

P{x_н<x<x_в}=1-q,

мұнда q – маңыздылық деңгейі;

х_н және x_в – интервалдың төменгі және жоғарғы шекарасы.