28. Классификация жидкостей. Законы течения.

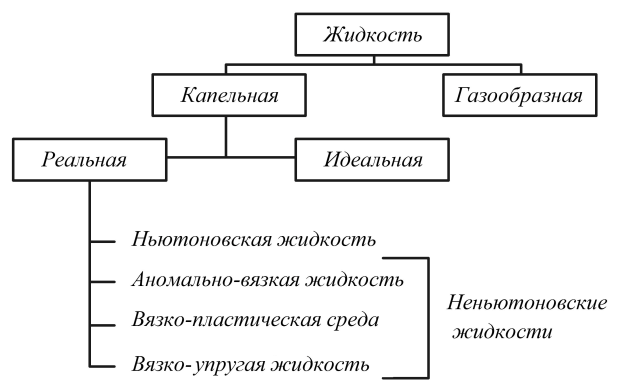
Газообразные жидкости под действием силы тяжести занимают весь объем сосуда, не имея поверхности раздела; сжимаемы, при этом сильно нагреваются, маловязкие.

Капельные жидкости, почти несжимаемые, под действием силы тяжести занимают объем сосуда, имея поверхность раздела

Идеальные жидкости абсолютно несжимаемы, молекулы этой жидкости обладают неограниченной свободой движения, следовательно – отсутствуют силы внутреннего трения, т.е. вязкость равна нулю.

Ньютоновская жидкость. Для случая одномерного течения молекулярный перенос импульса может быть представлен в виде: где  – напряжение сдвига,  – коэффициент динамический вязкости жидкости, – градиент скорости (скорость сдвига). Закону Ньютона подчиняются, в основном, низкомолекулярные жидкости.

Аномально-вязкие жидкости. Жидкости, вязкость которых зависит от гидродинамической ситуации, называются аномально-вязкими.

Аномально-вязкие жидкости, реологические характеристики которых зависят от времени.

Имеются материалы, для которых связь зависит от времени. Для этих материалов эффективная вязкость зависит не только от градиента скорости, но и от продолжительности сдвига.

Вязко-пластическая среда. Вязко-пластическая среда до напряжений ведет себя как твердое тело. С дальнейшим ростом  начинается вязкое (ньютоновское) течение. где  – коэффициент пластической вязкости.

Вязко-упругая жидкость. Вязко-упругая жидкость проявляет как упругое восстановление формы, так и вязкое течение. Вязко-упругие от вязких жидкостей отличаются также наличием обратимой деформации, они обладают памятью.

29. Особенности турбулентного движения жидкости. Касательные напряжения в турбулентном движении.

Хаотичное, неупорядоченное движение жидких частиц существенным образом влияет на характеристики турбулентных течений. Эти течения жидкости – неустановившиеся. Благодаря этому в каждой точке пространства скорости изменяются с течением времени. Мгновенное значение скорости можно выразить:

где – осредненная по времени скорость по направлению x, – пульсационная скорость по этому же направлению.

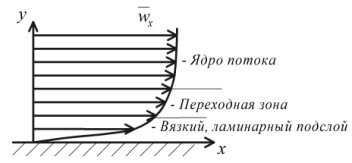
В ядре потока за счет пульсационных скоростей происходит непрерывное перемешивание жидкости. У твердых стенок поперечные движения частиц жидкости невозможны.

Около твердой стенки жидкость течет в ламинарном режиме.

Движение жидкости при турбулентном режиме всегда сопровождается значительно большей затратой энергии, чем при ламинарном.

Для определения контактного напряжения сил трения в турбулентном потоке используется формула: где – напряжение вязкого течения, – турбулентное напряжение, вызванное перемешиванием.

Как известно, определяется законом вязкого трения Ньютона:

Для горизонтальной прямой трубы в случае напорного течения вязкой жидкости критериальное уравнение имеет вид: где – геометрические комплексы, – критерий Рейнольдса, – критерий Эйлера. Они определяются как: где ∆ – абсолютная шероховатость трубы, l – длина трубопровода, d – внутренний диаметр трубы. Из опыта известно, что потери давления прямо пропорциональны . Поэтому можно записать:

Далее обозначим неизвестную функцию , распишем критерий Эйлера . Тогда из уравнения для потери давления получим: где  – коэффициент гидравлического трения, w – средняя скорость потока.

Полученное уравнение носит название уравнение Дарси – Вейсбаха. Уравнение (2.53) может быть представлено в виде потери напора: Таким образом, расчет потери давления или напора сводится к определению коэффициента гидравлического трения .

30. Давление, сжимаемость и поверхностное натяжение.

Предел отношения приращения силы к площади, при стремлении последней к нулю, называется гидростатическим давлением.

P=lim(<S->0)<F/<S.

1.Гидростатическое давление направлено всегда по внутренней нормали к площадке, на которую это давление действует.

2.Гидростатическое давление действует одинаково по всем направлениям, т.е. не зависит от угла наклона площадки, на которую оно действует

3. Гидростатическое давление в точке зависит от ее координат в пространстве, т.е. . Очевидно, что с увеличением глубины погружения точки давление в ней возрастает.

Сжимаемость - свойство жидкостей изменять свой объем при изменении давления - характеризуется коэффициентом объемного сжатия (сжимаемости), представляющим относительное изменение объема жидкости, при изменении давления на единицу: _{, [ Па}^-1 Знак (-) указывает на то, что положительному приращению давления (увеличению) соответствует отрицательное приращение (уменьшение) объема . Величина, обратная объемному коэффициенту сжатия, называется объемным модулем упругости жидкости. Закон Гука для идеальной жидкости:

Поверхностное натяжение-это свойство обуславливающееся силами взаимного притяжения, возникающими между частицами поверхностного слоя жидкости и вызывающими напряженное его состояние. Система, находящаяся в равновесии, занимает то из возможных для нее положений, которое соответствует минимуму энергии. Эти силы направлены по касательной и называются силами поверхностного натяжения. Коэффициент поверхностного натяжения можно выразить: , где - сила поверхностного натяжения, -длина линии, ограничивающая поверхность раздела. Сила поверхностного натяжение оказывает на жидкость дополнительное давление, нормальное к её поверхности, и может быть определена по формуле: , где - коэффициент поверхностного натяжения, - радиус трубки, в которой находится жидкость. Размерность - СИ [Н/м]. Благодаря действию поверхностного натяжения объем жидкости, на который не действуют никакие другие силы, принимают сферическую форму. С этим свойством связана способность жидкости образовывать капли.

31. Начальный участок. Распределение скорости по сечению круглой трубы.

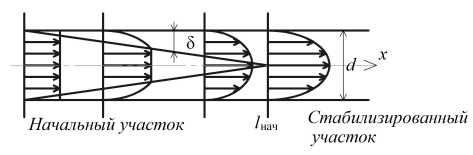
Участок трубы, на котором происходит стабилизация профиля скоростей, называется начальным участком или участком гидродинамической стабилизации, дальнейший участок – гидродинамически стабилизированным участком. На стабилизированном участке параметры потока не меняются.

33. Понятие о технико-экономическом расчете труб.

Оптимальный (наиболее экономически выгодный) диаметр определяется на основе технико-экономических расчетов.

Уменьшение диаметра трубопровода приводит к увеличению мощности насоса N_н; увеличение d – наоборот к уменьшению N_н. Но увеличение диаметра приведет к увеличению стоимости трубопровода и строительства трубопроводной сети. Итак, необходимо учитывать как затраты эксплуатационные, так и капитальные. Эксплуатационные затраты : расход электроэнергии на работу насоса, обслуживание трубопроводной сети, ремонт сети и управленческие расходы. Капитальные затраты : стоимость насоса и трубопроводов, стоимость сооружений и амортизационные расходы. Полная стоимость варианта трубопроводной сети: , где t – срок окупаемости сооружения. Обычно лет.

Таким образом, задача определения оптимального диаметра трубопровода сводится к определению минимума полной стоимости трубопроводной сети С. Задача может быть решена разными методами:

– математический (определение минимума функции С);

– графический;

– подбор вариантов.