
- •Корреляционный и регрессионный анализ трехмерной генеральной совокупности Исходные данные
- •I. Корреляционный анализ Постановка задачи
- •Нахождение границ доверительных интервалов для математических ожиданий arcth(rxy/z), arcth(rxz/y), arcth(ryz/X)
- •Сопоставление частных и парных коэффициентов корреляции
- •4. Исследование множественных коэффициентов корреляции
- •Анализ качества модели регрессии
- •Проверка значимости уравнения множественной линейной регрессии
- •Несмещенная оценка остаточной дисперсии
Анализ качества модели регрессии
Необходимо, установить, соответствует ли эмпирическим данным построенная математическая модель:
![]() ,
,
а также определить, достаточно ли включенных в уравнение объясняющих переменных (предикторов) для описания зависимой (критериальной) переменной.
Проверка значимости уравнения множественной линейной регрессии
(при уровне значимости применяемого статистического критерия α=0,05)
Основная гипотеза: «Уравнение регрессии не значимое»:
![]() .
.
Для определения значения статистики критерия Фишера:

вычисляется вектор
 ,
,
находится сумма квадратов расчетных средних значений признака Z:
![]() .
.
вычисляется вектор ошибок наблюдений (остатков):
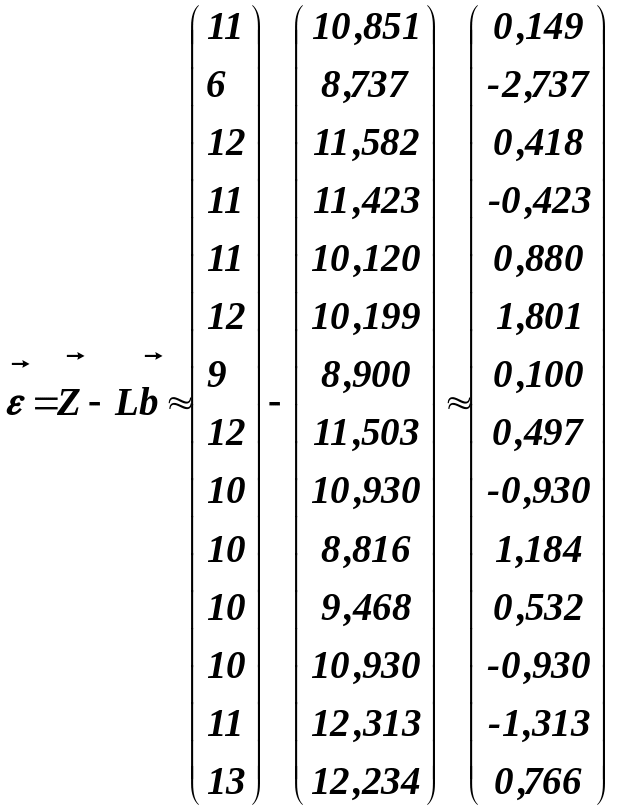 .
.
определяется остаточная сумма квадратов отклонений фактических значений признака Z от соответствующих расчетных средних значений, найденных на основе уравнения регрессии Z на (X, Y) - квадрат длины вектора ошибок наблюдений, обусловленных воздействием случайных факторов:
![]() .
.
Получаем
![]()
![]() .
.
Граничное
(критическое) значение
![]() определяется согласно уравнению:
определяется согласно уравнению:
![]() ,
,
принимающему в данном случае следующий вид:
![]() .
.
Используя статистическую таблицу 4 (Распределение Фишера – Снедекора) находим
![]() .
.
Условие отвержения
основной гипотезы:
![]() выполняется,
следовательно, при уровне
выполняется,
следовательно, при уровне
![]() уравнение регрессии значимое, т.е.
можно
заключить, что с вероятностью, равной
0,95,
хотя бы один из коэффициентов β1,
β2
существенно отличается от нуля.
уравнение регрессии значимое, т.е.
можно
заключить, что с вероятностью, равной
0,95,
хотя бы один из коэффициентов β1,
β2
существенно отличается от нуля.
Несмещенная оценка остаточной дисперсии
![]() .
.
