Плоское живое сечение
мал
Рассмотрим закон изменения давления по живому сечению при плавноизменяющемся движении.
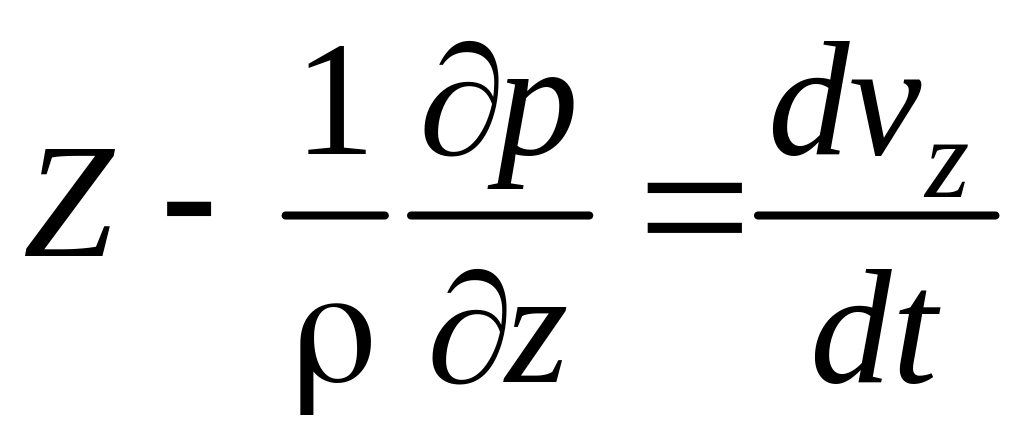
Выберем систему координат таким образом, чтобы ось x совпадала со скоростью v, а живое сечение было бы расположено в плоскости ZOY.
Тогда
,
,
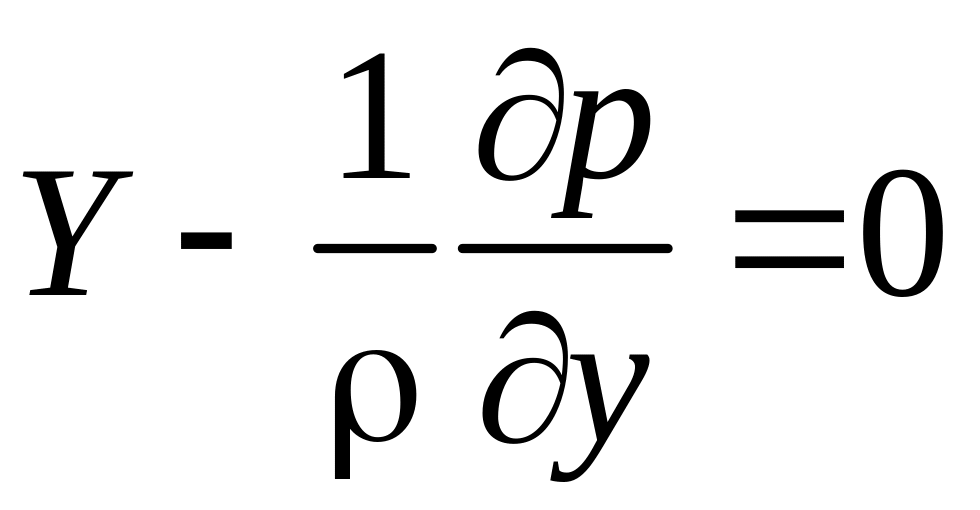
Рассмотрим движение жидкости в поле сил тяжести при постоянном давлении в направлении y.
Давление в живом
сечении при плавноизменяющемся движении
изменяется в направлении z
по основному закону гидростатики.
Уравнение Бернулли для реального потока.
Рассмотрим установившееся и плавноизменяющееся движение потока жидкости.
При рассмотрении движения потока реальной жидкости необходимо учитывать:
1. Вязкость жидкости, которая приводит к возникновению касательных напряжений, на преодоление которых затрачивается энергия.
2. Неравномерность распределения скорости по сечению.
- полная энергия
жидкости в элементарной струйке
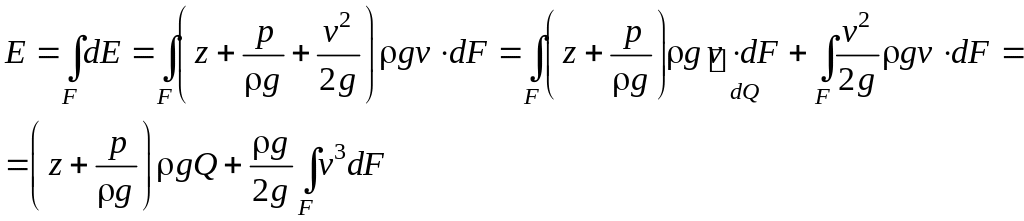
Найдем значение удельной энергии потока в рассматриваемом живом сечении:
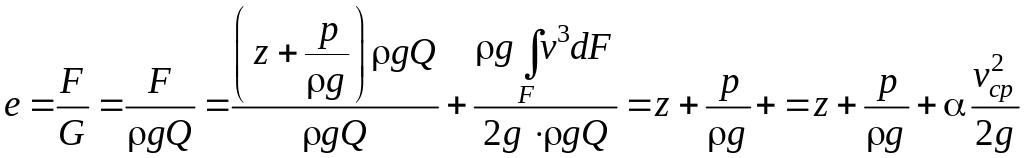
при обычном
распределении скоростей
при равномерном
распределении скоростей
при ламинарном
режиме
при турбулентном
режиме
Отношение
кинетической энергии при действительном
распределении скоростей по живому
сечению к кинетической энергии, взятой
по средней скорости
- потери удельной
энергии жидкости на участке 1 – 2.
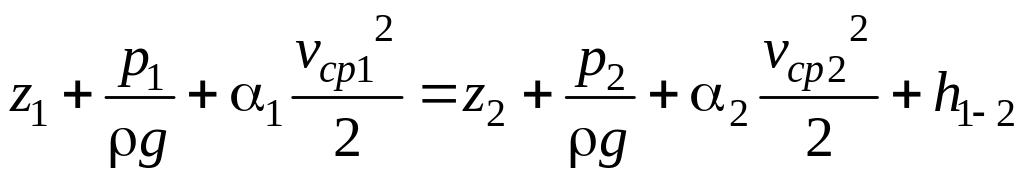– уравнение
Бернулли для реального потока жидкости.
складывается из
1. потерь, вызванных деформацией потока и вихреобразованием
2. потерь на трение.
,
где
- коэффициент местного сопротивления.
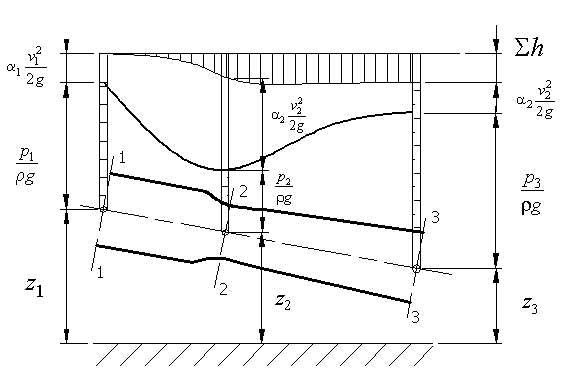
Уравнение Бернулли для реального потока представляет собой уравнение баланса энергии с учетом потерь.
Уменьшение среднего значения полной удельной энергии жидкости вдоль потока, отнесенное к единице его длины, называется его гидравлическим уклоном.
Практическое применение уравнения Бернулли.
Трубка полного напора.
Трубка Пито-Прандтля.
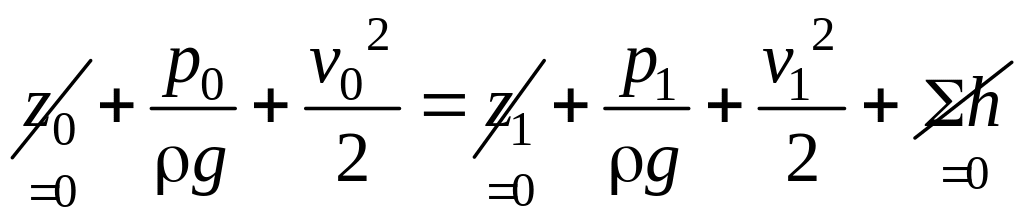
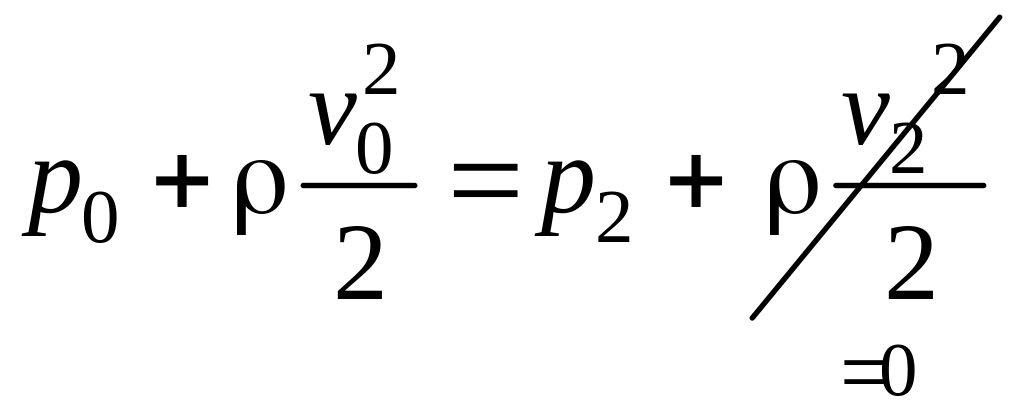
Так как отверстия
трубки воспринимают давление
невозмущенного потока,
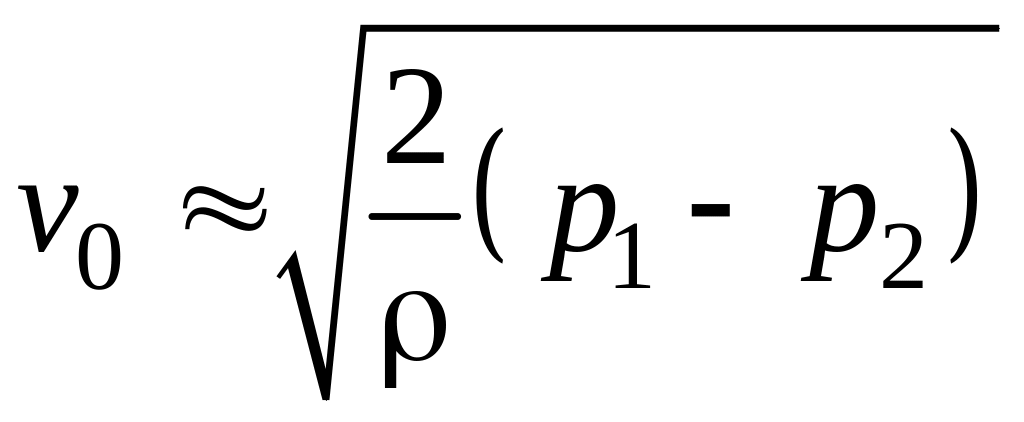
Дроссельные расходомеры.
труба Вентури
сопло
диафрагма
Рассмотрим работу дроссельного расходомера на примере диафрагмы.
Для определения
зависимости
от
запишем уравнение Бернулли для сечений
11 – 22.
,
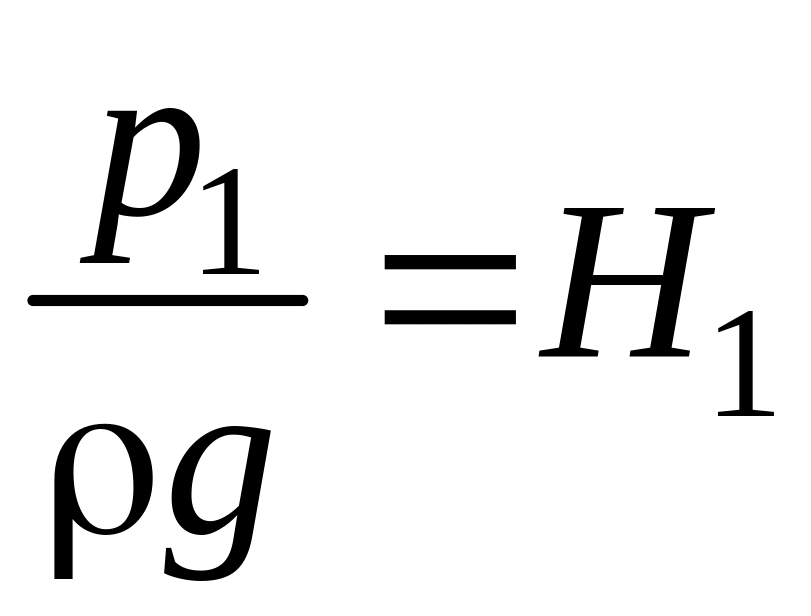- коэффициент
сжатия трубы
– коэффициент
скорости
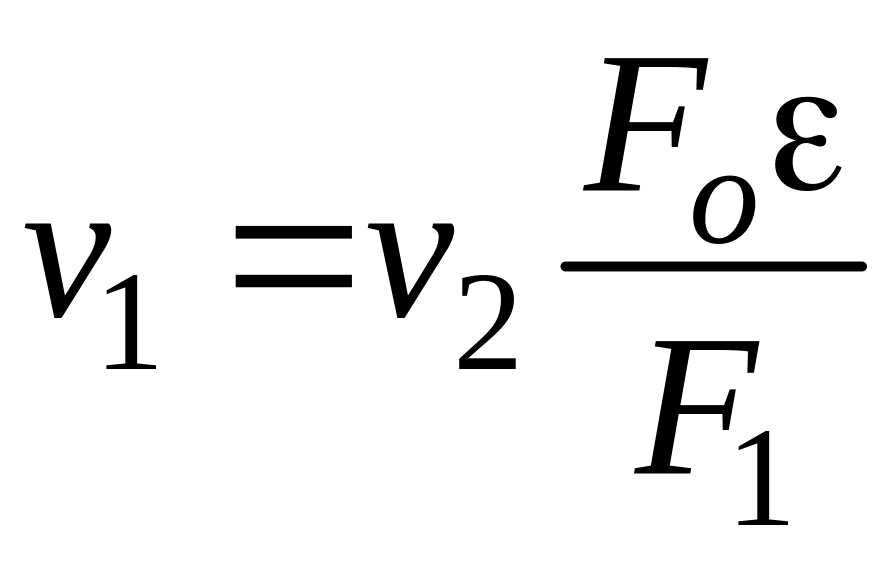
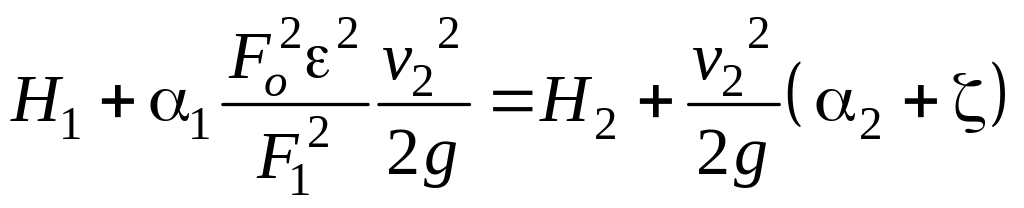
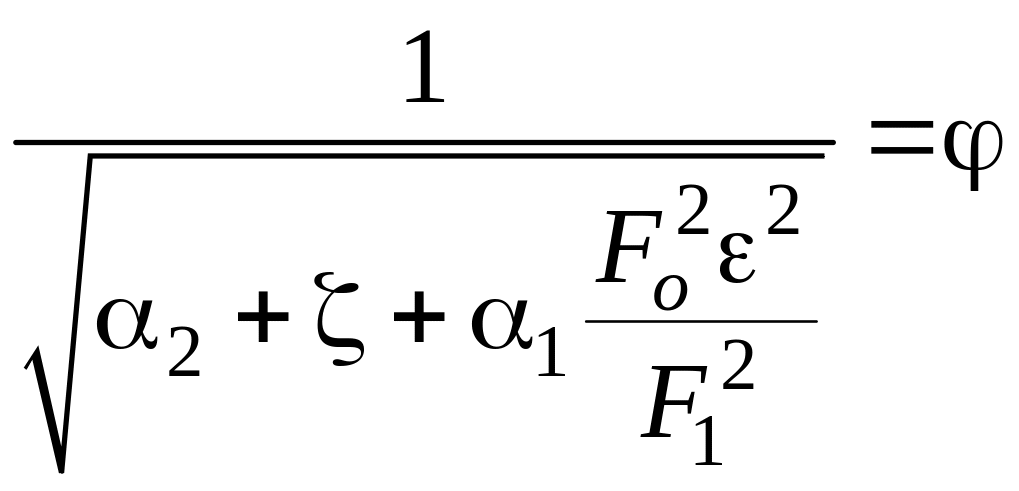- коэффициент
расхода
Так как коэффициенты
и
определить теоретически с достаточной
степенью точности нет возможности, то
необходимо проводить тарировку
дроссельного расходомера.
Тарировкой называет
эксперимент, определяющий зависимость
,
а также зависимость
.
Re – число Рейнольдса.
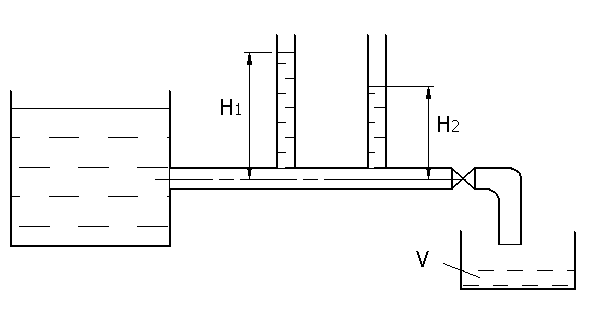
Методика тарировки дроссельных расходомеров.
где Q – расход
–
время наполнения
где
– вязкость – является функцией
температуры, которую нужно измерять в
течение эксперимента
d – диаметр
– турбулентный
режим (вода, керосин)
– ламинарный
режим (масла)
Ламинарное – такое течение , при котором не происходит перемешивания слоев жидкости и нет пульсаций скорости.
Турбулентное – течение, сопровождающееся интенсивным перемешивание слоев жидкости, наличием пульсаций скорости и давления.