4. Оценка тесноты связи признаков в модели парной линейной регрессии. Коэффициент корреляции.

Парная линейная регрессия – линейная связь между двумя переменными x и y (описывается в виде прямой), уровнение y = a + bx, где b – коэффициент регрессии, a – свободный член уравнения регрессии.

Оценка тесноты связи признаков в модели парной линейной регрессии происходит с использованием коэффициента корреляции.

Корреляция — взаимосвязь двух или нескольких случайных величин. При этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции. Коэффициент корреляции – это показатель характера взаимного влияния изменения двух случайных величин. Обозначается буквой R и принимает значение от -1 до +1. Если значение по модулю находится ближе к 1 – это означает наличие сильной связи, а если ближе к 0 – связь слабая или вообще отсутствует. Коэффициент корреляция может быть положительным и отрицательным. Отрицательная корреляция – увеличение одной переменной связано с уменьшением другой переменной. Положительная корреляция – увеличение одной переменной связано с увеличением другой переменной.

Корреляции м.б. найден как индекс множ. корреляции:

,

где -общая дисперсия результатного признака;

-остаточная дисперсия для уравнения y=f(Х₁,Х₂,…,Х_Р).

Дисперсия – это отклонение значений случайной величины относительно среднего значения.

5. Проверка качества уравнения регрессии с помощью f-теста (f-критерия) Фишера.

Оценка значимости уравнения в целом проверяется с помощью критерия Фишера.

Выдвегается нулевая гипотеза о том, что коэффициент регрессии b=0.

Если найденное значение Фишера > табличного, то нулевая гипотеза (об отсутствии связи признака) отклоняется и делается вывод о сущности этой связи (т.е. это уравнение можно учитывать в дальнейших исследованиях).

Если найденное значение Фишера < табличного, то нулевая гипотеза (об отсутствии связи признака) не отклоняется и делается вывод о незначимости уравнения (т.е. это уравнение можно не учитывать в дальнейших исследованиях).

,

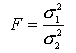где - большая дисперсия, - меньшая дисперсия.

Дисперсия – это отклонение значений случайной величины относительно среднего значения.

6.Применение t-теста для оценки значимости параметров уравнения регрессии.

Для оценки сущности параметров рассчитывается коэффициент Стьюдента.

С этой целью по каждому из параметров определяется его стандартная ошибка: M_b и M_a.

Стандартная ошибка коэффициента регрессии определяется по формуле:

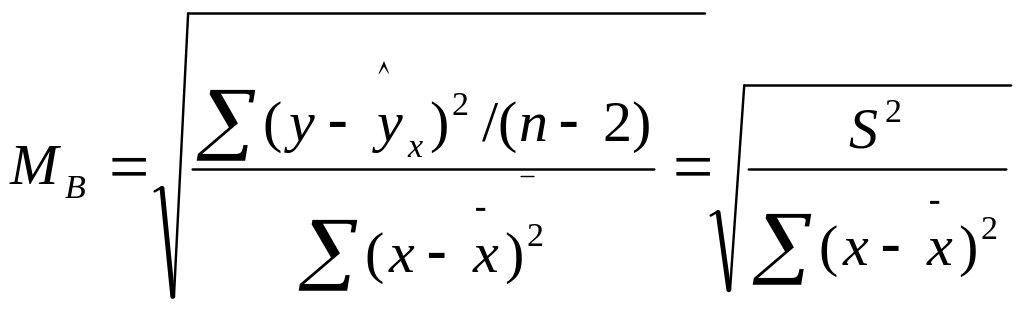
Где S² –остаточная дисперсия на одну степень свободы,

_{-сумма квадратов.}

Для оценки существенности коэф-та регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t- критерия Стьюдента:

, которое затем сравнивается с табличным(если критерий Стьюдента фактический > критерия Стьюдента табличного, то коэффициент значимый).