4.Оценка тесноты связи признаков в модели регрессии. Коэффициент корреляции.

Коэф-нт корреляции бывает множественный и частный. Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата-коэффициента детерминации. Показатель множ. корреляции характеризует теснту связи рассматриваемого набора факторов с исследуемым признаком. Независимо от формы связи показатель множ. Корреляции м.б. найден как индекс множ. корреляции: , где -общая дисперсия результатного признака; -остаточная дисперсия для уравнения y=f(Х₁,Х₂,…,Х_Р). Расчет индекса множ. корреляции предполагает определение уравнения множ. регрессии и на его основе остаточной дисперсии: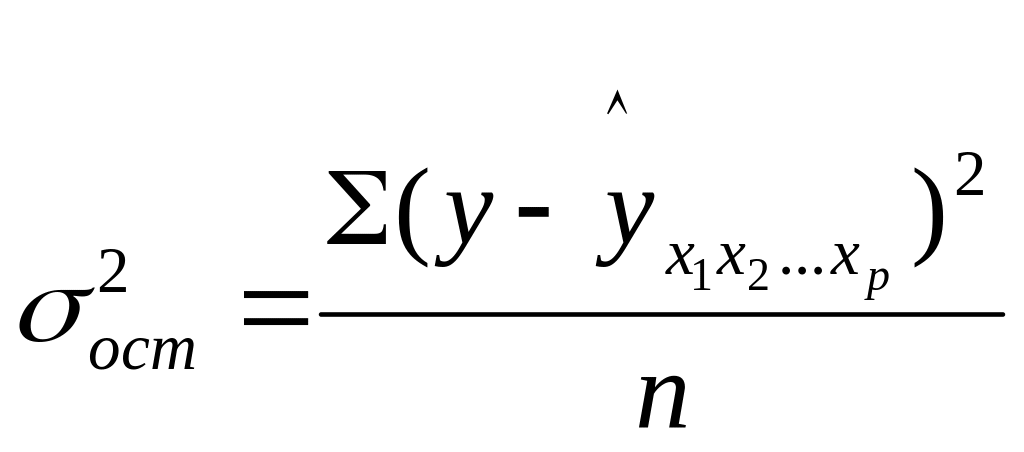 , -расчетное.

5. F-тест или F-критерий Фишера на качество уравнения регрессии.

После того, как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэф-нт регрессии=0, и фактор Х не оказывает влияния на результат У. Непосредственно расчету F-критерия предшествует анализ дисперсии:

При расчете суммы квадратов используются теоретические значения результативного признака , найденные по линии регрессии: . В линейной регрессии Сумма квадратов отклонений, обусловленных линейной регрессией, составит:

Существуют равенство между числом степеней свободы общей, факторной и остаточной суммы квадратов при лин. регрессии составляет n-2. Число степеней свободы для общей суммы квадратов определяется числом единиц, т.к. мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы.

6.Применение f- теста для оценки значимости параметров уравнения регрессии.

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: M_b и M_a.

Стандартная ошибка коэффициента регрессии определяется по формуле: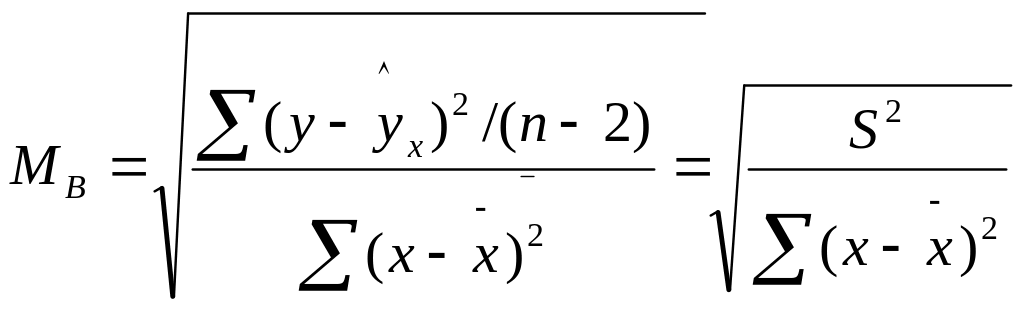

Где S² –остаточная дисперсия на одну степень свободы. Величина стандартной ошибки совместно с t-распределением Стьюдента при n-2 степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительных интервалов. Для оценки существенности коэф-та регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t- критерия Стьюдента: , которое затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n-2).

7.Доверительные интервалы для линейной функции регрессии и индивидуальных значений результативного признака. Аналитическая и геометрическая интерпретация.

8. Метод наименьших квадратов для оценки структурных параметров линейной регрессии.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

МНК позволяет получить такие оценки параметров а или b, при которых сумма квадратов отклонений фактических значений ре­зультативного признака (у) от расчетных (теоретических) ми­нимальна: (1)

Из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы min: следовательно,

Линия регрессии с минимальной дисперсией остатков.

Чтобы найти min функции (1), надо вычислить частные производные по каждому из параметров а и b и приравнять их к 0. Обозначим через S, тогда ;

(2)

Преобразуя формулу (2), получим след. систему нормальных уравнений для оценки параметров a и b:

(3)

Найдем оценки параметров а и b. Можно воспользоваться готовыми формулами: (4).

Формула (4) получена из первого уравнения системы (3), если все его члены разделить на n. где cov (x,y)-ковариация признаков, -дисперсия знака x. Ввиду того, что cov (x,y)= а , получим след. формулу расчета оценки параметра b:

Параметр b назыв. коэффициентом регрессии, его величина показывает среднее изменение результата с изменением фактора на одну единицу.