2. Функциональная и статистическая и корреляционная зависимости.

Некоторые методы математической статистики могут помочь любому специалисту выявить взаимосвязи, раскрыть их особенности. Одним из таких методов и является метод корреляционного анализа. Он направлен на то, чтобы на основе статистического материала выявить факт влияния одного признака на другой, установить полезность или вред этого влияния и оценить уверенность в полученных выводах. При этом различают два вида зависимости — функциональную и статистическую (корреляционную). Понятие функциональной зависимости

Будем говорить, что между двумя признаками X и Y существует функциональная зависимость (взаимосвязь), при которой каждому значению одного из них соответствует одно или несколько строго определенных значений другого.

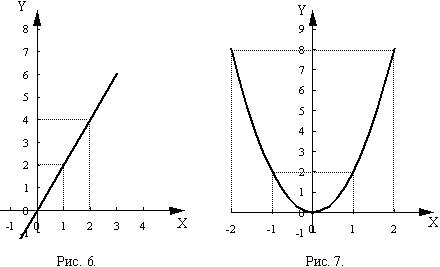
Например, в функции у = 2Х каждому значению Х соответствует в два раза большее значение у. В функции Y=2*X² каждому значению у соответствует 2 определенных значения х. Графически это выглядит так (рис. 6, 7 соответственно): Статистическая зависимость – это связь переменных, на которую накладывается воздействие случайных факторов, при этом изменение одной переменной приводит к изменению математического ожидания (т.е. наиболее вероятного ожидаемого значения) другой переменной.

Понятие корреляционной зависимости и ее направленности

Будем говорить, что между двумя признаками Х и У существует корреляционная зависимость (взаимосвязь), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака У, и наоборот.

Для различия направленности влияния одного признака на другой введены понятия положительной и отрицательной связи.

Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной.

Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной.

3. Виды регрессий. Общая характеристика парной линейной регрессии.

Парная регрессия делится на линейную и нелинейную. Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида: или Уравнение вида позволяет по заданным значениям фактора х иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х. На графике теоретические значения представляют линию регрессии (рис. 1).

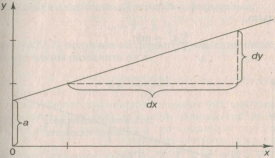Рис. 1. Графическая оценка параметров линейной регрессии

Построение линейной регрессии сводится к оценке ее параметров — а и b. Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию (см. рис. 1). Далее по графику можно определить значения параметров. Параметр а определим как точку пересечения линии регрессии с осью оу, а параметр b оценим, исходя из угла наклона линии регрессии, как dy/dx где dу — приращение результата у, а dx— приращение фактора х, т. е. .

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций

Различают два класса нелинейных регрессий: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции: 1)полиномы разных степеней- y=a + b * x + c-x² + e, y=a + b * x + c + c * x² + d * x³ + e

2) равносторонняя гиперболa – y=a+b/x+e.

К нелинейным регрессиям по оцениваемым параметрам относятся функции:1)степенная – y=a*x^b*e;

2)показательная – y=a*b^x*e;

3)экспоненциальная – y=e^a+b*x+e.

Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам.