Инкубатор Бабы Яги Условие
У Бабы Яги в избушке на курьих ножках есть инкубатор, в котором появляются куры с различным количеством ног. Ног может быть от одной до шести. Каждый день в инкубаторе появляется ровно одна курица.
В Научно-исследовательском институте сельскохозяйственных исследований, в котором Баба Яга по совместительству работает уборщицей, заинтересовались данным феноменом. Учёные поставили задачу исследования периодичности количества ног у кур с целью дальнейшего прогнозирования этого количества.
Сотрудники института собрали статистические данные. В течение нескольких дней они записывали количество ног у появившейся курицы.
Требуется по данным записям для каждого возможного количества ног определить наиболее часто встречающееся количество дней между последовательными появлениями куриц с таким количеством ног.
Формат входного файла
Входной файл содержит целое число N, за которым следуют N целых чисел от 1 до 6 — результаты измерений количества ног у кур в течение N дней.
Формат выходного файла
Выходной файл должен содержать 6 целых чисел — наиболее часто встречающиеся количества дней между появлениям одноногих, двуногих, трёхногих, четырёхногих, пятиногих и шестиногих кур. Если с таким количеством ног появилось менее двух кур, то соответствующее число в выходном файле должно быть 0.
Если решений несколько, вывести любое из них.
Ограничения
1 ≤ N ≤ 1000
Примеры тестов
-
№
Входной файл
Выходной файл
1
12
3 1 1 1 2 1 3 2 2 5 6 2
1 3 6 0 0 0
2
10
3 6 3 6 2 3 2 6 3 2
0 2 3 0 0 4
Разбор
Будем решать задачу по очереди для одноногих, двуногих, трёхногих, четырёхногих, пятиногих и шестиногих кур. Будем просматривать исходный массив. Переменная x будет хранить индекс последнего встретившегося числа, равного текущему количеству ног l. Переменная px будет хранить индекс предпоследнего встретившегося числа, равного текущему количеству ног. Переменные x и px легко обновляются:
if (a[i] = l) then
begin
px := x;
x := i;
end;
Тогда количество дней между последовательными появлениями кур с определённым количеством ног равно x-px. Осталось подсчитать, сколько раз встречается каждое возможное количество дней между последовательными появлениями кур с таким количеством ног. Для этого заполним массив cnt.
А затем найдём максимум в этом массиве.
program incubator;
const
MAX_N = 1000;
var
a: array[1..MAX_N] of integer;
cnt: array[1..MAX_N-1] of integer;
n: integer;
x, px: integer;
max, max_i: integer;
i, l: integer;
begin
assign(input, 'input.txt');
reset(input);
assign(output, 'output.txt');
rewrite(output);
read(n);
for i := 1 to n do
read(a[i]);
for l := 1 to 6 do
begin
for i := 1 to n-1 do
cnt[i] := 0;
x := 0;
px := 0;
for i := 1 to n do
begin
if (a[i] = l) then
begin
px := x;
x := i;
if ((x <> 0) and (px <> 0)) then
inc(cnt[x-px]);
end;
end;
max := 0;
for i := 1 to n-1 do
begin
if (cnt[i] > max) then
begin
max := cnt[i];
max_i := i;
end;
end;
if (max = 0) then
write(0, ' ')
else
write(max_i, ' ');
end;
close(input);
close(output);
end.
Сумма 0, произведение N
Условие
Дано целое число N, кратное 4. Требуется найти N целых чисел, сумма которых равна 0, а произведение равно N.
Формат входного файла
Входной файл содержит единственное целое число N.
Формат выходного файла
Требуется вывести N чисел — ответ в задаче. Числа выводить в произвольном порядке.
Если искомых чисел не существует, то выходной файл должен содержать единственное число 0.
Если существует несколько решений, вывести любое из них.
Ограничения
4 ≤ N ≤ 1000
Примеры тестов
-
№
Входной файл
Выходной файл
1
4
2 1 -1 -2
Разбор
Рассмотрим случай, когда N делится на 8. Выберем следующие числа:
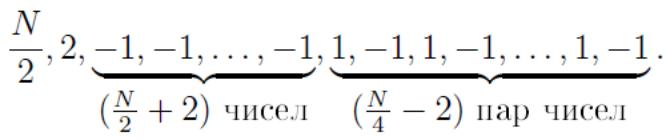
Нетрудно видеть, что всего здесь N чисел, причём их сумма равна 0, а произведение равно N.
Рассмотрим случай, когда N не делится на 8. Выберем следующие числа:
Всего здесь N чисел, причём их сумма равна 0, а произведение равно N.
program sum_product;
var
n: integer;
i: integer;
begin
assign(input, 'input.txt');
reset(input);
assign(output, 'output.txt');
rewrite(output);
read(n);
if (n mod 8 = 0) then
begin
write(n div 2, ' ', 2, ' ');
for i := 1 to n div 2 + 2 do
write(-1, ' ');
for i := 1 to n div 4 - 2 do
write(1, ' ', -1, ' ');
end
else
begin
write(n div 2, ' ', -2, ' ');
for i := 1 to n div 2 - 2 do
write(-1, ' ');
for i := 1 to n div 4 do
write(1, ' ', -1, ' ');
end;
close(input);
close(output);
end.
Отрезки с наложением
Условие
Дано N отрезков с длинами w1, …, wN. Требуется расположить их на интервале числовой оси [0, L] так, чтобы они покрыли этот интервал без пропусков и не выходили за его границы.
Необходимо использовать все отрезки. Отрезки можно накладывать друг на друга.
Формат входного файла
Первая строка входного файла содержит целые числа N и L.
Вторая строка содержит N целых чисел w1 w2… wN.
Формат выходного файла
Выходной файл должен содержать N целых чисел x1 x2 … xN — координаты левых концов отрезков.
Если решения не существует, то выходной файл должен содержать единственное число −1. Если существует несколько решений, вывести любое из них.
Ограничения
1 ≤ N ≤ 1000
1 ≤ L ≤ 10000
1 ≤ wi ≤ 10000
Примеры тестов
-
№
Входной файл
Выходной файл
1
2 3
2 2
0 1
Разбор
Если сумма всех wi меньше L или максимальное wi больше L, то покрыть отрезок длиной L невозможно.
Иначе расположим отрезки следующим образом. Пока сумма длин размещённых отрезков меньше L, координату левого конца следующего отрезка будем выбирать равной координате правого конца предыдущего отрезка. Если при добавлении очередного отрезка сумма длин отрезков становится больше L, то этот отрезок располагаем так, чтобы координата его правого конца равнялась L.
program intervals;
var
w, x: array[1..1000] of integer;
n, l: integer;
sum, max: integer;
i: integer;
begin
assign(input, 'input.txt');
reset(input);
assign(output, 'output.txt');
rewrite(output);
read(n, l);
sum := 0;
max := 0;
for i := 1 to n do
begin
read(w[i]);
sum := sum + w[i];
if (w[i] > max) then
max := w[i];
end;
if ((sum < l) or (max > L)) then
write(-1)
else
begin
x[1] := 0;
for i := 2 to n do
begin
if (x[i-1] + w[i-1] + w[i] <= l) then
x[i] := x[i-1] + w[i-1]
else
x[i] := l - w[i];
end;
for i := 1 to n do
write(x[i], ' ');
end;
close(input);
close(output);
end.