7.1 Физика процесса движения газожидкостной смеси в вертикальной трубе.

При скважинной добыче нефти практически всегда происходит выделение газа. Для понимания механизмов подъема жидкости из скважин, для проектирования установок подъема и выбора необходимого оборудования, надо знать законы движения газожидкостных смесей (ГЖС) в трубах.

Качественную характеристику процесса движения газожидкостной смеси в вертикальной трубе легче уяснить из следующего простого опыта (рис. 1).

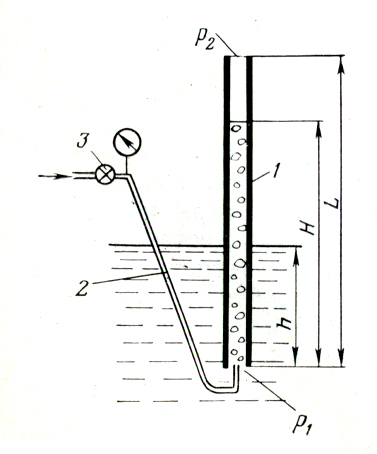
Рисунок 1. Схема газожидкостного подъемника

Здесь трубка 1 длиною L погружена под уровень жидкости неограниченного водоема на глубину h. К нижнему открытому концу трубки, который по аналогии с промысловой терминологией называется башмаком, подведена другая трубка 2 для подачи с поверхности сжатого газа. На трубке имеется регулятор расхода 3, с помощью которого можно установить желаемый расход газа.

Давление у башмака подъемной трубки 1 будет равно гидростатическому на глубине h, т.е. р₁=ρgh, и не будет изменяться от того, много или мало газа подается к башмаку. По трубке 2 подается газ, и в трубке 1 создается газожидкостная смесь средней плотности ρ_с , которая поднимается на некоторую высоту H. Поскольку внутренняя полость трубки 1 и наружная область являются сообщающимися сосудами, имеющими на уровне башмака одинаковые давления, то можно написать равенство

,

откуда

. (1)

Плотность смеси в трубке ρ_с зависит от расхода газа V. Чем больше V, тем меньше ρ_с . Следовательно, изменяя V, можно регулировать H. При некотором расходе V=V₁ величина H может достигнуть L. При V<V₁ H<L. При V>V₁ H>L и наступит перелив жидкости через верхний конец трубки 1. При дальнейшем увеличении V расход поступающей на поверхность жидкости q увеличится. Однако при непрерывном увеличении V расход жидкости не будет увеличиваться непрерывно, так как под воздействием неизменяющегося перепада давления ( , так как ), труба определенной длины L и диаметра d должна пропускать конечное количество жидкости, газа или газожидкостной смеси. Таким образом, при некотором расходе газа V=V₂ дебит достигает максимума .

Возможен другой крайний случай, когда к башмаку подъемной трубы подводится так много газа, что при постоянном перепаде давления будет идти только газ, и будет расходоваться на преодоление всех сопротивлений, вызванных движением по трубе чистого газа. Расход этого газа пусть будет V=V₃ . Если к башмаку подать еще больший расход (V>V₃), то излишек газа не сможет пройти через подъемную трубу, так как ее пропускная способность при данных условиях (L, d, Δp) равна только V₃, и устремится мимо трубы, оттесняя от башмака жидкость. При этом расход жидкости будет равен нулю (q=0). Таким образом, из этого опыта можно сделать следующий вывод.

1. При V<V₁ q=0 (H < L).

2. При V=V₁ q=0 (H=L) (начало подачи).

3. При V₁<V<V₂ 0<q<q_max (H>L).

4. При V=V₂ q=q_max (точка максимальной подачи).

5. При V₂<V<V₃ 0<q<q_max.

6. При V=V₃ q=0 (точка срыва подачи).

Обычно правая ветвь кривой q(V) (рис. 2) пологая, левая крутая. Для всех точек кривой постоянным является давление p₁, так как погружение h в процессе опыта не изменялось. Существует понятие – относительное погружение ε=h/L. Таким образом, для данной кривой ее параметром будет величина относительного погружения ε.

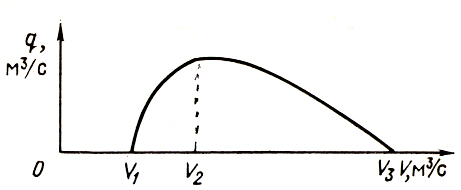
Рисунок 2. Зависимость подачи q газожидкостного подъемника от расхода газа V

Определим зависимость положения кривых q(V) от погружения. Поскольку на величину ε никаких ограничений не накладывалось, то при любых ε, лежащих в пределах 0<ε<1, вид соответствующих кривых q(V) будет одинаковый. При увеличении ε новые кривые q(V) обогнут предыдущие, так как с ростом h потребуется меньший расход газа для наступления перелива. По тем же причинам возрастет q_max , а точка срыва подачи на соответствующих кривых сместится вправо. При уменьшении ε все произойдет наоборот. Новые кривые q(V) расположатся внутри прежних и при ε=0 кривая q(V) выродится в точку. Другой предельный случай ε=1 (h=L; 100% погружения). В этом случае при бесконечно малом расходе газа произойдет перелив. Точка начала подачи сместится в начало координат. Кривая q(V) для ε=1 начнется в начале координат и обогнет все семейство кривых. Таким образом, каждый газожидкостный подъемник характеризуется семейством кривых q(V), каждый из которых будет иметь свой параметр ε (рис. 3).

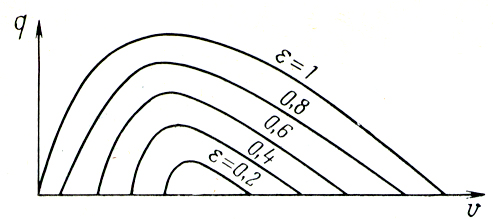
Рисунок 3. Семейство кривых q(V) для газожидкостного

подъемника данного диаметра

Определим зависимость кривых q(V) от диаметра трубы. Поскольку никаких ограничений на диаметр подъемной трубы и на ее длину не накладывалось, то аналогичное семейство кривых q(V) должно существовать для подъемников любого диаметра и любой длины. Каким образом расположится новое семейство кривых для трубы диаметром d₂>d₁ по отношению к прежним кривым. Увеличение диаметра потребует большого расхода газа, так как объем жидкости, который необходимо разгазировать для достижения данной величины ρ_с, при прочих равных условиях (h=const, L=const) возрастает пропорционально d². Пропускная способность трубы по жидкости, газу или газожидкостной смеси также возрастает. Поэтому для увеличенного диаметра будет существовать также семейство кривых q(V), все точки которого будут смещены вправо, в сторону увеличенных объемов, кроме одной точки, совпадающей с началом координат для кривой q(V) при ε=1 (рис. 4). В каждом из этих семейств и любых других, кривые q(V) при значениях ε, близких к единице и к нулю, не имеют практического значения.

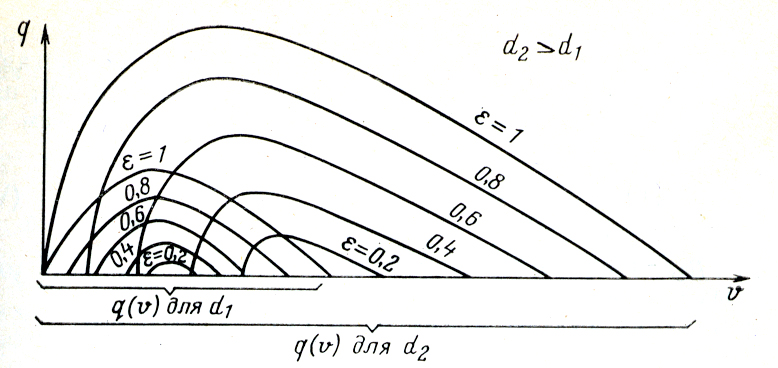
Рисунок 4. Семейство кривых q(V) для двух газожидкостных

подъемников различных диаметров

Определим к.п.д. процесса движения ГЖС. На каждой кривой q(V) имеется еще одна характерная и очень важная точка, точка так называемой оптимальной производительности, соответствующая наибольшему к.п.д.

Если проанализировать произвольную кривую q(V), для которой ε=const, то для нее будут следующие рассуждения.

Из определения понятия к.п.д. η следует, что

. (2)

Полезная работа заключается в поднятии жидкости с расходом на высоту , так что

. (3)

Затраченная работа - это работа газа, расход которого, приведенный к стандартным условиям, равен . Полагая для простоты, что процесс расширения газа изотермический, на основании законов термодинамики идеальных газов можем записать

, (4)

где - абсолютное давление у башмака; - абсолютное давление на устье, - атмосферное давление.

Подставляя (3) и (4) в (2), получим

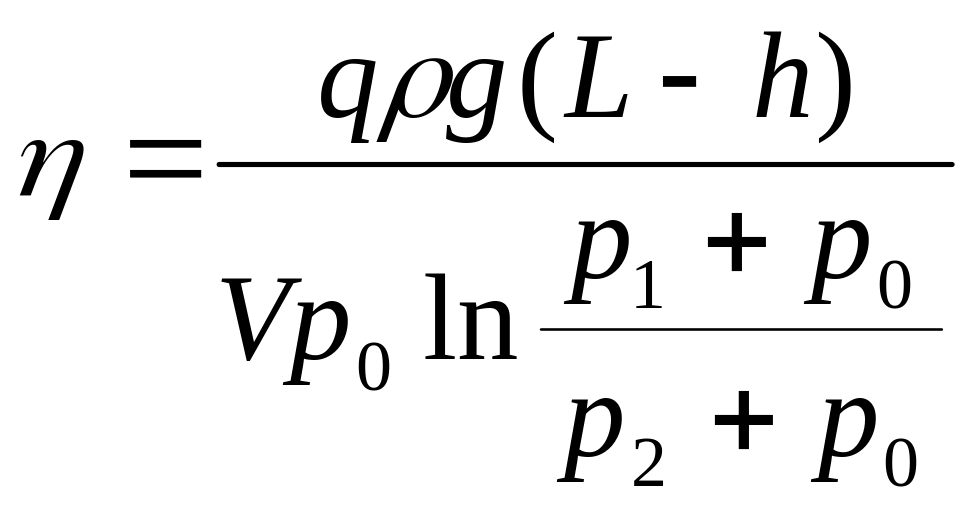. (5)

В (5) все величины, кроме и , постоянны, так как рассматривается одна кривая , для которой . Следовательно, для данной кривой

, (6)

где С – константа.

Поэтому к.п.д. имеет максимальное значение в той точке, в которой отношение q/V максимально. Но q/V=tgφ, так как q – ордината, V – абсцисса, φ – угол наклона прямой, проведенная из начала координат через данную точку (q, V). Только для касательной tgφ будет иметь максимальное значение, так как только для нее угол φ максимален. Поэтому в точке касания прямой, проведенной из начала координат с кривой q(V), получают такой дебит q и такой расход газа V, для которых к.п.д. процесса будет наибольшим. Расход q при максимальном к.п.д. называют оптимальным дебитом q_опт.

Таким образом, для любой кривой q(V), имеющей , оптимальный расход жидкости определяется как точка касания касательной, приведенной из начала координат.

Удельным расходом газа называют отношение

. (7)

Из определения следует, что для точек начала и срыва подачи, когда q=0, а V>0, удельный расход R обращается в бесконечность. Для режима оптимальной подачи, когда к.п.д. имеет максимальное значение, R имеет минимальное значение. При максимальном к.п.д. должно расходоваться минимально возможное количество газа на подъем единицы объема жидкости. При режиме максимальной подачи q_max к.п.д меньше максимального η < η_max . Поэтому и удельный расход газа R будет при этом режиме больше оптимального. Величина R может быть получена для любой точки кривой q(V) путем деления абсциссы на ординату данной точки (рис. 5).

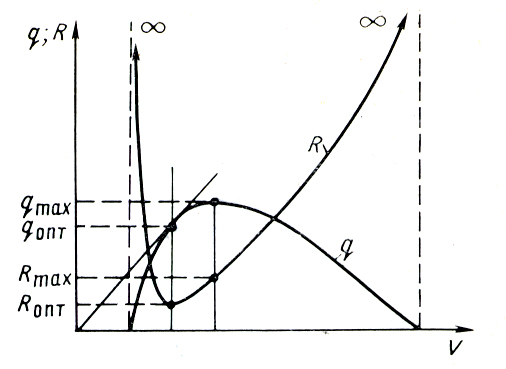
Рисунок 5. Зависимость удельного расхода газа R от общего

расхода газа V для данной кривой q(V)

Зависимость оптимальной и максимальной подач от относительного погружения

Для любого семейства кривых q(V), построенного для данного диаметра труб, можно найти q_max и q_опт и проследить их зависимость от изменения относительного погружения ε.

С увеличением ε величины q_max также увеличиваются по криволинейному закону (рис. 3 и 4). Оптимальные подачи q_опт , во-первых, всегда остаются меньше соответствующих q_max и, во-вторых, сначала увеличиваются с ростом ε, а затем при 0,5 < ε < 1 начинают уменьшаться. В частности, при ε = 1 кривая q(V) выходит из начала координат. Поэтому касательная, проведенная из начала координат, будет иметь точку соприкосновения с кривой q(V) в начале координат. Это означает для q(V) при ε = 1 q_опт = 0. Таким образом, величины q_опт должны сначала увеличиваться, затем уменьшаться и при ε = 1 обращаться в нуль. Наибольшая величина q_опт достигается при ε ≈ 0,5 – 0,6 (рис. 6). Это подтверждается многочисленными опытами различных исследователей. Отсюда следует важный для практики вывод: для достижения наибольшей эффективности работы газожидкостного подъемника необходимо осуществить погружение подъемной трубы под уровень жидкости на 50-60% от всей длины трубы L. Однако эта рекомендация в реальных условиях не всегда может быть выполнена из-за низкого динамического уровня или из-за ограниченного давления газа, используемого для этой цели.

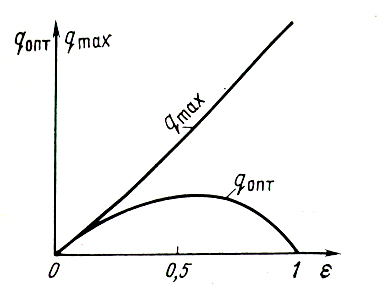
Рисунок 6. Зависимость оптимальной q_опт и максимальной q_max подачи

от относительного погружения ε

Структура потока ГЖС в вертикальной трубе

В зависимости от физических свойств жидкости и характера ввода газа в поток могут возникать различные структуры движения ГЖС в трубе, которые существенным образом влияют на энергетические показатели подъема жидкости. В фонтанных скважинах на участке НКТ, где давление меньше давления насыщения, выделяющийся из нефти свободный газ образует тонкодисперсную структуру, называемую эмульсионной. Мелкие газовые пузырьки более или менее равномерно пронизывают массу нефти, образуя практически однородную квазигомогенную смесь газа и жидкости. Вследствие своей малости (доли мм) и большой плотности газовые пузырьки обладают малой архимедовой силой. Поэтому их скорость всплытия относительно жидкости пренебрежимо мала и в расчетах может не учитываться. Это происходит до тех пор, пока в результате уменьшения давления при движении смеси вверх по трубе газовые пузырьки, расширяясь, увеличивают объемное газосодержание потока до 20-25%. При дальнейшем уменьшении давления и поступлении из нефти новых количеств газа пузырьки, сливаясь, образуют шарообразные формы (глобулы) больших размеров, измеряемые в диаметре несколькими сантиметрами. Скорость всплытия таких глобул в результате действия таких глобул в результате действия архимедовой силы становится большой, достигая нескольких десятков сантиметров в секунду. Это ухудшает энергетические показатели процесса подъема. Такая структура называется четочной.

При больших расходах газа возникает стержневая структура, при которой газ с распыленными в нем каплями жидкости движется непрерывным потоком, увлекая за собой по стенкам трубы волнистую пленку жидкости. При стержневой структуре движения скорость газа по отношению к жидкости достигает нескольких метров в секунду.

Между эмульсионной, четочной и стержневой структурами не существует резких границ перехода, на возникновение той или иной структуры существенной влияние оказывает вязкость нефти, а также наличие в ней различных ПАВ, способствующих диспергации (измельчению) газа в потоке (рис. 7).

Рисунок 7. Структуры газожидкостного потока:

а – эмульсионная; б – четочная, в – стержневая

Осн.: 1. [220-227], 3. [270-314]

Контрольные вопросы:

1. Как изменяется подача газожидкостного подъемника от расхода газа??

2. Какова зависимость положения кривых q(V) от погружения?

3. Какова зависимость положения кривых q(V) от диаметра трубы?

4. К.п.д. процесса движения ГЖС?