1 Билет.
Сұйықтар. Беттік керілу. Беттік керілу коэффициенті. Лаплас формуласы. Капиллярлық құбылыстар.
Сұйық
деп – көлемін өзгертпейтін, механикалық
әсерлесулердің тарапынан пішінін тез
өзгертуге бейім заттың агрегаттық
күйінің бір түрін айтады. Фаза
деп шекаралық бетпен бөлінген, барлық
нүктелерде физикалық қасиеттері бірдей
жүйе бөлігі айтылады.
Беттік
керілу —
екі фазаның(дененің)
бөліну бетінің термодинамикалық
сипаттамасы. Өлшем бірліктері Дж/м2 немесе
Н/м. Беттік керілуді бөліну беті сұйықтық
болған жағдайда, бет контурының ұзындық
бірлігіне әсер ететін және фазалардың
берілген көлемдерінде бетті ең кіші
шамаға (минимумға)
дейін жиыруға ұмтылатын күш ретінде де
қарастыруға болады. Екі қоюланған
(конденсацияланған) фазаның шекарасындағы
беттік керілу, әдетте, фазааралық
керілу деп
аталады.
Сұйықтың
табиғатына қарай анықталатын
пропорционалдық коэффициент σ
– беттік
керілу коэффициенті
д.а. Ол сан мәні жағынан бір өлшем
ұзындыққа сәйкес келетін беттің керілу
күшіне тең, яғни 
қабыршақтың ауданын бірлік өлшемге
кемітуге жұмсалатын жұмыс. σ=ΔA/ΔS.
Процесс
тұрақты температурада жүреді, сондықтан
беттің керілу коэффициенті өзгермейді,
ал қабыршақты созатын сыртқы күштің
жасаған жұмысы ΔA
оның потенциалдық энергиясын ΔE-ге
арттырады, яғни ΔE=-ΔA
,
бұл энергия
сұйықтың еркін бетінің энергиясы
деп аталады, сонда σ=ΔE/ΔS.
Бұл
сұйықтықтың беттік керілу коэффициенті,
бірлік ауданына келетін еркін
бет энергиясы деп
анықталады.
Қысым
бір дене екінші дене бетіне (мысалы,
ғимарат іргетасының грунтқа, сұйықтықтың
ыдыс қабырғасына,газдың піспекке, т.б.)
әсер еткенде пайда болатын қалыпты
күштің (дене бетіне перпендикуляр)
қарқындылығын сипаттайтын физикалық
шама.
Капиллярлық
құбылыстар–
бір-бірімен араласпайтын заттардың
шекарасында, беттік керілудің әсерінен
пайда болатын физикалық құбылыстар.Капиллярлық
қысым— судың
капиллярлық көтерілу биіктігіне
сәйкес келетін қысым.
Мұндай қысым жайында заңдылықты теория
жүзінде алғаш дәлелдеген белгілі француз
ғалымы П. Лаплас (1806 жылы).
Мұнда
p – сұйықтықтың сығылған бетіндегі
қысым , σ
– беттік керілу, 
-
сұйық бетінің ағысына перпендикуляр
екі қисықтың радиусы
Лаплас түрлендіруі — “оригинал” деп аталатын түрлендіру. Лаплас түрлендіруі операциялық есептеулерде, автоматты реттеуіштерге байланысты есептерді шешкенде жиі қолданылады. Электротехника, гидродинамика, жылу өткізгіштік, механика есептерінің бірқатары Лаплас түрлендіруі қолданалатын әдістер арқылы шешіледі.
2 Билет.
Нақты газдар. Ван-дер-Ваальс теңдеуі. Ван-дер-Ваальс изотермалары. Эндрюстің эксперименттік изотермалары. Газ-сұйық фазалық ауысуы
Нақты газдар
Нақты газдар.Газдың тығыздығы артқан сайын оның қасиеттері идеал газ күйінен ауытқи бастайды. Бұл жағдайда соқтығысулардың рөлі артып, молекулалардың мөлшерлері мен олардың өзара әсерлерін ескермеуге болмай қалады. Мұндай газды нақты (реал) газ деп атайды. Бойл-Мариот және Гей-Люссак заңдарына бағынбайтын газдар. Газдардың мінсіз жағдайдан ауытқу мөлшері олардың тығыздығы артқан сайын (қысым жоғары,температура төмен) өсе түседі, яғни газ тамшылары неғұрлым бір-біріне жақын орналасқан сайын, олардың бір-біріне әсері солғұрлым күшейе түседі. Идеал газ қасиетінен нақты газдың ауытқуы-молекулалардың өлшемі мен әсерлесуін ескеру керек екенін білдіреді. Осыларды ескеріп 1873 жылы нақты газдың күй теңдеуін голландиялық физик Ван-дер-Ваальс алған.
1моль
газ үшін Ван-дер-Ваальс
теңдеуі
мынадай:
a,b тұрақты шамалар,мәндері әртүрлі газдар үшін тәжірибеден алынады.
молекулалар
арасындағы өзара тартылыс күштерінің
әсерін ескереді ж/е ол ішкі
қысым д.а.
b- тебілу күштерін ескереді,яғни молекулалардың көлемін ескереді.
Ван-дер-Ваальстың теңдеуін жақшаларын ашып, қарапайым түрлендіруден кейін мына түрге келтіруге болады:
Екі жағын p-ға бөліп, бұл теңдеуді былай жазамыз:
V көлемге қатысты осы теңдеу үшінші дәрежелі, сондықтан оның 3 түбірі болады: 3 нақты немесе 1 нақты екі жорамал түбірі бар. Демек бір қысымның мәніне көлемнің әр түрлі 3 мәні сәкес келеді. Ван-дер-Ваальс теңдеуінің түбірлерінің мағынасын ашу үшін
бойынша изотермдерін,яғни тұрақты температурада қысымның көлемге қатысты тәуелділігін талдау қажет, онда
мына түрде жазу қолайлы:
Осы теңдеу бойынша теориялық изотермнің минимумдары, максимумдары бар, V=b болғанда, p=∞ екенін байқаймыз.Сондықтан V-көлем b-дан кем болуы мүмкін емес олай болса газ орналасқан ыдыстың көлемі барлық молекулалардың төрт еселенген көлемінен болуы мүмкін емес Ван-дер Ваальс теңдеуі б-ша СО2 үшін әртүрлі есептелген теориалық суретте көрсетілген .
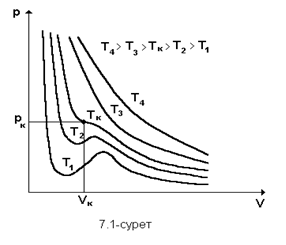
Ван-дер Ваальс изотерімдердің түрі идеал газдікіндей гипербола болмайтыны осы графиктен айқын көрінеді. Температура өскен сайын суреттегі теориялық изотермдердің ерекше толқын тәріздес иіліс бөлімі кішірейіп, Т=Тк деп белгіленген изотермнің нүктесінде жойылады. Осы Тк температурасы критикалық температура д.а.
Газ-сұйық фазалық ауысуы
Заттың бірқатар физикалық қасиеттерінің бір-біріне ауысуын секірмелі түрде өтуі , мысалы судың буға айналуы н-cе будың суға айналуы, мұздың еруі заттың агрегаттық күйлері д.а.
Ван-дер-Ваальстың изотермдерің Максвелдің тандауы б-ша fedf және dcbd аудандары бірдей болатындай, bdf түзу сызығы бойымен зат f күйден b күйге өтеді. Онда зат бір фазалық fedcb қыйсығымен, әлде екі фазалық bdf түзуімен өтеме істелінетін жұмыс бірдей. Сурет онда fedcb қыйсығымен шектелетін аудан bdf түзуінің астындағы ауданға тең болады. Сондықтаң fedcb қыйсығының өркештерінің аудандары тең болады.
Ван-дер-Ваальс теңдеуі заттың екі фазасын: газ тәріздес (ab бөлігі) және сұйық (fg бөлігі ) бейнеленгенімен одан түзу сызықты bdf бөлігінің орны аңықталмайды.
Ван-дер-Ваальс теңдеуін тәжірибе арқылы тексергенде, оның нақты газдардың p,v,t параметірлер арасындағы қатынастар жуықтап қана суреттейтіні көрінді. Теңдеудің a ж.е b тұрақтылары да температурақа тәуелді болып шықты. Сол себептен Ван-дер-Ваальс теңдеуі нақты газ күйін жуықтап қана бейнелейді. Ван-дер-Ваальс теңдеуінен тікелей шығатың өте маңызды мәселе-заттың критикалық температурасы мен критикалық күйінің болуы.