Дистанционная школа обществознания

Код курса: Э 1

9 - 10 классы

Модуль 2. Рыночное равновесие

— Послушайте, Вы интересуетесь политикой? Я на днях прочел в газете, что приняли один закон, его еще называют закон спроса и предложения.

Я, как мог, постарался ему втолковать, что речь идет не о законодательном акте, а о законе политической экономии.

— Вот оно как, — сказал Финч. — Я об этом законе много чего слышал года два тому назад, но все больше с одного боку.

— Верно, — подтвердил я. — У ораторов этот закон не сходит с языка. Похоже, они жить без него не могут.

О’Генри. Спрос и предложение.

2.1 Спрос

Ключевые понятия:

Спрос. Шкала спроса. Кривая спроса. Закон спроса. Индивидуальный и рыночный спрос.

Эластичность, коэффициент эластичности. Точечная и дуговая эластичность. Эластичность спроса по цене.

Предполагается, что после изучения этого раздела

учащиеся будут знать: понятия «спрос», «индивидуальный спрос», «рыночный спрос», «эластичность спроса по цене»; закон спроса; факторы, влияющие на спрос.

учащиеся будут уметь: читать и строить шкалу и график спроса на условных примерах; различать изменение величины спроса и сдвиг кривой спроса; изображать сдвиги кривой спроса; строить кривую рыночного спроса на основании данных об индивидуальном спросе; приводить примеры эластичного и неэластичного спроса; вычислять коэффициенты дуговой и точечной эластичности спроса по цене; определять эластичность спроса по цене на основании изменения общей выручки.

2.1.1 Индивидуальный и рыночный спрос.

Спрос – это желание и возможность купить данный товар.

Изобразим множество возможностей в виде овала. Отметим К – возможность купить калоши, которые мне не нужны.

Изобразим множество желаний в виде овала. Отметим М – желание купить розовый мерседес последней модели, на который у меня нет денег.

А теперь закрасим пересечение этих множеств и отметим А – возможность купить апельсины, которые мне нужны или желание купить апельсины, на покупку которых у меня хватает денег. Закрашенная общая часть множеств желаний и возможностей показывает спрос.

Индивидуальный спрос – это спрос одного покупателя на один товар. Для того чтобы задать индивидуальный спрос, необходимо описать, какое количество товара покупатель готов купить в течение определенного периода времени (день, месяц и т.п.) по всем возможным ценам на этот товар. Назовем количество товара, которое покупатель готов купить по какой-то конкретной цене – величиной или объемом спроса.

Функция индивидуального спроса – это зависимость величины индивидуального спроса от разных факторов: цены данного товара, выделенной на покупки суммы, моды, погоды,

предпочтений, цен на другие товары и т.д. Отследить одновременно влияние всех факторов невозможно, воздействие их может быть разной силы, они могут действовать в противоположных направлениях, нейтрализуя воздействие друг друга и т.д. В таких случаях ученые применяют принцип ceteris paribus – при прочих равных. Например, физики рассматривают движение без трения, в вакууме, а экономисты – при неизменных неценовых факторах. Зафиксировав неценовые факторы, получим функцию от одного переменного - функцию индивидуального спроса от цены.

Функцию спроса можно задать в виде таблицы:

Цена товара, ден.ед.	5	10	15	20	25
Величина спроса, штук	60	50	40	30	20

в виде уравнения: Q_d = 70 – 2P, где Q_d – величина спроса, Р – цена товара;

в виде графика:

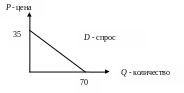
Учителю. Обычно независимую переменную (причину) откладываем по горизонтальной оси, а зависимую (следствие) – по вертикальной. Обратите внимание на то, что независимая переменная Р, а зависимая - Q .

И оси мы направили не так, как это сделали бы математики, но так принято.

Все три способа теоретически являются взаимозаменяемыми, так как, имея таблицу, можно построить график и вывести уравнение, имея уравнение, можно задать таблицу и построить график и т.д.

Между ценой данного товара и величиной спроса на него существует обратная зависимость: при прочих равных условиях (неизменный доход, неизменные цены на другие товары, предпочтения потребителя и пр.) чем выше цена, тем меньше величина спроса. И наоборот: чем ниже цена, тем больше величина спроса. Эта зависимость называется законом спроса.

Закон спроса объясняется действием эффекта дохода и эффекта замены.

Эффект дохода возникает из-за изменения реального дохода потребителя вследствие ограниченности его дохода. Пусть, например, на покупку выделено100 рублей. Тогда при цене товара 10 рублей можно купить 10 единиц товара. Но если цена возрастет до 20 рублей, то можно купить только 5 единиц товара, т.е. реально потребитель стал беднее.

Э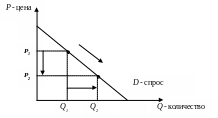 ффект замены возникает при росте цены из-за переключения на другие относительно подешевевшие товары-заменители. Если цена товара возрастет при прочих равных условиях, то данный товар подорожает относительно других товаров. Соответственно, товары-заменители подешевеют относительно данного товара. В этом случае потребитель может частично или полностью заменить данный товар другими товарами в своей потребительской корзине.

Таким образом, изменение цены товара приводит к изменению величины спроса на товар, что означает на графике движение вдоль кривой спроса.

Рыночный спрос – это суммарный спрос на товар всех потребителей при любой возможной цене товара в течение определенного периода времени.

Если известны индивидуальные функции спроса, то рыночный спрос можно получить аналитически, а также графически, путем суммирования индивидуальных спросов при любой возможной рыночной цене (суммирование по горизонтали, по оси Q).

Задача 1.

По цене 20 рублей мама купит 5 кг картофеля, а по цене 30 рублей только 3 килограмма. Найдите функцию спроса и постройте график, считая, что спрос мамы на картофель линейный.

Решение.

Занесем известные данные о спросе в таблицу:

P, цена в рублях	20	30
Qd, величина спроса ( кг)	5	3

Линейная функция спроса в общем виде выглядит так: Q_d = а - b∙Р,

где Q_d – величина спроса, Р – цена, а и b – положительные числа.

Для того чтобы найти функцию спроса мамы на картофель, необходимо найти значения а и b. Подставим имеющиеся значения цены и величины спроса в формулу, получим два уравнения. Составим и решим систему из двух уравнений с двумя неизвестными.

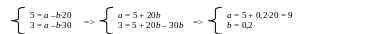
Таким образом, функция спроса мамы на картофель имеет вид: Q_d = 9 – 0,2∙Р.

Графиком спроса мамы на картофель будет прямая, т.к. зависимость линейная. Чтобы изобразить эту прямую, достаточно найти две точки.

Q_d = 9 при Р = 0. То есть максимальное количество картофеля, которое мама готова купить, 9 кг. Отметим это точкой на оси Q.

Q_d = 0 при Р = 45 (0 = 9 – 0,2Р; 0,2Р = 9; Р = 9/0,2 = 45).

То есть максимальная цена, выше которой мама не готова платить, 45 рублей.

Отметим точку на оси Р.

P, цена в рублях	45	0
Qd, величина спроса в кг	0	9

Обозначим на графике полученные крайние точки и соединим их отрезком.

О чевидно, что точки (5; 20) и (3;30) также лежат на этом графике.

Конечно, график можно было построить, отметив две заданные в задаче точки. Но уметь находить точки пересечения с осями – важный навык.

Ответ: Q_d = 9 – 0,2∙Р.

Задача 2.

АЗС «Ромашка» находится между деревнями Ельцовка и Сосновка. Недельный спрос жителей Ельцовки на бензин марки АИ92 задан уравнением Q_d1 = 2400 – 60∙Р, а недельный спрос жителей Сосновки на тот же бензин задан уравнением Q_d2 = 2000 – 40∙Р, где Р – цена бензина в рублях, Q_d1 – величина спроса на бензин жителей Ельцовки (в литрах), Q_d2 – величина спроса на бензин жителей Сосновки (в литрах). Постройте кривые спроса на бензин Ельцовки и Сосновки. Найдите суммарный спрос на бензин АЗС «Ромашка» жителей двух деревень. Решение представьте аналитически и графически.

Решение.

Так как функции спроса вида Q_d = а - b∙Р, значит, линейные, и для построения графика каждой достаточно найти координаты двух точек. Пусть это будут крайние точки – точки пересечения кривой спроса с осями Р и Q.

Строим кривую спроса Ельцовки. Q_d1 = 2400 при Р = 0. Найдем цену, при которой Q_d1 = 0.

0 = 2400 – 60∙Р; 60Р = 2400; Р = 2400/60 = 40.

Занесем данные в таблицу:

P, цена в рублях	0	40
Qd1, величина спроса в литрах	2400	0

Отметим эти точки на графике и построим кривую спроса:

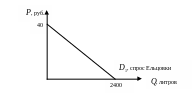
Строим кривую спроса Сосновки. Q_d2 = 2000, при Р = 0. Найдем цену, при которой Q_d2 = 0.

0 = 2000 – 40∙Р; 40Р = 2000, Р = 2000/40 = 50.

Занесем данные в таблицу:

P, цена в рублях	0	50
Qd2, величина спроса в литрах	2000	0

Отметим эти точки на графике и построим кривую спроса:

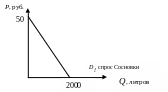
Найдем суммарный спрос. Для этого необходимо рассмотреть два интервала цен: от 40 до 50 рублей и от 0 до 40 рублей.

Если цена на бензин будет от 40 до 50 рублей, то жители Ельцовки не будут покупать бензин на АЗС «Ромашка» (при Р выше 40 Q_d1 = 0). Значит, в данном интервале цен спрос на бензин будут предъявлять только жители Сосновки.

По цене 50 рублей Q_d2 = 0, а по цене 40 рублей Q_d2 = 2000 - 40∙40 = 400 (литров).

В интервале цен от 0 до 40 рублей спрос на бензин будут предъявлять жители обеих деревень.

При Р = 0 Q_d1+d2 = 2400 + 2000 = 4400 (литров), а при Р = 40 Q_d1+d2 = 0 + 400= 400.

Занесем эти данные в таблицу:

P, цена в рублях	50	40	0
Qd1+d2, величина спроса в литрах	0	400	4400

О тметим полученные точки и соединим их отрезками.

Проверим по графику любую ситуацию, например, при Р=10

Q_d1+d2 = Q_d1 + Q_d2 = (2400 – 60∙10) + (2000 – 40∙10) = 1800 + 1600 = 3400.

Уравнение верхнего участка графика – это уравнение спроса Сосновки.

Уравнение на суммарном участке находится путем сложения правых частей двух уравнений:

Q_d1+d2 = (2400 – 60Р) + (2000 – 40Р) = 4400 – 100Р.

Запишем теперь наше решение аналитически:

Обратите внимание на то, что график суммарного спроса выглядит мягче. Представьте, что надо построить суммарный спрос не двух покупателей, а трех – график будет состоять из трех отрезков. Семь покупателей – семь отрезков, и кусочно-линейный график уже зрительно не делится на отрезки. Остается сделать вывод о том, что график суммарного спроса многих покупателей в общем виде – гладкая кривая.

Величина спроса на товар зависит не только от цены товара, но и от неценовых факторов. Рассмотрим такие неценовые факторы спроса:

1. изменение вкусов и предпочтений потребителей;

2. изменение числа покупателей на рынке;

3. изменение цен на товары-заменители и на дополняющие товары;

4. изменение доходов покупателей;

5. изменение ожиданий покупателей относительно будущих доходов и цен.

Если изменится любой неценовой фактор, то изменится спрос и функция спроса на товар. На графике это выглядит как сдвиг кривой спроса. При увеличении спроса кривая спроса сдвинется вправо (вдоль оси Q), при уменьшении спроса – влево.

Пример 1. Пусть спрос задан функцией: Q_d1 = 100 – 2P (функция спроса - линейная). Известно, что изменение вкусов повлекло за собой изменение спроса: количество уменьшилось на 30 при каждой цене. Покажем в таблице изменение спроса на товар

Цена товара, руб.	5	10	15	20	25
Старая величина спроса, штук	90	80	70	60	50
Новая величина спроса, штук	60	50	40	30	20

Нужно ли перебирать так много точек? Нет, если функция линейная, достаточно

двух точек. Какие точки лучше? точки пересечения с осями.

Используя данные таблицы, получим новое уравнение спроса: Q_d2 = 70 – 2P.

Н а рисунке видим сдвиг влево.

Поскольку величина спроса уменьшилась на 30 единиц по каждой цене, новое уравнение спроса получается из старого вычитанием: Q_d2 = Q_d1 - 30 = (100 – 2Р) - 30 = 70 – 2Р.

Пример 2. Пусть спрос задан функцией: Q_d1 = 100 – 2P (функция спроса - линейная). Известно, что изменение вкусов повлекло за собой изменение спроса: количество уменьшилось в 2 раза при каждой цене. Покажем в таблице изменение спроса на товар.

Цена товара, руб.	0	5	10	15	20	25	50
Старая величина спроса, штук	100	90	80	70	60	50	0
Новая величина спроса, штук	50	45	40	35	30	25	0

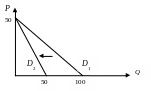
Учителю: добавим значения в крайних точках. Увидим, что этих точек было достаточно для вычислений.

Используя данные таблицы, получим новое уравнение спроса: Q_d2 = 50 – P.

График спроса поворачивается по часовой стрелке вокруг точки пересечения графика с вертикальной осью.

Задача 3.

С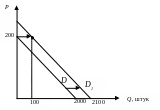 редние школы города N получили дополнительное финансирование на развитие своей материальной базы. В результате величина спроса школ города N на интерактивные доски увеличилась на 100 единиц при каждой цене. Покажите изменение графически. Найдите уравнение спроса школ на интерактивные доски после получения дополнительного финансирования, если первоначально спрос выглядел как Q_d = 2000 – 10Р, где Р – цена в тыс. рублей, Q_d – количество, в штуках.

Решение.

Построим график первоначального спроса.

Для этого найдем точки пересечения кривой спроса с осями Р и Q.

Q = 2000 при Р = 0.

Q = 0 при Р = 200.

Теперь отметим эти точки на графике.

Заметим, что спрос существовал в диапазоне цен от 0 до 200 тыс. рублей.

Поскольку величина спроса увеличилась на 100 единиц по каждой цене, новое уравнение спроса будет выглядеть как

Q_d1 = Q_d + 100 = (2000 – 10Р) + 100 = 2100 – 10Р. На рисунке это изменение отразится в сдвиге линии спроса на 100 единиц вправо (вдоль оси Q).

График переместился вправо, т.к. изменился доход покупателя (школы получили дополнительное финансирование);

мы не обсуждаем, по какой цене будет куплен товар, изменилась готовность покупать.

Ответ: Q_d1 = 2100 – 10Р.

Обратите внимание на то, что самый легкий (удачный для решения задач) случай, когда табличные данные соответствуют линейной зависимости, и мы можем увидеть все три способа задания одной и той же функции. Такое возможно не всегда. Если в таблице только две пары чисел, то это не значит, что функция спроса линейная. Это значит, что мы располагаем такой - ограниченной! – информацией.

Предложенные ниже задачи 4 и 5 не позволят выработаться такому стереотипу. Их особенность:

вместо «каждой данной цене соответствует своя величина спроса»

мы видим «каждому данному диапазону цен соответствует своя величина спроса».

Задача 4.

Дима и Слава решили перекусить после уроков. У Димы нашлось в кармане 70 рублей, а у Славы – 110 рублей. Чтобы почувствовать себя сытым, Диме нужно съесть три гамбургера, а Славе достаточно двух. Постройте кривые спроса Димы и Славы на гамбургеры, если каждый из них купит еще по стакану сока за 10 рублей.

Решение.

Всего Дима готов потратить на гамбургеры 60 рублей (так как 10 рублей нужно оставить на сок). Если гамбургер будет стоить 60 рублей, Дима сможет купить 1 штуку, чтобы он смог купить 2 гамбургера, цена должна быть не больше 30 рублей. Но если цена будет не выше 20 рублей, то Дима сможет купить 3 гамбургера, а больше ему и не нужно. Занесем эти данные в таблицу.

Шкала спроса Димы на гамбургеры

Интервал цен, заданный словесно	дешевле 20	от 20 до 30	от 30 до 60	дороже 60
или математически	[0;20]	(20;30]	(30;60]	(60;∞)
Величина спроса Димы на гамбургеры	3 штуки	2 штуки	1 штука	0 штук

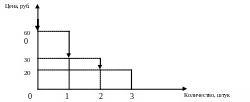И зобразим эти данные графически. Так как количество товара измеряется целыми единицами, то график спроса будет кусочно-линейным. Так, например, если цена на гамбургер будет 55 рублей, то Дима все равно купит только 1 гамбургер и у него останется еще 5 рублей.

Построим шкалу спроса для Славы. Всего он может потратить на гамбургеры 100 рублей (10 рублей оставляем на стакан сока). Если цена на гамбургеры будет выше 100 рублей, то Слава не сможет купить ни одного гамбургера. Если же цена будет 50 рублей и ниже, то Слава сможет купить два гамбургера, а больше ему и не надо.

Шкала спроса Славы на гамбургеры

Интервал цен	[0;50]	(50;100]	(100;∞)
Величина спроса Славы на гамбургеры	2 штуки	1 штука	0 штук

И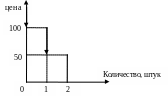 зобразим эти данные графически. График спроса Славы на гамбургеры будет также кусочно-линейным.

Задача 5.

Используя данные задачи 4, опишите суммарный спрос Димы и Славы на гамбургеры в виде шкалы спроса и графика спроса.

Решение.

Для того чтобы описать суммарный спрос двух покупателей, нам необходимо суммировать величины спроса Димы и Славы по всем возможным ценам. Сравним диапазоны цен у покупателей, заметим, что они разные, и учтем границы индивидуальных диапазонов.

Если цена гамбургера окажется в интервале цен от 0 до 20 рублей, то Дима купит 3 гамбургера, а Слава - 2, вместе они купят 5 штук.

Если цена будет выше 20, но не выше 30, то Дима купит 2 гамбургера и Слава купит 2, итого 4 штуки.

При цене выше 30, но не выше 50, Дима купит 1 гамбургер, и Слава купит 2 штуки, итого 3.

При цене выше 50, но не выше 60, Дима купит 1 гамбургер, и Слава купит 1, итого 2 штуки.

При цене от 60 до 100 Дима не сможет купить ничего, а Слава купит 1 гамбургер, итого 1 штука.

При цене выше 100 рублей оба подростка не смогут купить гамбургеры.

Шкала суммарного спроса Димы и Славы на гамбургеры:

Интервал цен, рублей	[0;20]	(20;30]	(30;50]	(50;60]	(60;100]	(100;∞)
Величина суммарного спроса на гамбургеры, штук	5	4	3	2	1	0

Изобразим теперь эти данные графически. График суммарного спроса на гамбургеры будет также кусочно-линейным.

О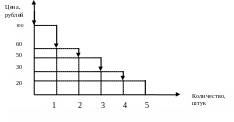 братите внимание то, что график суммарного спроса содержит больше отрезков, интервалы цен стали короче, вид у графика мягче, плавнее.

Задача 6.

Спрос первой группы покупателей задан уравнением Q₁ = 6 – P, спрос второй группы покупателей задан уравнением Q₂ = 3 – 1/3Р, где Q₁ и Q₂ – величина спроса на товар (в штуках), Р – цена (в денежных единицах). Какую цену должен назначить продавец, чтобы продать на рынке 5 единиц товара?

Решение.

Найдем рыночный спрос на товар. Первая группа покупателей готова платить только меньше 6 д.е. за штуку (при Р = 6, Q₁ = 0), а при Р = 0 готова приобрести 6 штук товара. Вторая группа покупателей готова платить только меньше 9 д.е. за штуку (при Р = 9, Q₂ = 0), а при Р = 0 готова приобрести 3 единицы товара. Таким образом, при цене от 0 до 6 рублей будут покупать обе группы, при цене выше 6, но не выше 9, будет покупать только вторая группа, а при цене выше 9 товар не купит никто. Изобразим ситуацию графически:

О пишем суммарный спрос двух групп покупателей:

Из графика видно, что 5 единиц товара можно продать только в интервале цен от 0 до 6. На этом интервале суммарный спрос описывается уравнением Q₍₁₊₂₎= 9 – 4/3Р. Подставим в это уравнение вместо Q₍₁₊₂₎ значение 5.

5 = 9 – 4/3Р, откуда Р = 3.

Можно обсудить, сколько купит каждая группа (в задаче это не спрашивается, однако послужит для проверки).

Подставим цену 3 в спрос первой группы Q₁ = 6 – 3 = 3; в спрос второй группы Q₂ = 3 – =2.

3 + 2 = 5 – купят две группы вместе.

Ответ: 3 д.е.