Основные свойства теплового излучения
Тепловое излучение происходит по всему спектру частот от нуля до бесконечности
Интенсивность теплового излучения неравномерна по частотам и имеет явно выраженный максимум при определенной частоте
C ростом температуры общая интенсивность теплового излучения возрастает
C ростом температуры максимум излучения смещается в сторону больших частот (меньших длин волн)
Тепловое излучение характерно для тел независимо от их агрегатного состояния
Отличительным свойством теплового излучения является равновесный характер излучения. Это значит, что если мы поместим тело в термоизолированный сосуд, то количество поглощаемой энергии всегда будет равно количеству испускаемой энергии.
Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:
Мощность излучения абсолютно чёрного тела прямо пропорциональна площади поверхности и четвёртой степени температуры тела:
|
где
-
степень черноты (для всех веществ
,
для абсолютно черного тела
).
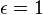Экзаменационный билет №30
Незатухающие гармонические колебания. Уравнение гармонических колебаний.
Колебания обычно если они незатухающие выражают гармоническим законом движения. y=A * sin( wt + a) Этот закон является решением линейного однородного дифференциального уравнения незатухающих гармонических колебаний: y'' + w * w * y =0 - собственно его вы и ищите. в этом уравнении y - координата , y'' - ускорение (2ая производная координаты по скорости) w - частота колебаний В случае когда в системе с незатухающими колебаниями есть внешнее периодическое возбуждение. То дифф уравнение имеет вид: y'' + w * w * y =f0 * sin(pt) f0 * sin(pt) - задает возбуждение, p - частота возбуждения. Общее решение этого уравнения - общее решения ду без внешнего возбуждения + частное решение этого уравнения
Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или
,
где х —
смещение (отклонение) колеблющейся
точки от положения равновесия в момент
времени t; А —
амплитуда колебаний, это величина,
определяющая максимальное отклонение
колеблющейся точки от положения
равновесия; ω —
циклическая частота, величина,
показывающая число полных колебаний
происходящих в течение 2π секунд;
—
полная фаза колебаний,
—
начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
Закон Джоуля – Ленца для постоянного тока.
Работа и мощность постоянного тока. Закон Джоуля-Ленца.
При прохождении тока в цепи электрическое поле совершает работу, которую называют работой тока. Для напряжения U между точками цепи следует формула работы электрического поля:
А = q ∙ U,
Где q – переносимый на этом участке заряд. При постоянном токе I переносимый за промежуток времени ∆t заряд q = I ∙∆ t и работа электрического тока определяется выражением
А = I∙ U∙∆t, = А∙ В ∙ с = Дж.
Работа тока на участке цепи равна произведению силы тока на напряжение на этом участке и на время, в течение которого совершалась работа.
По закону Ома I = U / R и, следовательно, работу тока для однородного участка цепи можно рассчитывать любым эквивалентным способом
А = I∙ U∙∆t = I2 ∙ R∙ ∆t = (U2 / R) ∙ ∆t
Мощность электрического тока равна работе, которая совершается током за единицу времени
P = A / ∆t = U∙I = I2 ∙ R= U2 / R.
В СИ мощность электрического тока измеряется в ваттах:
= 1 Дж/с = 1 А ∙В = 1 Вт.
Прохождение тока через проводник, обладающий сопротивлением, всегда сопровождается выделением теплоты. Количество теплоты, выделившегося за время ∆t, определяется законом Джоуля-Ленца:
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления и времени прохождения тока по проводнику
Q = I2 ∙ R∙ ∆t
Если на участке цепи не совершается механическая работа и ток не производит химического действия, то вся работа затрачивается на нагревание проводника
А = Q. Для однородного участка цепи выполняется закон Ома и поэтому
Q = A = I ∙ U ∙∆t = I2 ∙R ∙∆t = (U2 / R) ∙ ∆t
Из соотношений работы и энергии электрического тока вытекают следующие соотношения для единиц измерения:
1 Вт∙с = 1 Дж,
1 Вт = 1 В ∙ А,
1 Дж = 1 В∙ А ∙с.
Кроме единиц СИ, применяются несистемные единицы:
Для мощности 1 кВт = 1000 Вт;
Для энергии 1 Вт∙ ч = 3600 Дж = 3,6 ∙103 Дж,
1 кВ ч = 3600000Дж =3,6 ∙106 Дж.
Корпускулярно-волновой дуализм. Гипотеза де Бройля.
Французский ученый Луи де Бройль (1892–1987) в 1924 г. в докторской диссертации «Исследования по теории квантов» выдвинул смелую гипотезу об универсальности корпускулярно-волнового дуализма, утверждая, что поскольку свет ведет себя в одних случаях как волна, а в других – как частица, то и материальные частицы (электроны и др.) в силу общности законов природы должны обладать волновыми свойствами. «В оптике, – писал он, – в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не делалась ли в теории вещества обратная ошибка? Не думали ли мы слишком много о картине «частиц» и не пренебрегали ли чрезмерной картиной волн?» В то время гипотеза де Бройля выглядела безумной. Лишь в 1927 г., три года спустя, наука пережила огромное потрясение: физики К. Дэвиссон и Л. Джермер экспериментально подтвердили гипотезу де Бройля, получив дифракционную картину электронов.
Согласно квантовой теории света А. Эйнштейна, волновые характеристики фотонов света (частота колебаний v ф, релятивистской массой mф и импульсом рф) соотношениями:
По идее де Бройля, любая микрочастица, в том числе и с массой покоя ш0 Ц 0, должна обладать не только корпускулярными, но и волновыми свойствами. Соответствующие частота v и длина волны л определяются при этом соотношениями, подобными эйнштейновским:
Отсюда длина волны де Бройля —
Таким образом, соотношения Эйнштейна, полученные им при построении теории фотонов в результате гипотезы, выдвинутой де Бройлем, приобрели универсальный характер и стали одинаково применимыми как для анализа корпускулярных свойств света, так и при исследовании волновых свойств всех микрочастиц.