Экзаменационный билет №26

1. Кинетическая энергия вращающегося твёрдого тела.

Кинетическая энергия измеряется работой, которую тело может произвести благодаря инерции при затормаживании тела до полной остановки.

При вращательном движении роль массы m выполняет момент инерции I, а вместо линейной скорости v выступает угловая скорость ω, и формула кинетической энергии при вращательном движении тела вокруг неподвижной оси приобретает вид:

T_вр=Iω²/2

В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, кинетическая энергия складывается из энергии поступательного движения и энергии вращения:

T=(mv_c²+I_cω²)/2,

где m - масса катящегося тела; v_c - скорость центра масс тела; v_c - момент инерции тела относительно оси, проходящей через его центр масс; ω - угловая скорость тела.

2. Работа по перемещению проводника в электрическом поле.

Основные формулы

• Работа по перемещению замкнутого контура с током в маг­нитном поле

A=IDФ,

где  DФ — изменение магнитного потока, пронизывающего поверх­ность, ограниченную контуром; I — сила тока в контуре.

• Основной закон электромагнитной индукции (закон Фарадея — Максвелла)

где   — электродвижущая сила индукции; N — число витков кон­тура; Y — потокосцепление.

Частные случаи применения основного закона электромагнитной индукции:

а) разность потенциалов U на концах проводника длиной I, движущегося со скоростью u в однородном магнитном поле,

U=Blusina,

где a — угол между направлениями векторов скорости u и магнит­ной индукции В;

б) электродвижущая сила индукции , возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью со в однородном магнитном поле с индукцией В

где wt — мгновенное значение угла между вектором В и вектором нормали n к плоскости рамки.

• Количество электричества Q, протекающего в контуре,

где R — сопротивление контура; DY — изменение потокосцепления.

•Электродвижущая сила самоиндукции   возникающая в замкнутом контуре при изменении силы тока в нем,

где L — индуктивность контура.

• Потокосцепление контура Y=LI, где L — индуктивность контура.

• Индуктивность соленоида (тороида)

Во всех случаях вычисления индуктивности соленоида (тороида) с сердечником по приведенной формуле для определения магнит­ной проницаемости следует пользоваться графиком зависимости В от Н (см. рис. 24.1), а затем формулой

• Мгновенное значение силы тока I в цепи, обладающей актив­ным сопротивлением R и индуктивностью L:

а) после замыкания цепи

—ЭДС источника тока; t—время, прошедшее после замы­кания цепи;

б) после размыкания цепи

где l₀ — сила тока в цепи при t=0, t— время, прошедшее с момен­та размыкания цепи.

3) Дисперсия света

Дисперсией света называется зависимость показателя преломления п вещества от частоты v (длины волны..) света или зависимость фазовой скорости v световых волн от его частоты v. Дисперсия света представляется в виде зависимости n=f(..) Следствием дисперсии является разложение в спектр пучка белого света при прохождении его ч\з призму. Рассмотрим дисперсию света в призме. Пусть монохроматический пучок спета падает на призму с преломляющим углом А и показателем преломления п с преломляющим углом а. После двукратного преломления (на левой и правой гранях призмы) луч оказывается отклоненным от первоначального направления на угол ф. Из рисунки следует, что т. е. угол отклонения лучей призмой тем больше, чем больше преломляющий угол призмы. Из выражений вытекает, что угол отклонения лучей призмой зависит от величины n—1, а n — функция длины волны, поэтому лучи разных длин волн после прохождения призмы окажутся отклоненными на разные углы, т. е. пучок белого света за призмой разлагается в спектр, что и наблюдалось И. Ньютоном. Таким образом, с помощью призмы, так же как и с помощью дифракционной решетки, разлагая свет в спектр, можно определить его спектральный состав. Рассмотрим различия в дифракционном и призматическом спектрах. 1. Дифракционная решетка разлагает падающий свет непосредственно по длинам волн, поэтому по измеренным углам (по направлениям соответствующих максимумов) можно вычислить длину волны. Разложение света в спектр в призме происходит по значениям показателя преломления, поэтому для определения длины волны света надо знать зависимость n=f(..). 2. Составные цвета в дифракционном и призматическом спектрах располагаются различно. Следует, что в дифракционной решетке синус угла отклонения пропорционален длине волны. Следовательно, красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи в спектр по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны уменьшается. Поэтому красные лучи отклоняются призмой слабее, чем фиолетовые. называемая дисперсией вещества, показывает, как быстро изменяется показатель прело­мления с длиной волны.

Экзаменационный билет №27

1. Закон Бернулли для стационарного потока жидкости.

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Здесь

 — плотность жидкости,

 — скорость потока,

 — высота, на которой находится рассматриваемый элемент жидкости,

 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

 — ускорение свободного падения.

В научной литературе закон Бернулли, как правило, называется уравнением Бернулли^[1](не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли^[2][3] или интегралом Бернулли^[4][5].

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»^[6]).

Соотношение, близкое^[7] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Для горизонтальной трубы и уравнение Бернулли принимает вид:   .

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности :   .

Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

2. Сила Лоренца, действующая на движущуюся заряженную частицу во внешнем магнитном поле.

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Заряженная частица

Сила Лоренца f действующая на заряженную частицу (заряда q) при движении (со скоростью v). E поле и B поле меняются в пространстве и во времени.

Сила F, действующая на частицу с электрическим зарядом q, движущуюся со скоростью v, во внешнем электрическом E и магнитном B полях, такова:

где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:

где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J соответствует движению заряженного элемента dq в объеме dV .

Для непрерывного распределения заряда, сила Лоренца принимает вид:

где dF — сила, действующая на маленький элемент dq.

3. Поляризация света. Закон Малюса. где Io - интенсивность луча, прошедшего анализатор и поляризатор, когда их плоскости поляризации параллельны; I - интенсивность луча, выходящего из анализатора, без учета потерь в анализаторе в результате поглощения и рассеяния света.

Экзаменационный билет №28

1. Связь между угловой и линейной скоростями при вращении твёрдого тела вокруг неподвижной оси.

Угловая скорость и угловое ускорение Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 1). Ее положение через промежуток времени Δt зададим углом Δφ. Элементарные (бесконечно малые) повороты можно рассматривать как векторы (они обозначаются Δφ или dφ). Модуль вектора dφ равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т. е. подчиняется правилу правого винта (рис. 1). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определенных точек приложения: они могут откладываться из любой точки оси вращения. Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости ω=Т^-1, а ее единица — радиан в секунду (рад/с). Линейная скорость точки (см. рис. 1)

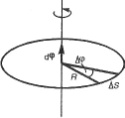
Рис.1 т.е v=ωR. В векторном виде формулу для линейной скорости можно написать как векторное произведение: При этом модуль векторного произведения, по определению, равен ωRsin(ω, R), а направление совпадает с направлением поступательного движения правого винта его вращения от ω к R.

Рис.2

Если ω=const, то вращение равномерное и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2π. Так как промежутку времени Δt=Т соответствует Δφ=2π, то ω=2π/T, откуда Т=2π/ω. Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения: n=1/T=ω/(2π), откуда ω=2πn. Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени:

Рис.3

При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему (рис. 4).

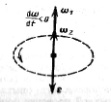
Рис.4 Тангенциальная составляющая ускорения a_τ=dv/dt , v=ωR и Нормальная составляющая ускорения Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а_τ, нормальное ускорение а_n) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами: s=Rφ, v=Rω, а_τ=Rε, a_n=ω²R. В случае равнопеременного движения точки по окружности (ω=const) ω=ω₀±εt, φ=ω₀t±εt²/2, где ω₀ — начальная угловая скорость.

2. Уравнение адиабатического процесса.

Термодинамика адиабатического процесса: dQ=0

Несмотря на то, что мы поочерёдно рассмотрели процессы с V=const, P=const, T=const, список характерных газовых процессов этим не исчерпывается. Обратим внимание, что при изохорическом процессе dA=0, при изотермическом процессе dU=0, и поэтому естественно рассмотреть процесс в котором dQ=0, т.е. адиабатический процесс. Адиабатический процесс - это процесс, протекающий без теплообмена с окружающей средой. Поскольку dQ = 0, то первое начало термодинамики примет вид: 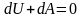- первое начало термодинамики при адиабатическом процессе. Такой вид первого начала термодинамики позволяет легко вычислить работу, совершаемую газом: 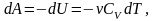или для конечного адиабатического процесса: - - работа, совершаемая газом при адиабатическом процессе. Исходя из dU + dA = 0, выведем закон, которому удовлетворяют параметры газа при адиабатическом процессе. 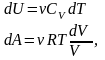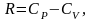Для этого dU и dA представим в виде Подставив это выражение в dU + dA = 0, получим дифференциальное уравнение: которое, разделив на С_V T и используя соотношения 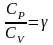, можно записать в виде . 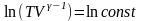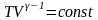Это дифференциальное уравнение приводится к полному дифференциалу: Решение этого дифференциального уравнения имеет вид или - уравнение адиабатического процесса в переменных(T,V). Воспользовавшись уравнением Менделеева-Клапейрона PV=RT, можно перейти к переменным (P,V) и (T,P). 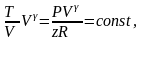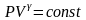Например, из Подставляя это в уравнение , получим или - уравнение Пуассона,

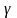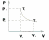
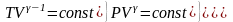где -коэффициент Пуассона. - уравнения адиабаты.

3. Правила смещения (α-, β-распады).

α – распад - характерен для ядер тяжёлых элементов. При α – распаде ядро атома испускает два протона и два нейтрона, связанные в ядро атома гелия. Их называют α – частицами, а такой вид радиоактивного превращения - α – распадом. Энергия α – частиц находится в пределах 1-10 МэВ. α – частица покидает ядро вследствие туннельного эффекта благодаря своим волновым св-вам β-распад – это процесс превращения в ядре атома протона → нейтрон или нейтрона → протон с выбросом Отдельные радиоактивные ядра испытывают распад независимо друг от друга, поэтому количество распавшихся ядер dN за время dt пропорционально числу имеющихся ядер N и времени-(1),где λ- постоянная распада, характерная величина для данного вещества. Знак минус указываот на убыль радиоактивных ядер. Из (1) находим уравнение (закон) радиоактивного распада ,где N₀-начальное количество ядер , N - количество нераспавщихся ядер к моменту времени t .      

Время, за которое распадается половина первоначального количества ядер, называется периодом полураспада Т_. Т.к. активность распада ядра носит случайный характер, то постоянная распада λ характеризует вероятность распада. Обратная же ей величина называется средним временем жизни радиоактивного ядра:

Радиоактивные вещества характеризуются активностью, равную числу ядер, распадающиеся за 1 с:  За единицу активности принят 1Бк (беккерелях) = 1распад/с. Часто пользуются внесистемной единицей I Кю (кюри) равно3,7*10¹⁰ расп/с. Активность радиоактивного вещества массой m равна где N_A — число Авогадро, А — атомная масса. Правила смещения для α и β-распадов:

^A_ZX-> ^A-4_Z-2Y+ ⁴₂α (Заряд ядра уменьшается на две единицы, а массовое число на 4.)

 ^A_ZX-> ^A_Z+1Y+ ⁰_-1e (Из материнского ядра образуется дочернее ядро, расположенное на одно место правее в табл Менд-ва).

Экзаменационный билет №29

1. Частота и период гармонических колебаний физического маятника. Приведенная длина физического маятника.