11 Преобразования плоскости

11.1 Основные определения

Определение 11.1. Фигура F^′ называется образом фигуры F при преобразовании f, если каждой точке фигуры F сопоставляется единственная точка фигуры F^′. Фигуру F называют прообразом фигуры F^′.

Определение 11.2. Если фигура F преобразуется в фигуру F ^′ преобразованием f , а затем фигура F ^′ преобразуется в фигуру F ^′′ преобразованием g, то преобразование фигуры F в фигуру F ^′′ называется композицией g ○ f .

Определение 11.3. Неподвижной точкой преобразования f называется такая точка A, что f (A) = A. Определение 11.4. Если f – взаимнооднозначное преобразование, то обратным к нему преобразова-

нием f⁻¹ будет такое преобразование, для которого f⁻¹(f(X)) = X для любой точки X. 102

11.2 Движения

Определение 11.5. Преобразование плоскости, которое сохраняет расстояние между точками, назы- вается движением плоскости.

Теорема 11.2.1 (свойства движений).

1. Движение обратимо. Преобразование, обратное движению, является движением. 
Доказательство. 
Докажем сначала, что движение обратимо, то есть "не склеивает"точки. Пусть X и Y – две раз- личные точки, образы которых при движении f совпадают, то есть f(X) = f(Y ). По определению движения ρ(f(X),f(Y )) = ρ(X,Y ). С одной стороны, ρ(X,Y ) ≠ 0, так как по условию X ≠ Y . C другой стороны, ρ(f (X ), f (Y )) = 0 в силу предположения. Полученное противоречие доказывает обратимость движения f. 
Докажем теперь, что преобразование обратное движению, является движением. Пусть f – задан- ное движение, f⁻¹ – обратное к нему преобразование, а X^′ и Y ^′ – две точки плоскости, являющи- еся образами точек X и Y . По определению обратного преобразования f⁻¹(X^′) = X,f⁻¹(Y ^′) = Y , при этом X^′ = f(X),Y ^′ = f(Y ) и X^′Y ^′ = XY . Следовательно, f⁻¹ – движение.

2. Три точки, лежащие на одной прямой, при движении переходят в три точки лежащие на одной прямой, и три точки, не лежащие на одной прямой, – в три точки не лежащие на одной прямой. 
Доказательство. 
Пусть движение переводит точки A,B,C в точки A^′,B^′,C^′. Тогда выполняются равенства 
A^′B^′ = AB, A^′C^′ = AC, B^′C^′ = BC. (1) 
Если точки A,B,C лежат на одной прямой, то одна из них, например точка B лежит между двумя другими. В этом случае AB + BC = AC, и из равенств (1) следует, что A^′B^′ + B^′C^′ = A^′C^′. А это равенство означает, что точка B^′ лежит между точками A^′ и C^′. Первое утверждение доказано. 
Теперь пусть точки A, B, C не лежат на одной прямой. По неравенство треугольника AB + BC > AC,AB+AC > BC,AC+BC > AB. Из этих неравенств следует, что A^′B^′+B^′C^′ > A^′C^′,A^′B^′+A^′C^′ > B^′C^′, A^′C^′ + B^′C^′ > A^′B^′. Из этих неравенств следует, что точки A^′, B^′, C^′ не лежат на одной прямой.

3. Отрезок движением переводится в отрезок. Движение сохраняет отношение «лежать меж- ду». 
Доказательство. 
Пусть концам отрезка AB движение f сопоставляет точки A^′ и B^′. Возьмём любую точку X отрезка AB. Тогда, AX +XB = AB, и, следовательно, A^′X^′ +X^′B^′ = A^′B^′. Тогда, точка X^′ = f(X) лежит между точками A^′ и B^′, то есть на отрезке A^′B^′. Далее, каждая точка Y ^′ отрезка A^′B^′ является образом некоторой точки Y отрезка AB, а именно той точки Y , которая удалена от точки A на расстояние A^′Y ^′. Следовательно, отрезок AB движением f переводится в отрезок A^′B^′. Кроме того, эти рассуждения доказывают, что если точка B лежит между точками A и C, то B^′ лежит между точками A^′ и C^′, то есть движение сохраняет отношение «лежать между».

4. При движении прямая в прямую, луч переходит в луч. Доказательство. 
Пусть A и B – произвольные точки данные прямой, A^′B^′ – прямая, проведенная через образы точек A и B при движении f. Рассмотрим произвольную точку C прямой AB. Точки A^′,B^′,C^′, где C^′ = f(C), лежат на одной прямой, то есть на прямой A^′B^′. Аналогично в силу того, что f⁻¹ – движение, для точки D^′ прямой A^′B^′ существует точка D прямой AB такая, что D^′ = f(D). Поскольку при движении взаимное расположение точек сохраняется, то луч при движении переходит в луч.

103

5. Треугольник движением переводится в треугольник. Доказательство. 
Три точки A,B,C, не лежащие на одной прямой, переходят при движении в точки A^′,B^′,C^′ соответственно, не лежащие на одной прямой. Кроме того отрезки AB,BC и AC переходят в отрезки A^′B^′,B^′C^′ и A^′C^′. Таким образом, треугольник ABC переходит в треугольник A^′B^′C^′. Причём A^′B^′ = AB,A^′C^′ = AC,B^′C^′ = BC. Тогда по третьему признаку равенства треугольни- ков _△ABC = _△A^′B^′C^′. Кроме того треугольник ABC заполняется отрезками, соединяющими вершину A с точками X противоположной стороны BC. Каждому отрезку AX это движение сопоставит отрезок A^′X^′, где точка X^′ лежит на отрезки B^′C^′. Все эти отрезки A^′X^′ заполнят треугольник A^′B^′C^′. Таким образом внутренность треугольника ABC переходит во внутренность треугольника A^′B^′C^′. 
Движение сохраняет величины углов. Рассмотрим три точки A,B,C, не лежащие на одной пря- мой. Она задают лучи AB и AC, являющиеся сторонами угла BAC. Пусть A^′,B^′,C^′ – соот- ветственно образы рассматриваемых точек A,B,C. Докажем, что _∠BAC = _∠B^′A^′C^′. Действи- тельно, так как треугольник A^′B^′C^′ является образом треугольника ABC, то эти треуголь- ники равны. Следовательно, и углы этих треугольников соответственно равны, в частности, _∠BAC = _∠B^′A^′C^′.

6. При движении сохраняются площади многоугольных фигур (произвольных фигур). Доказательство. 
Многоугольные фигуры составляются из треугольников, площади которых при движении со- храняются. Следовательно, и площади многоугольных фигур сохраняются. Для произвольных фигур утверждение следует из того, что произвольную фигуру можно приблизить многоугольной фигурой.

Определение 11.6. Две фигуры называются равными, если существует движение, переводящее одну из них в другую.

11.3 Виды движений

11.3.1 Параллельный перенос

Определение 11.7. Параллельным переносом фигуры называется такое ее преобразование, при ко- тором все точки фигуры перемещаются в одном и том же направлении на одно и то же расстояние, то есть на заданный вектор.

Теорема 11.3.1. Параллельный перенос является движением.

Доказательство.

Рассмотрим произвольный вектор a⃗ и соответствующий ему параллельный перенос T_a⃗. Необхо-

димо доказать, что для произвольных точек A и B расстояние AB равно расстоянию A^′B^′, где

A^′ = T (A),B^′ = T (B). Действительно, четырёхугольник AA^′B^′B – это параллелограмм, так как a⃗ a⃗

􏰁􏰁→ 􏰁􏰁→
AA^′ = BB^′ = a⃗, то есть AA^′ = BB^′ и AA^′ ∥ BB^′. Следовательно, AB = A^′B^′. Таким образом, параллель-

ный перенос сохраняет расстояние, то есть является движением.

Теорема 11.3.2. 1. Параллельный перенос сохраняет направления.
2. Движение, сохраняющее направления, является параллельным переносом.

Доказательство.

􏰁􏰁→ 􏰁􏰁→
Пусть X^′ = T (X),Y^′ = T (Y). Тогда XX^′ = YY^′ = a⃗. Следовательно, XX^′Y^′Y – это параллело-

^a⃗ _􏰁􏰁→ ^a⃗ 􏰁􏰁􏰁→ 􏰁􏰁􏰁→ _􏰁􏰁→
грамм, и, следовательно XY = X^′Y ^′, откуда следует, что X^′Y ^′ ⇈ XY , а это и означает, что движение

сохраняет направления.

􏰁􏰁→

Пусть движение f сохраняет направления, то есть для любого вектора XY будет выполняться 􏰁􏰁􏰁→ _􏰁􏰁→ 􏰁􏰁􏰁→ _􏰁􏰁→ X^′Y^′ ⇈XY,гдеX^′ =f(X),Y^′ =f(Y).Таккакf –этодвижение,тоX^′Y^′ =XY.АтаккакX^′Y^′ ⇈XY,

_􏰁􏰁→ 􏰁􏰁􏰁→ 􏰁􏰁→ то XY = X^′Y ^′. Из этого равенства следует, что XX^′Y ^′Y – параллелограмм, и, следовательно, XX^′ = 􏰁􏰁→
Y Y ^′. Последнее равенство означает, что движение f переносит любую точку на один и тот же вектор,

то есть по определению является параллельным переносом. 104

Теорема 11.3.3 (Параллельный перенос в координатах). Образ точки X(x₀;y₀) при параллельном переносе на вектор a⃗(x_a, y_a) имеет координаты X^′(x₀ + x_a; y₀ + y_a).

(x₀ +x_a;y₀ +y_a).
11.3.2 Осевая симметрия

Определение 11.8. Осевой симметрией относительно прямой l называется такое преобразование плоскости, при котором точки прямой l остаются неподвижными, а для любой точки A не лежащей на прямой l будет выполнено: AA^′ ⊥ l, ρ(A; l) = ρ(A^′; l), где A^′ – это образ точки A.

Теорема 11.3.4 (Осевая симметрия в координатах).

1. Образ точки X(x₀;y₀) при осевой симметрии относительно прямой l₁ ∶ y = a имеет координаты 
X^′(x₀; 2a − y₀);

2. Образ точки X(x₀;y₀) при осевой симметрии относительно прямой l₂ ∶ x = b имеет координаты 
X^′(2b − x₀; y₀);

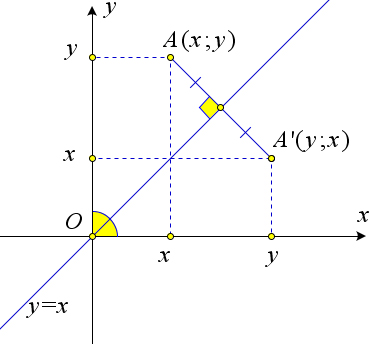
3. Образ точки X(x₀;y₀) при осевой симметрии относительно прямой l₃ ∶ x = y имеет координаты 
X^′(y₀; x₀).

Доказательство.

1. Пусть X^′ = S (X). Обозначим координаты точки X^′(x^′;y^′). Очевидно, что y^′ = y. Рассмотрим l1 
различные случаи расположения точки X относительно прямой l₁. Пусть x₀ > b. Тогда x^′ = b−AX = b−(x₀ −b) = 2b−x₀. Если x₀ = b, то x^′ = x₀ = 2b−x₀, то есть соотношение остаётся верным. Если же x₀ <b, то x^′ =b+AX =b+(b−x₀)=2b−x₀.

2. Пусть X^′ = S (X). Обозначим координаты точки X^′(x^′;y^′). Очевидно, что x^′ = x. Рассмотрим l2 
различные случаи расположения точки X относительно прямой l₂. Пусть y₀ > a. Тогда y^′ = a−AX = a−(y₀ −a) = 2a−y₀. Если y₀ = a, то y^′ = y₀ = 2a−y₀, то есть соотношение остаётся верным. Если же y₀ <a, то y^′ =a+AX =a+(a−y₀)=2a−y₀.

3. Прямая l₃ образует равные углы с осями координат (рис. 173 c). А так как движение сохраняет углы, а точка O остаётся неподвижной при осевой симметрии относительно прямой l₃, то образом оси абсцисс при осевой симметрии S_l3 является ось ординат, и наоборот. Следовательно, коорди- наты точки при осевой симметрии S_l3 меняются местами, то есть образом точки X(x;y) будет являться точка X^′(y;x).

Теорема 11.3.5. Осевая симметрия является движением. Доказательство.

Рассмотрим осевую симметрию S_l. Докажем, что S_l – это движение.

Доказательство.

^􏰁􏰁→ 􏰁􏰁→
Утверждение теоремы очевидно следует из цепочки равенств: X^′ = OX^′ = OX+a⃗ = (x₀;y₀)+(x_a,y_a) =

a) b) c) Рис. 173. Теорема 11.3.4.

105

Введем систему координат таким образом, чтобы прямая l совпадала с осью абсцисс. Возьмём любые две точки A(x₁,y₁) и B(x₂,y₂) и рассмотрим симметричные им относительно оси x точки A^′(x₁,−y₁) и B^′(x₂,−y₂). По формуле расстояния между двумя точками

A^′B^′ =^√(x₂ −x₁)² +(−y₂ +y₁)² =^√(x₂ −x₁)² +(y₂ −y₁)² =AB.

Таким образом, осевая симметрия сохраняет расстояния, то есть является движением.

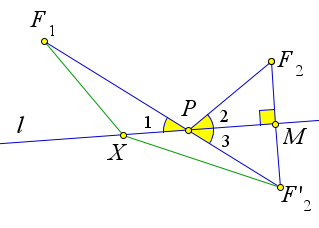
Теорема 11.3.6. Пусть точки F₁ и F₂ лежат по одну сторону от прямой l. Сумма расстояний F₁ P + P F₂ , где точка P лежит на прямой будет наименьшей, если лучи P F₁ и P F₂ образуют равные углы с прямой l.

Рис. 174. Теорема 11.3.6.

Доказательство.

Пусть F₂^′ = S_l(F₂). Пусть прямая F₁F₂^′ пересекает прямую l в точке P. Тогда, так как PF₂ = PF₂^′, то F₁P +PF₂ =F₁P +PF₂^′. Для любой точки X прямой l, отличной от точки P, с учётом неравенства треугольника будет верно F₁X +XF₂^′ = F₁X +XF₂^′ > F₁F₂^′ = F₁F₂. Таким образом сумма F₁P +P F₂ будет наименьшей. Докажем теперь, что _∠1 = _∠2. Действительно, треугольник F₂PF₂^′ равнобедренный, и, следовательно, высота PM является биссектрисой. Тогда _∠2 = _∠3. Но _∠1 = _∠3, как вертикальные. Следовательно, _∠1 = _∠2.

11.3.3 Центральная симметрия

Определение 11.9. Центральная симметрия относительно точки O – это такое преобразование плос- 􏰁􏰁→ ^􏰁􏰁→

кости, которое любой точке X сопоставляет такую точку X^′, что OX = −OX^′.
Теорема 11.3.7. Центральную симметрию можно представить в виде композиции двух осевых

симметрий относительно взаимно перпендикулярных прямых, проходящих через центр симметрии.

Доказательство.

Рассмотрим центральную симметрию, относительно точки O. Рассмотрим произвольные взаимно

перпендикулярные прямые l₁ и l₂, проходящие через точки O. Докажем, что Z_O = S_l2 ○ S_l1 . Для этого

докажем,чтодляпроизвольнойточкиX будетвыполненоX^′ =X^′′,гдеX^′ =Z_O(X),X^′′ =S_l2(S_l1(X)).

Пусть Y = S (X) и S (Y) = X^′′. Тогда _△X^′YX – прямоугольный, кроме того OX = OY = OX^′′. ^l1 ^l2

􏰁􏰁→ ^􏰁􏰁→
Следовательно, OX = −OX^′′, то есть X^′′ = X^′.

Теорема 11.3.8. Центральная симметрия является движением.

Доказательство.

Так как центральная симметрия представляется в виде композиции двух осевых симметрий, а ком- позиция движений является движением, то центральная симметрия также является движением.

Теорема 11.3.9 (Центральная симметрия в координатах). Образ точки X(x₁;y₁) при центральной симметрии относительно точки O(x₀; y₀) имеет координаты X^′(2x₀ − x₁; 2y₀ − y₁).

((x₁; y₁) − (x₀; y₀)) = (2x₀ − x₁; 2y₀ − y₁).

Доказательство.

􏰁􏰁→ Утверждение теоремы очевидно следует из следующей цепочки равенств: X^′ = O − OX = (x₀; y₀) −

106

11.3.4 Поворот

Определение 11.10. Поворотом фигуры вокруг точки O на угол φ называется такое преобразование, которое каждую точку X переводит в точку X^′, при этом OX = OX^′ и угол XOX^′ отложенный в заданном направлении от луча OX равен φ.

Теорема 11.3.10. Поворот можно представить в виде композиции двух осевых симметрий.

Доказательство.

Рассмотрим поворот R_O,φ. Докажем, что R_O,φ = S_l2 ○S_l1 , где прямые l₁ и l₂ пересекаются в точке O под углом ^φ . Необходимо доказать, что для любой точки X будет выполнено X^′ = X^′′, где X^′ = R_O,φ(X)

2

и X^′′ = S_l2 (S_l1 (X)).

Если X = O, то равенство X = X^′′ очевидно, так как точка O остаётся неподвижной.

Пусть Y = S_l1 (X). Тогда _∠(X; l₁) = _∠(Y ; l₂), обозначим эти углы α. Кроме того, пусть β = _∠(X; l₂).

Если α < β и α < ^φ 2

Теорема 11.3.11. Поворот является движением.
Теорема 11.3.12 (Поворот в координатах). При повороте на угол φ вокруг начала координат в по-

ложительном направлении образ X(x;y) и X^′(x^′;y^′) связаны соотношениями: _{ x^′ =xcosφ−ysinφ, _{ x=x^′cosφ+y^′sinφ,

y^′ =xsinφ+ycosφ; y=y^′cosφ−x^′sinφ. 11.4 Классификация движений

Теорема 11.4.1 (о единственности движения). Пусть у двух движений f и g фигуры M образы неко- торых точек A,B и C, не лежащих на одной прямой, совпадают, то есть f(A) = g(A) = A^′,f(B) = g(B) = B^′,f(C) = g(C) = C^′. Тогда движения f и g совпадают, то есть f(X) = g(X) для любой точки X фигуры M.

Теорема 11.4.2 (о задании движения). Пусть на плоскости заданы два равных треугольника ABC и A^′B^′C^′, причем A^′B^′ = AB, A^′C^′ = AC, B^′C^′ = BC. Тогда существует такое движение плоскости, которое переводит точку A в A^′, B в B^′, C в C^′.

Теорема 11.4.3. Композиция движений является движением.

Теорема 11.4.4 (теорема Шаля). Каждое движение на плоскости является либо переносом, либо поворотом, либо композицией осевой симметрии и переноса в направлении оси симметрии (то есть скользящего отражения).

Теорема 11.4.5.

1. Если у движения нет неподвижных точек, то это перенос на ненулевой вектор или скользящая симметрия.

2. Если у движения одна неподвижная точка, то это поворот.

3. Если множеством неподвижных точек движения является прямая, то это осевая симметрия.

4. Если множеством неподвижных точек движения является вся плоскость, то это тожде- ственное преобразование.

Определение 11.11.

1. Движения, которые могут быть реализованы непрерывными перемещениями, называются дви- жениями первого рода. (Перенос, поворот).

2. Движения, которые не могут быть реализованы непрерывными перемещениями, называются дви- жениями второго рода. (Осевая симметрия).

107

11.5 Гомотетия

Определение 11.12. Преобразование фигуры называется подобием с коэффициентом k > 0, если любым двум точкам X и Y этой фигуры сопоставляются точки X^′ и Y ^′ такие, что ∣X^′Y ^′∣ = k∣XY ∣.

Определение 11.13. Фигура F ^′ называется подобной фигуре F с коэффициентом k, если существует подобие с коэффициентом k, переводящее фигуру F в фигуру F^′.

Определение 11.14. Гомотетия с центром в точке O и коэффициентом k ≠ 0 – это такое преобразо- ^􏰁􏰁→ 􏰁􏰁→

вание плоскости, которое каждой точке X сопоставляет такую точку X^′, что OX^′ = kOX.
Теорема 11.5.1 (Гомотетия в координатах). Образ точки X(x; y) при гомотетии с центром O(x₀; y₀)

и коэффициентом k будет иметь координаты X^′(x₀ + k(x − x₀); y₀ + k(y − y₀)).
Теорема 11.5.2. При гомотетии с коэффициентом k каждый вектор умножается на k.

Теорема 11.5.3. Подобие с коэффициентом k – это композиция движения и гомотетии с коэффи- циентом k.

Теорема 11.5.4 (Свойства гомотетии).

1. Гомотетия отрезок переводит в отрезок.

2. Гомотетия сохраняет величину угла.

3. Гомотетия треугольник переводит в треугольник. Стороны этих треугольников пропорцио- нальны, а соответственные углы равны.

4. Композиция двух гомотетий с общим центром и с коэффициентами k₁ и k₂ будет гомотетий 
с тем же центром и коэффициентом k₁ ⋅ k₂. Преобразование, обратное гомотетии с данным 
центром и коэффициентом k, будет гомотетией с тем же центром и коэффициентом ¹ . k

Теорема 11.5.5 (Свойства подобия).

1. Подобие отрезок переводит в отрезок.

2. Подобие сохраняет величину угла.

3. Подобие треугольник переводит в треугольник. Стороны этих треугольников пропорциональ- ны, а соответственные углы равны.

4. В результате подобия с коэффициентом k площадь фигуры умножается на k².

5. Композиция двух подобий с коэффициентами k₁ и k₂ будет подобием с коэффициентом k₁ ⋅ k₂.

6. Подобие обратимо, и преобразование обратное подобию с коэффициентом k? есть подобие с 
коэффициентом ¹. k

108