7 Правильные многоугольники

Определение 7.1. Многоугольник называется правильным, если все его стороны равны и все его углы равны.

Теорема 7.0.13 (о центре правильного многоугольника). В каждом правильном многоугольнике есть точка, равноудаленная от всех его сторон и от всех его вершин.

Доказательство.

Рассмотрим правильный многоугольник. Обозначим α = _∠A. Проведем в нём биссектрисы углов A и B. Пусть они пересекаются в точке O. Докажем, что Биссектрисы остальных углов данного много- угольника тоже проходят через точку O.

Так как OA и OB – это биссектрисы, а углы правильного многоугольника равны, то _∠1 = _∠2 = _∠3 = _∠4 = ¹α. Следовательно, треугольник AOB равнобедренный, то есть OA = OB. Кроме того

2

_△AOB = _△BOC по первому признаку равенства (OA = OB,AB = BC,_∠2 = _∠4). Следовательно, OB = OC и _∠5 = _∠3 = ¹ α. Таким образом OC является биссектрисой угла C, а точка O равноудалена

2

от вершин A,B и C. Аналогичные рассуждение теперь можно провести для вершины D, и потом по очереди для всех других вершин многоугольника.

Таким образом точка O равноудалена от всех вершин многоугольника, в силу равенства треуголь- ников, кроме того точка O равноудалена от всех сторон многоугольника, так как это точка пересечение биссектрис.

Следствие 7.0.13.1. Для любого правильного многоугольника существует вписанная и описанная окружность, причём их центры совпадает. Вписанная и описанная окружность для правильного многоугольника единственны.

Доказательство.

Существование и совпадение центров вписанной и описанной окружности непосредственно следуют из теоремы 7.0.13.

Докажем единственность. Рассмотрим какие-нибудь три вершины многоугольника, например A,B,C. Так как через эти точки проходит только одна окружность, то около многоугольника можно описать только одну окружность.

Теперь предположим, что в правильный многоугольник можно вписать окружность с центром O и радиусом OM и другую окружность с центром O₁ и радиусом O₁M₁. Тогда центр O₁ равноудалён от всех сторон многоугольника, следовательно, точка O₁ лежит на каждой из биссектрис углов много- угольника и, следовательно, совпадает с точкой O пересечения этих биссектрис. Радиус окружности O₁M₁ равен расстоянию от точки O до сторон многоугольника, то есть OM. Таким образом вторая окружность совпадает с первой.

Следствие 7.0.13.2. Окружность, вписанная в правильный многоугольник, касается сторон мно- гоугольника в их серединах.

Доказательство.

Утверждение следует из того, что радиус вписанной окружности является высотой равнобедренного треугольника AOB.

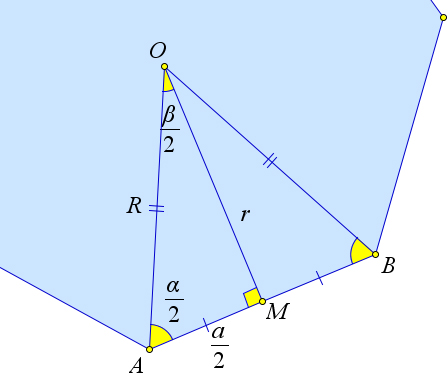
Теорема 7.0.14. Пусть α – это угол правильного n-угольника, а β – угол между радиусами описан- ной окружности, проведёнными к соседним вершинам. Тогда выполняются следующие соотношения

_{1. α=}^180X(n−2)_{, β=}360^X_. nn

2. a=2Rsin^β =2Rcos^α. 22

3. a=2rtg^β =2rctg^α. 22

4. r=Rcos^β =Rsin^α. 22

5. S=pr=¹nr²sinβ. 2

75

Доказательство.

Рис. 124. Теорема 7.0.14.

1. По теореме 2.1.3 сумма углов n-угольника равна 180^○(n − 2), следовательно, каждый угол будет равен α = ¹⁸⁰X ⁽ⁿ⁻²⁾ . Кроме того полный угол O разделён радиусами, проведёнными к вершинам

ⁿ_X многоугольника, на n частей, следовательно, β = ³⁶⁰ .

n

Проведем высоту OM треугольника AOB. Так как треугольник AOB равнобедренный, то _∠AOM = ^β, AM = ^a. Кроме того _∠OAM = ^α. Из треугольника AOM получаем a = 2rtg^β =

2rctg ^α. 2

2222

2. sin^β =cos^α = a , следовательно, a=2Rsin^β =2Rcos^α. 22R22

3. tg ^β = ctg ^α = a , следовательно, 22r

4. cos^β =sin^α = ^r,следовательно,r=Rcos^β =Rsin^α. 22R22

5. ФормулаS=prследуетизтеоремы6.6.4.CдругойстороныS=n⋅S_AOB =n⋅¹R²sinβможно 2

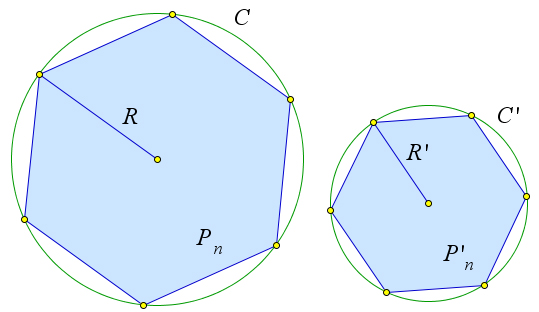
Следствие 7.0.14.1. Периметры правильных n-угольников относятся как радиусы описанных около них окружностей.

Доказательство.

Рассмотрим два правильных n-угольника со сторонами a_n и a^′_n соответственно. Используя формулы

2

2

из пунктов 1 и 2 теоремы 7.0.14 выпишем периметры P_n и P_n^′ данных многоугольников: P_n = n ⋅ a_n =

n⋅2Rsin¹⁸⁰X,P^′ =n⋅a^′ =n⋅2R^′sin¹⁸⁰X.Следовательно, ^Pn = ^2R = ^R. nⁿⁿ n P_n^œ2R^œR^œ

Теорема 7.0.15 (правильный треугольник).

1. α=60^○. √

2. S = ^a2 ³ . 4

√

3.h=^{a 3}. 2

√

4.r=^{a 3}. 6

√

5.R=^{a 3}. 3

6. R=2r.

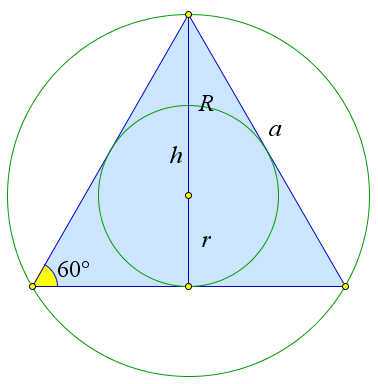
Рис. 125. Теорема 7.0.15.

76

Доказательство.

1.α=¹⁸⁰X =60^○. 3

√√ 2.S=¹a²sin60^○=¹a^{2 3}=^a2 ³.

2224

_a^2­₃ √ 3.h=^2S= ² =^{a 3}.

aa2 _a^2­₃ √

4.r=^S= ⁴ =^{a 3}. p ^3a 6

2

√

4S _a² ₃ 3
6. R = 2r, в силу предыдущих двух пунктов.

Теорема 7.0.16 (Квадрат). 1. α=90^○.

2. S=a².

3. d=a^√2.

4. r = ^a . 2

√

5.R=^{a 2}. 2

Рис. 126. Теорема 7.0.16.
Доказательство. _{√ √}

33

aaa3 5.R= = ^√ = .

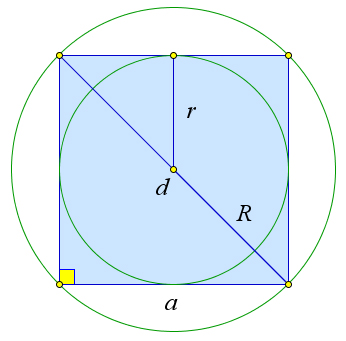
Первые два пункта теоремы очевидны. Третий следует из теоремы Пифагора d = a² + a² = a 2. √

r=^S=^a2 =^a,R=^d=^{a 2}. p 2a 2 2 2

Теорема 7.0.17 (Правильный шестиугольник).

1. α=120^○.

2.R=a,r=^{a 3}

2
3. d₁ =2a, d₂ =a^√3

√

4. Малая диагональ правильного шестиугольника перпендикулярна его стороне.

5. Противоположные стороны правильного шестиугольника параллельны между собой, а также параллельны большой диагонали. 
√

6. _{S =} ^{3a2 3} _. 2

77

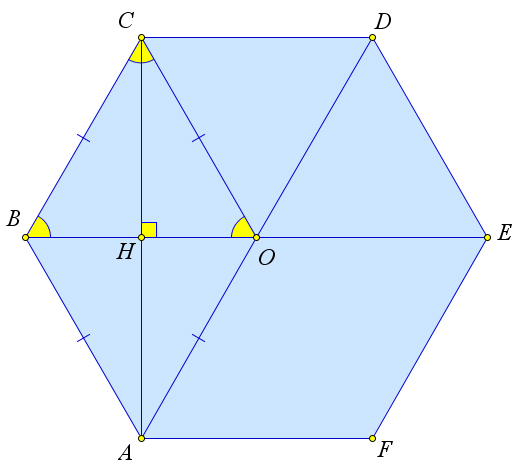
Доказательство.

1. 2.

3. 4. 5.

_{α =} ^180X(6−2) _{= 120○.} 6

Рис. 127. Теорема 7.0.17.

Так как BO и CO – биссектрисы, то _∠CBO = _∠BCO = 60^○. Следовательно, треугольник BOC

√

равносторонний. Значит R = a, r = ^a значит BE – диагональ, и BE = 2R = 2a.

³ _.
∠BOC + _∠COD + _∠DOE = 3 ⋅ 60^○ = 180^○. Следовательно, точки B, O и E лежат на одной прямой,

2

Четырёхугольник OABC – ромб, следовательно, OB ⊥ AC. Четырёхугольник OBCD – ромб, поэтому BO ∥ CD. Следовательно AC ⊥ CD.

√ S = 6 ⋅ S_AOB = 6 ¹ a² sin 60^○ = ^3a2 ³ .

Длина окружности. Площадь круга

8

22

Определение 8.1. Длина окружности – это предел, к которому стремится периметр правильного вписанного в окружность многоугольника при неограниченном увеличении числа его сторон.

Определение 8.2. Длина кривой линии приближённо равна длине вписанной ломанной и вычисля- ется она тем точнее, чем меньше звенья ломанной и чем чаще располагаются вершины ломанной на данной кривой.

Теорема 8.0.18. Длина окружности пропорциональна ее радиусу, то есть отношение длины окруж- ности к ее радиусу не зависит от окружности.

Рис. 128. Теорема 8.0.18.

Доказательство.

Пусть C и C^′ – длины окружностей радиусов R и R^′ (рис. 128). Впишем в каждую из них правиль- ный n-угольник и обозначим через P_n и P_n^′ их периметры.

По следствию 7.0.14.1 имеем
Это равенство справедливо при любом значении n. Будем теперь неограничено увеличивать число n.

^Pn = ^2R . (1) P_n^′ 2R^′

ТаккакP →C,P^′ →C^′ приn→∞,то ^Pn = ^C.Тогдавсилуравенства(1) ^C = ^2R.Изэтого ^{n n} œ P_n^œ C^œ C^œ 2R^œ

равенства следует, что ^C = ^C _œ . 2R 2R

Определение 8.3. Отношение длины окружности к её диаметру обозначается числом π. То есть

^C = π. Таким образом длина окружности вычисляется по формуле C = 2πR. 2R

78

Теорема 8.0.19. Периметры P правильных n-угольников, описанных около окружности F, прибли- жаются к длине окружности F.

Рис. 129. Теорема 8.0.19.

Доказательство.

Пусть правильный n-угольник Q описан около окружности F с радиусом R и центром O (рис. 129). Соединим отрезками точку O с вершинами многоугольника Q. Эти отрезки пересекут окружность F в точках, которые являются вершинами правильного n-угольника Q^′, вписанного в F. пусть сторона AB n-угольника Q касается окружности F в точке C, а отрезки OA и OB пересекают F в точках A^′ и B^′. Радиус OC пересечёт отрезок A^′B^′ в середине – точке C^′.

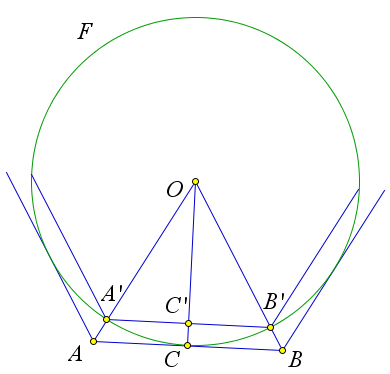
Отношение периметров P и P ^′ правильных n-угольников Q и Q^′ равно отношению их сторон AB и

A^′B^′,тоестьотношениюихполовин ^AC .ИтаккакAC=Rtg¹⁸⁰X иA^′C^′ =Rsin¹⁸⁰X,то ^P = ¹ X .

A^œC^œ n n P^œ _cos ¹⁸⁰ n

ПоэтомуP= ^Pœ X. cos ¹⁸⁰

n

ности F.

Теорема 8.0.20. Длина дуги окружности, соответствующей центральному углу в α^○, равна l_α = 2πRα_.

360

Доказательство.

ⁿ_X Когда число n неограниченно увеличивается, cos ¹⁸⁰

приближается к cos0^○, то есть к 1, а P^′ – к длине окружности F, то есть к 2πR. Следовательно, периметры P правильных n-угольников, описан- ных около окружности F, как и периметры вписанных n-угольников, приближаются к длине окруж-

Так как длина всей окружности равна 2πR, то длина дуги в 1^○ равна ^2πR. Поэтому длина дуги, 360

соответствующей центральному углу в α^○ выражается формулой l_α = ^2πR ⋅ α. 360

Теорема 8.0.21 (о площади круга). Площадь S круга радиуса R выражается формулой S = πR².

Рис. 130. Теорема 8.0.21.

Доказательство.

Рассмотрим правильный n-угольник A₁A₂ ...A_n, вписанный в окружность, ограничивающую круг (рис. 130). Очевидно, площадь S данного круга больше площади S_n многоугольника A₁A₂ ...A_n, так как этот многоугольник целиком содержится в данном круге. С другой стороны, площадь S_n^′ круга, вписанного в многоугольник, меньше S_n, так как этот круг целиком содержится в многоугольнике. Итак, S^′n < S_n < S. _X

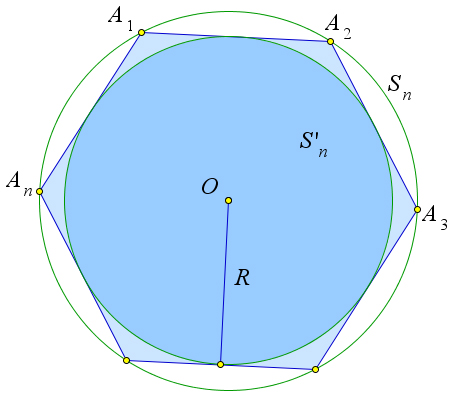
По пункту 4 теоремы 7.0.14 имеем r_n = R cos ¹⁸⁰ , где r_n – радиус вписанной в многоугольник _Xⁿ

окружности. При n → ∞ cos ¹⁸⁰ → 1, поэтому r_n → R. Иными словами, при неограниченном увеличении n

79

числа сторон многоугольника вписанная в него окружность «стремиться» к описанной окружности, поэтому S_n^′ →S при n→∞.

По теореме 6.6.4 S_n = ¹P_nr_n, где P_n – периметр многоугольника A₁A₂ ...A_n. Учитывая, что r_n → 2

R, P_n → 2πR, S_n → S при n → ∞, получаем S = ¹ 2πR ⋅ R = πR². 2

Следствие 8.0.21.1.

1. Площадь сектора, соответствующего центральному углу в α^○, выражается формулой S_сек = πR²α_. 
360

2. Площадь сегмента, соответствующего центральному углу в α^○, выражается формулой S_сегм = ^πR2^α − ¹R² sinα.

Доказательство.

360 2

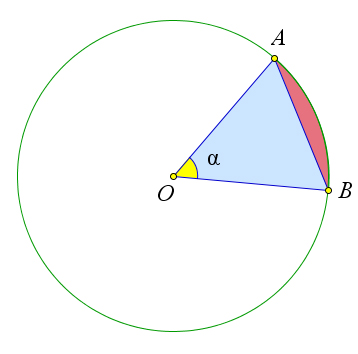
Рис. 131. Следствие 8.0.21.1.

Докажем первый пункт. Так как площадь всего круга равна πR², то площадь сектора, ограничен- ного дугой в 1^○, равна ^πR2 . Поэтому площадь S сектора, ограниченного дугой в α^○ равна S = ^πR2 ⋅ α.

360 360

Докажем второй пункт. Площадь сегмента равна разности площади сектора и площади треуголь- никаAOB,такимобразомS =S −S =^πR2^α −¹R²sinα.

^{сегм сек} _△AOB _{360 2} 9.1 Определение вектора

9 Векторы

Определение 9.1. Величина, которая характеризуется своим численным значением, направлением и складывается по правилу треугольника, называется векторной величиной.

Определение 9.2. Направленный отрезок – это отрезок один конец которого считается началом, а другой концом.

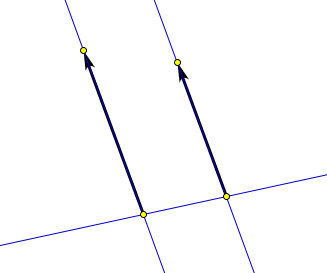
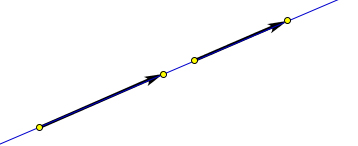
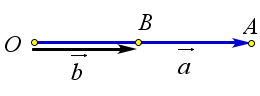
Определение 9.3. Направленные отрезки называются сонаправленными, если выполняется одно из двух следующих условий:

1. отрезки лежат на одной прямой, и лучи, задаваемые этими отрезками в пересечении дают луч (рис. 132 a);

2. отрезки лежат на параллельных прямых, и их концы лежат в одной полуплоскости относительно прямой, соединяющей начала направленных отрезков (рис. 132 b).

a)

Рис. 132. Определение 9.3.

80

b)

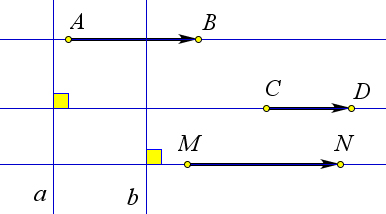
Определение 9.4. Направленные отрезки называются сонаправленными, если они лежат на парал- лельных прямых или на одной прямой, и при этом лучи, задаваемые этими направленными отрезками лежат по одну сторону от некоторой непараллельной им прямой, то есть в одной полуплоскости, огра- ниченной этой прямой (рис. 133).

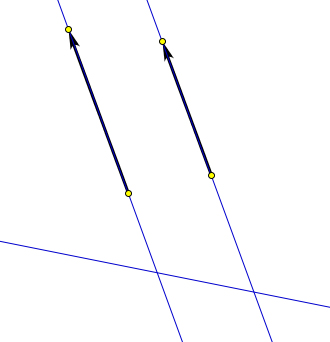
Рис. 133. Определение 9.4. 􏰁→ 􏰁􏰁→

Определение 9.5. Векторы AB и CD сонаправлены, если найдётся такая прямая a, что, во-первых, они перпендикулярны этой прямой и, во-вторых, лучи AB и CD лежат по одну сторону от этой прямой (рис. 134).

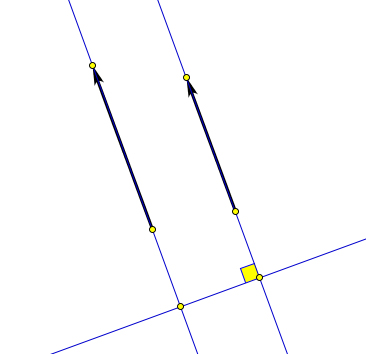
Рис. 134. Определение 9.5. Утверждение 9.1.1. Определения 9.3, 9.4 и 9.5 эквивалентны.

Определение 9.6. Направленные отрезки называются противоположно направленными, если выпол- няется одно из двух следующих условий:

1. отрезкилежатнаоднойпрямой,илучи,задаваемыеэтимиотрезкамивпересечениидаютотрезок, точку или пустое множество;

2. отрезки лежат на параллельных прямых, и их концы лежат в разных полуплоскостях относи- тельно прямой, соединяющей начала направленных отрезков.

b)

a)

Рис. 135. Определение 9.6.
Определение 9.7. Направленные отрезки называются противоположно направленными, если они

лежат на параллельных прямых (или на одной прямой), но не сонаправлены. Замечание. Определения 9.6 и 9.7 эквивалентны.

81

Определение 9.8. Направленные отрезки называются равными, если они равны по длине и сона- правлены.

Определение 9.9. Вектор – это класс эквивалентности направленных отрезков, по отношению экви- валентности «равенство» (или проще: класс равных направленных отрезков).

􏰁→ _⃗

Определение 9.10. Для любой точки A, вектор AA называется ноль-вектором и обозначается 0. Определение 9.11. Вектора называются коллинеарными, если их направленные отрезки сонаправ-

лены или противоположно направлены.

Теорема 9.1.2. Два вектора сонаправленные с третьим вектором, сонаправлены.

Рис. 136. Теорема 9.1.2.
Доказательство. _{􏰁→ 􏰁􏰁→ 􏰁􏰁→ 􏰁→ 􏰁􏰁→}

Пусть векторы AB и CD сонаправлены с вектором MN (рис. 136). Докажем, что AB ⇈ CD. Так

􏰁→ 􏰁􏰁→
как AB ⇈ M N , то по определению 9.5 найдется такая перпендикулярная им прямая a, от которой лучи

AB и MN лежат по одну сторону. Точно так же для векторов CD и MN найдётся перпендикулярная им прямая b, от которой лучи CD и MN лежат по одну сторону. Если прямые a и b не совпадают, то они параллельны (как перпендикулярные одной и той же прямой MN). Тогда из двух полуплоскостей, которые ограничены прямыми a и b и содержат луч MN, одна содержит другую. Будем считать, что это полуплоскость ограниченная прямой a. Эта полуплоскость содержит лучи AB, CD и MN. Тем

самым выполнено второе условие определения 9.5. Кроме того выполнено и первое условие, так как

􏰁→ 􏰁􏰁→ 􏰁→ 􏰁􏰁→ векторы AB и CD перпендикулярны прямой a. Поэтому AB ⇈ CD.

􏰁􏰁→ 􏰁􏰁→

Определение 9.12. Векторы называются равными, если их длины равны и они сонаправлены. Теорема 9.1.3. 1. Каждый вектор равен самому себе.

2. Если вектор a⃗ равен вектору ^⃗b, то вектор ^⃗b равен вектору a⃗.

3. Два вектора равные третьему вектору, равны.

Доказательство.

Первые два свойства очевидно вытекают из определения равенства векторов.

Докажем третье свойство. Пусть a⃗ = ^⃗b и c⃗ = ^⃗b. Тогда ∣a⃗∣ = ∣^⃗b∣ и a⃗ ⇈ ^⃗b, а также ∣c⃗∣ = ∣^⃗b∣ и c⃗ ⇈ ^⃗b. Из равенства модулей следует, что ∣a⃗∣ = ∣c⃗∣. А из теоремы 9.1.2 вытекает, что a⃗ ⇈ c⃗. Поэтому a⃗ = c⃗.

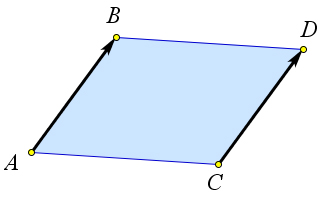
􏰁→ 􏰁􏰁→ Теорема 9.1.4. Если четырехугольник ABCD – параллелограмм, то AB = DC.

Рис. 137. Теорема 9.1.4.

Доказательство.

Из того, что ABCD параллелограмм следует, что AB = CD и AB ∥ CD (рис. 137). Кроме того лучи

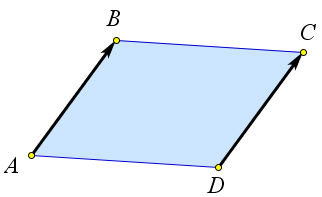
AB и DC лежат по одну сторону от прямой AD, следовательно вектора AB и DC сонаправлены и 􏰁→ 􏰁􏰁→

равны по модулю. Таким образом AB = DC.

􏰁→ 􏰁􏰁→

82

􏰁→ 􏰁􏰁→ 􏰁→ 􏰁􏰁→ Теорема 9.1.5. Если AB = CD, то AC = BD.

Рис. 138. Теорема 9.1.5.

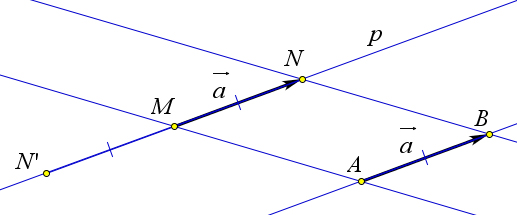
Теорема 9.1.6. От любой точки M можно отложить вектор, равный данному вектору a⃗, и при том только один.

Рис. 139. Теорема 9.1.6.

􏰁→
Рассмотрим вектор AB = a⃗ (рис. 139). Проведем через точку M прямую p, параллельную AB

(если M – точка прямой AB, то в качестве прямой p возьмём саму прямую AB). На прямой p отложим отрезки MN и MN^′, равные отрезку AB, и выберем из векторов MN и MN^′ тот, который сонаправлен с вектором a. Этот вектор и является искомым вектором, равным вектору a. Единственность следует из аксиомы 1 (об откладывании отрезка) и аксиомы 4 (о параллельных прямых).

9.2 Линейные операции с векторами

Доказательство.

􏰁→ 􏰁􏰁→
Из равенства векторов AB и CD следует, что AB = CD и AB ∥ CD, таким образом ABDC –

􏰁→ 􏰁􏰁→ параллелограмм (рис. 138). Следовательно, по теореме 9.1.4 AC = BD.

Доказательство.

Определение 9.13 (Правило треугольника). Чтобы получить сумму векторов a⃗ и ^⃗b, нужно от какой- 􏰁→ 􏰁→ _⃗

либо точки A отложить вектор AB = a⃗, затем от точки B отложить вектор BC = b (рис. 140). Вектор 􏰁→ _{⃗ ⃗} 􏰁→ 􏰁→ 􏰁→
AC называется суммой векторов a⃗ и b. a⃗+b=AB+BC =AC

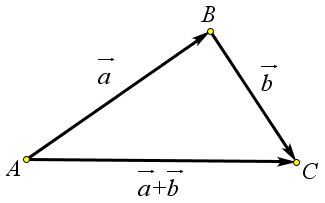
Рис. 140. Теорема 9.13.

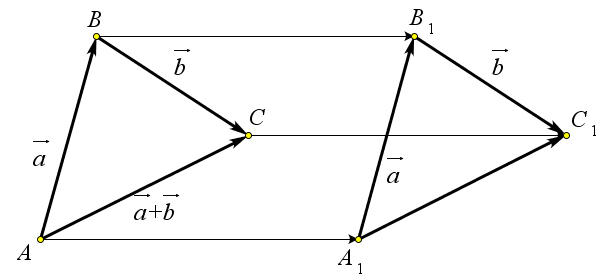
Теорема 9.2.1. Определение 9.13 корректно, то есть сумма векторов не зависит от выбора точки A.

Рис. 141. Теорема 9.2.1.

83

Доказательство.

􏰁􏰁􏰁→
Докажем, что если отложить вектор a от точки A₁, то есть A₁B₁ = a⃗, а затем от точки B₁ отложить

􏰁􏰁􏰁→ _⃗ 􏰁􏰁􏰁→ 􏰁􏰁􏰁→ 􏰁􏰁􏰁→ 􏰁→
вектор B₁C₁ = b, то сумма векторов A₁B₁ + B₁C₁ = A₁C₁ будет равна вектору AC, то есть A₁C₁ = AC

^{(рис. 141).} 􏰁→ 􏰁􏰁􏰁→ 􏰁􏰁→ 􏰁􏰁→ 􏰁􏰁􏰁→ 􏰁→ Так как AB = A₁B₁, то по теореме 9.1.5 имеем AA₁ = BB₁. Аналогично из равенства B₁C₁ = BC

􏰁􏰁→ 􏰁􏰁→ 􏰁􏰁→ 􏰁􏰁→
следует, что BB₁ = CC₁. Поэтому AA₁ = CC₁. Но из этого равенства по той же теореме 9.1.5 следует,

􏰁􏰁􏰁→ 􏰁→ что A₁C₁ = AC.

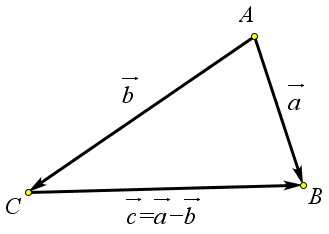
Определение 9.14. Разностью векторов a⃗ и ^⃗b называется такой вектор c⃗, что c⃗ + ^⃗b = a⃗. Принято обозначать c⃗ = a⃗ − ^⃗b (рис. 142).

Рис. 142. Определение 9.14. Следствие 9.2.1.1. AB − AC = CB (рис. 142).

􏰁􏰁􏰁→ 􏰁→

􏰁→ 􏰁→ 􏰁→
Теорема 9.2.2 (Правило параллелограмма). Если ABCD – параллелограмм, то AB + AD = AC

􏰁→ 􏰁→ 􏰁→

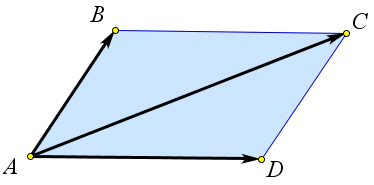
Рис. 143. Теорема 9.2.2.

􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→ Так как ABCD – параллелограмм, то AD = BC. Следовательно, AB + AC = AB + BC = AC.

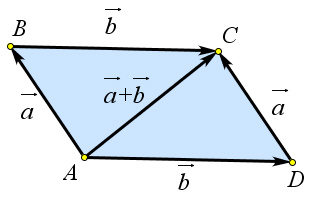
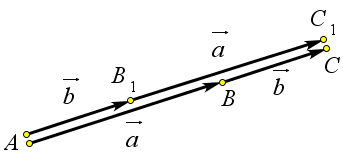
Теорема 9.2.3 (свойства сложения векторов). Для любых векторов a⃗,^⃗b и c⃗ 1. a⃗+0^⃗=a⃗.
2. a⃗+^⃗b=^⃗b+a⃗.
3. (a⃗+^⃗b)+c⃗=a⃗+(^⃗b+c⃗).

Доказательство.

a)

c)

b)

d)

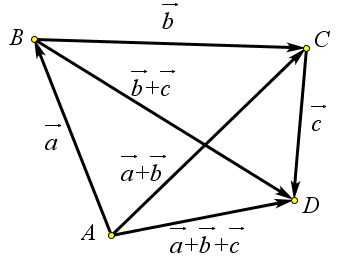
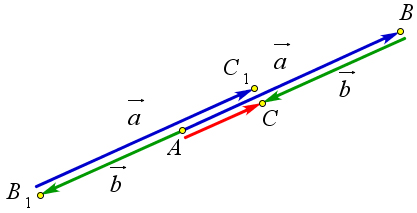
Рис. 144. Теорема 9.2.3.

84

Доказательство. _⃗

Первой свойство очевидно. Докажем второе свойство. Возможны два случая: 1) векторы a⃗ и b

неколлинеарны, 2) вектора a⃗ и ^⃗b коллинеарны. Рассмотрим первый случай. Пусть вектора a⃗ и ^⃗b некол- 􏰁→ 􏰁→

линеарны. Отложим их от точки A: AB = a и AD = b – и построим на этих векторах параллелограмм 􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→ 􏰁→ _{⃗ ⃗ ⃗}

ABCD (рис. 144 a). Поскольку AB+BC = AC,AD+DC = AC,AB+DC = a⃗ и BC = AD = b, то a⃗+b = b+a⃗.

Рассмотрим второй случай. Пусть вектора a⃗ и ^⃗b коллинеарны. Если вектора a⃗ и ^⃗b сонаправлены, _⃗ 􏰁→ 􏰁→ 􏰁→

то можно их последовательно отложить от точки A двумя способами, то есть a⃗ + b = AB + BC = AC, _⃗ 􏰁􏰁→ 􏰁􏰁􏰁→ 􏰁􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→ 􏰁􏰁→

или b + a⃗ = AB₁ + B₁C₁ = AC₁ (рис. 144 b). Докажем, что AC = AC₁. Вектора AC и AC₁ очевидно сонаправлены, кроме того их модули равны ∣a⃗∣ + ∣^⃗b∣. Следовательно, эти вектора равны.

Рассмотрим случай, когда вектора a⃗ и ^⃗b противоположно направлены (рис. 144 c). Пусть кроме того _{⃗ ⃗} 􏰁→ 􏰁→ 􏰁→ 􏰁→ _{⃗ ⃗} 􏰁􏰁→ 􏰁􏰁􏰁→ 􏰁􏰁→

∣a⃗∣ > ∣b∣. Тогда a⃗+b = AB+BC = AC, при этом ∣AC∣ = ∣a⃗∣−∣b∣. C другой стороны b+a⃗ = AB₁+B₁C₁ = AC₁, при 􏰁􏰁→ _⃗ 􏰁→􏰁􏰁→

этом ∣AC₁∣ = ∣a⃗∣ − ∣b∣. Таким образом модули векторов AC и AC₁ равны, кроме того они сонаправлены,

􏰁→ 􏰁􏰁→ следовательно, AC = AC₁.

􏰁→
Докажем третий пункт теоремы. Отложим от точки A вектор AB = a⃗, затем от точки B вектор

􏰁→ _⃗ 􏰁􏰁→
BC = b, а потом от точки C вектор CD = c⃗(рис. 144 d). Тогда (a⃗+b)+c⃗= (AB+BC)+CD = AC+CD = AD.

_⃗ 􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→ _⃗ 􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→ _{⃗ ⃗}

C другой стороны, a⃗+(b+c⃗)=AB+(BC+CD)=AB+BD=AD. Итак (a⃗+b)+c⃗=a⃗+(b+c⃗).

Определение 9.15. Два ненулевых вектора называются противоположными, если их длины равны и они противоположны по направлению. Ноль-вектор считается противоположным самому себе (рис. 145).

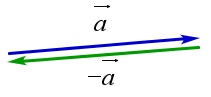
Теорема 9.2.4.

1. a⃗+(−a⃗)=0^⃗.

2. Если a⃗+^⃗b=^⃗0, то a⃗=−^⃗b. Доказательство.

Рис. 145. Определение 9.15.

􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→ _⃗ Докажем первый пункт. Пусть a⃗ = AB. Тогда −a⃗ = BA. Следовательно, a⃗ + (−a⃗) = AB + BA = AA = 0.

_{⃗ ⃗} 􏰁→ _⃗ 􏰁→ _⃗ 􏰁→ Докажем второй пункт. Пусть a⃗ + b = 0. Тогда, если a⃗ = AB, то поскольку 0 = AA, то b = BA. Таким

Теорема 9.2.5. Для любых двух векторов a⃗ и ^⃗b справедливо равенство a⃗ − ^⃗b = a⃗ + (−^⃗b).

Рис. 146. Теорема 9.2.5.

называется такой вектор xa⃗, для которого выполняются два условия: 85

образом, вектора a⃗ и ^⃗b равны по модулю и противоположны по направлению, то есть векторы a⃗ и ^⃗b противоположны.

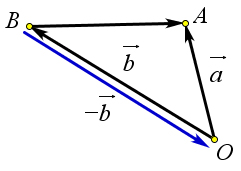
Доказательство.

􏰁→ 􏰁→ 􏰁→ _⃗ 􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→ _⃗ Пусть c⃗ = BA = OA−OB = a⃗−b. По правилу треугольника BA = BO+OA. Кроме того BO = −OB = −b.

_⃗ 􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→
Поэтому a⃗−b=BA=BO+OA=OA+BO=OA+(−OB)=a⃗+(−b).

⃗
Определение 9.16 (о произведении вектора на число). Произведением вектора a⃗ ≠ 0^⃗ на число x ≠ 0

1. ∣x⋅a⃗∣=∣x∣⋅∣a⃗∣

2. он сонаправлен с вектором a⃗, если x > 0, и противоположно направлен вектору a⃗, если x < 0 Если же a⃗=^⃗0 или x=0, то вектор xa⃗=0^⃗ (рис. 146)

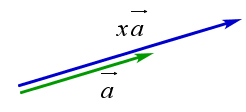
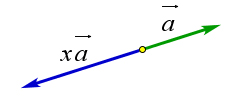
Следствие.

1. 1 ⋅ a⃗ = a⃗ для любого вектора a⃗.
2. (−1)a⃗ = −a⃗ для любого вектора a⃗. 3. Если xa⃗=x^⃗b и x≠0, то a⃗=^⃗b.
4. Если xa⃗=ya⃗ и a⃗≠0^⃗, то x=y.

Доказательство.

a) x > 0.

b) x < 0.

Рис. 147. Определение 9.16.

• По определению вектор 1 ⋅ a⃗ по модулю равен 1 ⋅ ∣a⃗∣ = ∣a⃗∣, кроме того он сонаправлен с a⃗, так как 1 > 0.

• По определению вектор 1⋅a⃗ по модулю равен ∣−1∣⋅∣a⃗∣ = ∣a⃗∣, кроме того он противоположнонаправлен с a⃗, так как −1 < 0, следовательно, это вектор −a⃗.

• Еслиxa⃗=x^⃗b,то∣x∣⋅∣a⃗∣=∣x∣⋅∣^⃗b∣,итаккакx≠0,то∣a⃗∣=∣^⃗b∣.Крометого,еслиx>0,товектораa⃗и^⃗b сонаправлены с a⃗, а если x < 0, то они сонаправлены с −a⃗. Таким образом a⃗ = ^⃗b.

• Если xa⃗ = ya⃗, то ∣x∣ ⋅ ∣a⃗∣ = ∣y∣ ⋅ ∣a⃗∣, а так как a⃗ ≠ ^⃗0, то на ∣a⃗∣ можно сократить, следовательно, ∣x∣ = ∣y∣. А так как вектора xa⃗ ya⃗, то числа x и y одного знака. Следовательно, x = y. 
Теорема 9.2.6 (Характеристическое свойство коллинеарных векторов). Вектор ^⃗b коллинеарен нену- левому вектору a⃗ тогда и только тогда, когда ^⃗b = xa⃗. 
Если ^⃗b = xa⃗, то векторы a⃗ и ^⃗b коллинеарны по определению умножения вектора на число.

1. ^⃗b ⇈ a⃗, тогда x = ^∣⃗b∣ . Действительно, вектор xa⃗ будет сонаправлен с ^⃗b, так как x > 0, кроме того ∣a⃗∣ 
∣xa⃗∣ = ^∣⃗b∣ ⋅ ∣a⃗∣ = ∣^⃗b∣. Следовательно, ^⃗b = xa⃗. ∣a⃗∣

2. ^⃗b 􏰀 a⃗, тогда аналогично первому случаю x = − ^∣⃗b∣ . ∣a⃗∣

Следствие 9.2.6.1. Два вектора, отложенные от одной и той же точки, лежат на одной прямой тогда и только тогда, когда один из них получается из другого умножением на число.

Доказательство.

Теперь докажем, что если ^⃗b ∥ a⃗, то найдется такое число x, что ^⃗b = xa⃗. Если ^⃗b = 0^⃗, то x = 0. Если же ^⃗b ≠ 0^⃗, то возможны два случая:

Доказательство.

􏰁􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→

Рассмотрим вектора AX и AB. Если точка X лежит на прямой AB, то вектора AX и AB колли- 􏰁􏰁→ 􏰁→

неарны по определению, и, следовательно AX = xAB.

􏰁􏰁→ 􏰁→ 􏰁􏰁→
Обратно, если AX = xAB, то вектора AX и AB коллинеарны, а так как у них есть общая точка A,

то они лежат на одной прямой.

􏰁→

86

Теорема 9.2.7. Для любых чисел k,l и любых векторов a⃗,^⃗b справедливы равенства: 1. (kl)a⃗ = k(la⃗);
2. (k+l)a⃗=ka⃗+la⃗;
3. k(a⃗+^⃗b)=ka⃗+k^⃗b.

Доказательство.

1. Докажем, что для любых чисел k, l и любого вектора a⃗ справедливо равенство (kl)a⃗ = k(la⃗). Если a⃗ = 0^⃗, то справедливость этого равенство очевидна. Пусть a ≠ 0. Имеем: ∣(lk)a⃗∣ = ∣kl∣∣a⃗∣ = ∣k∣∣l∣∣a⃗∣ = ∣k∣∣la⃗∣ = ∣k(la⃗)∣. 
Далее, если kl ⩾ 0, то (kl)a⃗ ⇈ a⃗ и k(la⃗) ⇈ a⃗; если же kl < 0, то (kl)a⃗ 􏰀 a⃗ и k(la⃗) 􏰀 a⃗. И в том и в другом случае (kl)a⃗ ⇈ k(la⃗). Следовательно, (kl)a⃗ = k(la⃗).

2. Докажем, что для любого числа k и любых векторов a⃗ и ^⃗b справедливо равенство k(a⃗+^⃗b) = ka⃗+k^⃗b. Если k = 0, или a⃗ = 0^⃗, или ^⃗b = 0^⃗, то справедливость этого равенства очевидна. Пусть k ≠ 0, a⃗ ≠ ^⃗0, ^⃗b ≠ 0^⃗.

Возможны три случая.
(a) a⃗ ⇈ ^⃗b. Тогда вектора k(a⃗ + ^⃗b), ka⃗, k^⃗b, а следовательно, и ka⃗ + k^⃗b, сонаправлены. Кроме того

∣k(a⃗ + ^⃗b)∣ = ∣k∣(∣a⃗∣ + ∣^⃗b∣) = ∣ka⃗∣ + ∣k^⃗b∣ = ∣ka⃗ + k^⃗b∣. Следовательно, k(a⃗ + ^⃗b) = ka⃗ + k^⃗b.

(b) a⃗ 􏰀 ^⃗b. Пусть для определённости ∣a⃗∣ ⩾ ∣^⃗b∣. Тогда и ∣ka⃗∣ ⩾ ∣k^⃗b∣. Тогда k(a⃗ + ^⃗b) ⇈ (ka⃗ + k^⃗b). Кроме того в этом случае ∣k(a⃗+^⃗b)∣ = ∣k∣(∣a⃗∣−∣^⃗b∣) = ∣ka⃗∣−∣k^⃗b∣ = ∣ka⃗+k^⃗b∣. Следовательно, k(a⃗+^⃗b) = ka⃗+k^⃗b.

_⃗ 􏰁􏰁→ 􏰁→
(c) a⃗ ∥/ b. Тогда отложим от какой-нибудь точки O векторы OA₁ = a⃗ и OA = ka⃗, а от точек A₁

􏰁􏰁􏰁→ _⃗ 􏰁→ _⃗
и A векторы A₁B₁ = b и AB = kb. Треугольники OA₁B₁ и OAB подобны с коэффициентом

􏰁→ 􏰁􏰁→ подобия ∣k∣ по второму признаку подобия треугольников. Следовательно, OB = k ⋅ OB₁ =

_⃗ 􏰁→􏰁→􏰁→_⃗⃗⃗ k(a⃗ + b). C другой стороны, OB = OA + AB = ka⃗ + kb. Итак, k(a⃗ + b) = ka⃗ + kb.

3. Докажем, что для любых чисел k, l и любого вектора a⃗ справедливо равенство (k + l)a⃗ = ka⃗ + la⃗.

Если k = l = 0, то справедливость этого равенство очевидна. Пусть хотя бы одно из чисел k,l

отлично от нуля. Для определённости будем считать, что ∣k∣ ⩾ ∣l∣, и, следовательно, k ≠ 0 и ∣ ^l ∣ ⩽ 1. k

Рассмотримвекторa⃗+ ^la⃗.Очевидно,(a⃗+ ^la⃗)⇈a⃗.Далее,∣a⃗+ ^la⃗∣=∣a⃗∣+ ^l∣a⃗∣=(1+ ^l)a⃗.Умножая kkkkk

обе части этого равенства на k, получим, что справедливо равенство ka⃗ + la⃗ = (k + l)a⃗.

Теорема 9.2.8 (теорема «α − β»). Если точка C лежит на отрезке AB, и AC ∶ CB = α ∶ β, то

􏰁→ 􏰁→ 􏰁→

OC= ^α OB+ ^β OA. α+β α+β

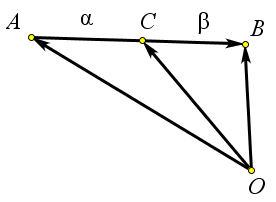
Рис. 148. Теорема 9.2.8.
Доказательство. _􏰁→ ⃗ _{􏰁→ 􏰁→ 􏰁→} ⃗

Выберем произвольную точку O и обозначим a⃗ = OA, b = OB, c⃗ = OC (рис. 148). Тогда AB = b − a⃗,

􏰁→ 􏰁→ _⃗ 􏰁→􏰁→􏰁→ _⃗ ⃗ ⃗ _⃗ AC= ^α AB= ^α (b−a⃗).Тогдаc⃗=OC=OA+AC=a⃗+ ^α (b−a⃗)=^{αa⃗+βa⃗+αb−αa⃗} =^βa⃗+αb = ^β a⃗+ ^α b,

α+β α+β
􏰁→ 􏰁→ 􏰁→

α+β α+β α+β α+β α+β

тоестьOC= ^α OB+ ^β OA. α+β α+β

87

9.3 Координаты векторов

Определение 9.17. Линейной комбинацией векторов a⃗ и ^⃗b называется вектор αa⃗ + β^⃗b. Числа α и β называются коэффициентами линейной комбинации.

Лемма 9.3.1. Если вектора a⃗ и ^⃗b неколлинеарны и xa⃗ + y^⃗b = 0^⃗, то x = y = 0. Доказательство. _{⃗ ⃗}

Предположим, что x ≠ 0. Тогда можно выразить a⃗ = − ^y b, откуда следует, что a⃗ ∥ b, что противоречит x

условию. Таким образом x = 0. Аналогично можно доказать, что y = 0.
Теорема 9.3.2 (о разложении вектора на составляющие). Любой вектор можно единственным об-

разом представить в виде линейной комбинации двух наперед заданных неколлинеарных векторов.

Рис. 149. Теорема 9.3.2.

Доказательство.

Пусть a⃗ и ^⃗b – данные неколлинеарные векторы. Докажем, что любой вектор p⃗ можно разложить по векторам a⃗ и ^⃗b. Возможны два случая.

1. Вектор p⃗ коллинеарен одному из векторов a⃗ и ^⃗b, например вектору ^⃗b. В этом случае по теореме 9.2.6 вектор p можно представить в виде p⃗ = y^⃗b, где y – некоторое число, и, следовательно, p⃗ = 0 ⋅ a⃗ + y ⋅ ^⃗b, то есть вектор p⃗ разложен по векторам a⃗ и ^⃗b.

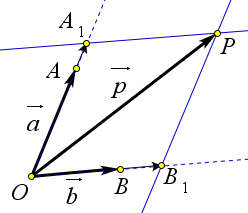
2. Вектор p⃗ не коллинеарен ни вектору a⃗, ни вектору ^⃗b (рис. 149). Отметим какую-нибудь точку O и 􏰁→ 􏰁→_⃗􏰁→

отложим от неё векторы OA = a⃗, OB = b, OP = p⃗. Через точку P проведём прямую, параллельную

прямой OB, и обозначим через A₁ точку пересечения этой прямой с прямой OA. По правилу 􏰁􏰁→ 􏰁􏰁→ 􏰁􏰁→ 􏰁􏰁→

треугольника p⃗ = OA₁ + A₁P . Но векторы OA₁ и A₁P коллинеарны соответственно векторам a⃗ и _⃗ 􏰁􏰁→ 􏰁􏰁→ _{⃗ ⃗}
b, поэтому существуют числа x и y, такие, что OA₁ = xa⃗, A₁P = yb. Следовательно, p⃗ = xa⃗ + yb, то

есть вектор p⃗ разложен по векторам a⃗ и ^⃗b.

Докажем теперь, что коэффициенты x и y разложения определяются единственным образом.

Допустим, что наряду с разложением p⃗ = xa⃗ + y^⃗b имеет место разложение p⃗ = x₁a⃗ + y₁^⃗b. Вычитая

второе равенство из первого и используя правила действий над векторами, получаем 0^⃗ = (x −

x₁)a⃗+(y−y₁)^⃗b. Но это равенство может выполняться, только если x−x₁ = y−y₁ = 0. В самом деле,

если предположить, что например x − x₁ ≠ 0, то из полученного равенства найдем a⃗ = − ^{y−y1 ⃗}b, _⃗ x−x₁

а значит, векторы a⃗ и b коллинеарны. Но это противоречит условию теоремы. Следовательно, x−x₁ = 0 и y−y₁ = 0. Откуда x = x₁ и y = y₁. Это и означает, что коэффициенты разложения вектора p⃗ определяются единственным образом.

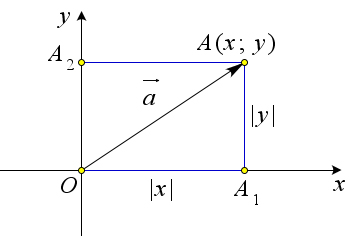
Определение 9.18. Пусть прямая Oy ∥ ^⃗j, а прямая Ox ∥ ^⃗i, кроме того Oy ⊥ Ox, и ^⃗i ⊥ ^⃗j, ∣^⃗i∣ = ∣^⃗j∣ = 1 (рис. 150). Тогда говорят, что на плоскости xOy задана прямоугольная система координат, а коэффициенты разложения произвольного вектора a⃗ по базису (^⃗i, ^⃗j) называются координатами вектора a⃗ в этой системе координат. Вектора ^⃗i и ^⃗j называют координатными ортами.

88

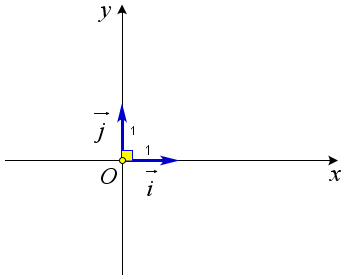
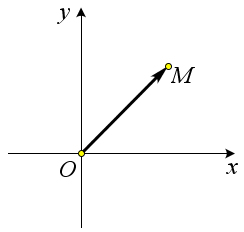
Рис. 150. Определение 9.18.
Определение 9.19. Радиус-вектором точки M в системе координат xOy называют вектор OM (рис.

151)

1. Два вектора равны тогда и только тогда, когда их координаты соответственно равны. 2. При сложении векторов их соответствующие координаты складываются.
3. При умножении вектора на число его координаты умножаются на это число.

Доказательство.

1. Пустьa⃗=^⃗b,a⃗=x^⃗i+y^⃗j,^⃗b=x₁^⃗i+y₁^⃗j.Тогдаx^⃗i+y^⃗j=x₁^⃗i+y₁^⃗jили(x−x₁)^⃗i+(y−y₁)^⃗j=0.Таккак ^⃗i∥/^⃗j,тополемме9.3.1x−x₁ =y−y₁ =0,тоестьx=x₁ иy=y₁.

Обратно, если a⃗ = x^⃗i + y^⃗j, и ^⃗b = x^⃗i + y^⃗j, то очевидно a⃗ = ^⃗b.

2. Рассмотрим вектора a⃗(x₁; y₁) и ^⃗b(x₂; y₂). Так как a⃗ = x₁^⃗i + y₁^⃗j и ^⃗b = x₂^⃗i + y₂^⃗j то, пользуясь свойствами сложения векторов и умножения вектора на число, получим: a⃗+^⃗b = x₁^⃗i+y₁^⃗j+x₂^⃗i+y₂^⃗j = (x₁ + x₂)^⃗i + (y₁ + y₂)^⃗j. Отсюда следует, что координаты вектора a⃗ + ^⃗b равны (x₁ + x₂; y₁ + y₂).

3. Пусть вектор a⃗ имеет координаты (x; y). Тогда вектор ka⃗ = k(x^⃗i + y^⃗j) = kx^⃗i + ky^⃗j, то есть коорди- наты вектора ka⃗ равны (kx;ky).

Теорема 9.3.4. Координаты радиус-вектора совпадают с координатами его конца.

􏰁􏰁→

Теорема 9.3.3.

Рис. 151. Определение 9.19.

a)

b)

Рис. 152. Теорема 9.3.4.

89

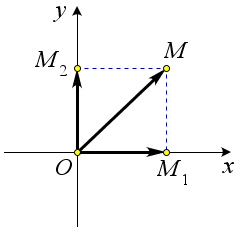
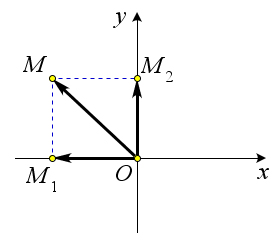
Доказательство.

􏰁􏰁→ 􏰁􏰁→ 􏰁􏰁→ 􏰁􏰁→ _⃗ 􏰁􏰁→ _⃗
Пусть OM = OM₁ +OM₂. Докажем, что OM₁ = xi и OM₂ = yj. В самом деле, если x > 0 (рис. 152 a),

􏰁􏰁→ _⃗ 􏰁􏰁→ _{⃗ ⃗}
то x = ∣OM₁∣, а векторы OM₁ и i сонаправлены. Поэтому OM₁ = ∣OM₁∣⋅i = xi. Если x < 0 (рис. 152 b), то

􏰁􏰁→ _⃗ 􏰁􏰁→ _{⃗ ⃗}
x = −∣OM₁∣, а векторы OM₁ и i противоположно направлены. Поэтому OM₁ = −∣OM₁∣i = xi. Наконец,

􏰁􏰁→ _⃗ 􏰁􏰁→ _⃗
если x = 0, то OM₁ = 0 и равенство OM₁ = xi в этом случае также справедливо. Таким образом, в любом

􏰁􏰁→ _⃗ 􏰁􏰁→ _⃗ 􏰁􏰁→ 􏰁􏰁→ 􏰁􏰁→ _{⃗ ⃗} случае OM₁ = xi. Аналогично доказывается, что OM₂ = yj. Следовательно, OM = OM₁ + OM₂ = xi + yj.

􏰁􏰁→
Отсюда следует, что координаты радиус-вектора OM равны (x;y), то есть равны соответствующим

координатам точки M.

Теорема 9.3.5 (Связь координат векторов и координат его начала и конца). Координаты вектора 􏰁→
AB равны разностям соответствующих координат точек B и A.

Рис. 153. Теорема 9.3.5.

Доказательство.

Пусть точка A имеет координаты (x₁;y₁), а точка B имеет координаты (x₂;y₂) (рис. 153). Тогда 􏰁→ 􏰁→ 􏰁→
AB = OB − OA = (x₂; y₂) − (x₁; y₁) = (x₂ − x₁; y₂ − y₁).

Теорема 9.3.6 (о модуле вектора). Для любого вектора a⃗(x ; y ) его модуль вычисляется по формуле

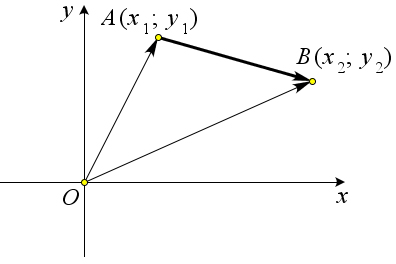
∣ a⃗ ∣ =

√

x ²₁ + y ₁² .

11

Рис. 154. Теорема 9.3.6.

Доказательство.

_􏰁→Если x = 0 или y = 0, то формула очевидна. Пусть x ≠ 0 и y ≠ 0. Отложим от начала координат вектор

OA = a⃗ и проведем через точку A перпендикуляры AA₁ и AA₂ к осям Ox и Oy (рис. 154). Координаты 􏰁→

точки A равны координатам вектора OA, то есть (x;y). Поэтому ∣OA ∣ = ∣x∣,∣AA ∣ = ∣OA ∣ = ∣y∣. По √√¹√¹²

теореме Пифагора ∣OA∣ = ∣OA₁∣² + ∣AA₁∣² = x² + y². Таким образом ∣a⃗∣ = x² + y².
Теорема 9.3.7 (формула расстояния между двумя точками). Если A(x ;y ) и B(x ;y ), то ∣AB∣ =

√

11 22

(x₁ −x₂)² +(y₁ −y₂)². Доказательство.

􏰁→
Если A(x ;y ) и B(x ;y ), то вектор AB имеет координаты (x −x ;y −y ). Следовательно, ∣AB∣ =

√
Теорема 9.3.8 (координаты середины отрезка). Если A(x₁;y₁) и B(x₂;y₂), то точка M середина

􏰁→ ∣AB∣=

11 22 2121 (x₁ −x₂)² +(y₁ −y₂)².

отрезка AB имеет координаты M(^x1+x2 ; ^y1+y2 ). 22

90

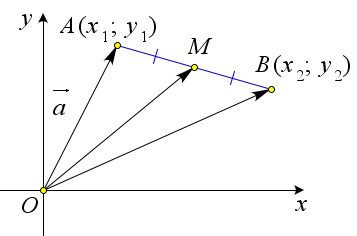
Рис. 155. Теорема 9.3.8.

^{Доказательство.} _{􏰁􏰁→ 􏰁→ 􏰁→ 􏰁􏰁→} 􏰁→ 􏰁􏰁→
По теореме 9.2.8 OM = ¹ OA + ¹ OB (рис. 155). Таким образом OM = ^OA+OB = ^{(x1 ;y1 )+(x2 ;y2 )} =

^{(x1+x2;y1+y2)} = (^x1+x2 ; ^y1+y2 ). Таким образом точка M имеет координаты (^x1+x2 ; ^y1+y2 ). 222 22

9.4 Скалярное умножение векторов

Определение 9.20. Углом между двумя ненулевыми векторами называется величина образуемого ими угла, когда они отложены от одной точки.

Определение 9.21. Скалярным произведением двух векторов называется произведение их модулей и косинуса угла между ними. Если хотя бы один из векторов нулевой, то их скалярное произведение полагают равным нулю.

Определение 9.22. Скалярным квадратом вектора называется его произведение самого на себя. Теорема 9.4.1. Для любых двух ненулевых векторов их скалярное произведение равно нулю тогда и

только тогда, когда они перпендикулярны. Доказательство. _⃗

Пусть α = _∠(a⃗; b).

1. Если α=90^○, то cosα=0, следовательно a⃗⋅^⃗b=∣a⃗∣∣^⃗b∣cosα=0.

2. Если a⃗⋅^⃗b = 0, то ∣a⃗∣∣^⃗b∣cosα = 0. Но поскольку ∣a⃗∣ ≠ 0 и ∣^⃗b∣ ≠ 0 по условию, то cosα = 0. А значит, α = 90^○.

Теорема 9.4.2 (скалярное произведение в координатах). Скалярное произведение двух векторов равно сумме произведений их соответствующих координат.

2222

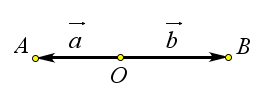
a)

b) c) Рис. 156. Теорема 9.4.2.

Доказательство. _⃗

Если хотя бы один из векторов a⃗ или b нулевой, то справедливость теоремы очевидна. Рассмотрим _⃗ 􏰁→ 􏰁→_⃗

случай, когда векторы a⃗ и b ненулевые. Отложим от произвольной точки O векторы OA = a⃗ и OB = b. Пусть α = _∠(a⃗; ^⃗b). Если векторы a⃗ и ^⃗b не коллинеарны (рис. 156 a), то по теореме косинусов

AB² =OA² +OB² −2OA⋅OBcosα. (1)

Это равенство верно и в том случае, если векторы a⃗ и ^⃗b коллинеарны. Действительно, если a⃗ ⇈ ^⃗b (рис. 156 b), то AB² = (OA−OB)² = OA² +OB² −2OA⋅OB = OA² +OB² −2OA⋅OBcos0^○ = OA² + OB² −2OA⋅OBcosα. Если же a 􏰀 b (рис. 156 c), то AB² = (OA+OB)² = OA² +OB² +2OA⋅OB = OA² +OB² −2OA⋅OBcos180^○ =OA² +OB² −2OA⋅OBcosα.

91

^􏰁→_⃗^{􏰁→􏰁→}_{⃗ ⃗}22_⃗2 _⃗ ТаккакAB=b−a⃗,OA=a⃗,OB=b,торавенство(1)можнозаписатьтак:∣a⃗−b∣ =∣a⃗∣ +∣b∣−2a⃗⋅b,

откуда

a⃗⋅^⃗b= ¹(∣a⃗∣² +∣^⃗b∣² −∣a⃗−^⃗b∣²). (2) 2

x² +y₂,∣^⃗b−a⃗∣² = (x₂ −x₁)² +(y₂ −y₁)². Подставив эти выражения в правую часть равенства (2), получим

Теорема 9.4.3 (Свойства скалярного произведения).

• 1^○  a⃗ ⋅ ^⃗b = ^⃗b ⋅ a⃗ ;

• 2^○  ( k a⃗ ) ⋅ ^⃗b = k ( a⃗ ⋅ ^⃗b ) ;

• 3^○  ( a⃗ + ^⃗b ) ⋅ c⃗ = a⃗ ⋅ c⃗ + ^⃗b ⋅ c⃗ .

Векторы a⃗,^⃗b и ^⃗b−a⃗ имеют координаты (x₁;y₁),(x₂;y₂) и (x₂ −x₁;y₂ −y₁), поэтому ∣a⃗∣² = x²₁ +y₁²,∣^⃗b∣² =

a⃗⋅^⃗b=¹(x²+y²+x²+y²−x²−x²+2xx −y²−y²+2yy)=xx +yy. ₂112212¹²12¹²¹²¹²

Доказательство. _⃗ Первое свойство очевидно в силу определения скалярного произведения. Действительно, a⃗ ⋅ b = ∣a⃗∣∣^⃗b∣ cos _∠(a⃗; ^⃗b) = ∣^⃗b∣∣a⃗∣ cos _∠(^⃗b; a⃗) = ^⃗b ⋅ a⃗. _⃗ Докажем второе свойство, используя теорему 9.4.2. Пусть a⃗ имеет координаты (x₁;y₁), а вектор b имеет координаты (x₂;y₂). Тогда вектор (ka⃗)⋅^⃗b = (kx₁;ky₁)⋅(x₂;y₂) = kx₁x₂+ky₁y₂ = k(x₁x₂+y₁y₂) = ka⃗⋅^⃗b. Докажем третье свойство, используя теорему 9.4.2. Пусть вектор a имеет координаты (x_a;y_a), век- тор b имеет координаты (x_b ; y_b ), вектор c имеет координаты (x_c ; y_c ). Тогда (a⃗ + ^⃗b) ⋅ c⃗ = (x_a + x_b ; y_a + y_b ) ⋅

(x_c;y_c)=(x_a +x_b)x_c +(y_a +y_b)y_c =x_ax_c +x_bx_c +y_ay_c +y_by_c =(x_ax_c +y_ay_c)+(x_bx_c +y_by_c)=a⃗⋅c⃗+^⃗b⋅c⃗. Теорема 9.4.4 (формулы векторного метода).

1. ∣a⃗∣ = ^√a⃗²;
2. cos∠(a⃗;^⃗b)= ^a⃗⋅⃗b ;

∣a⃗∣∣^⃗b∣ 3. Пр (^⃗b) = ^a⃗⋅⃗b .

^a⃗ ∣a⃗∣

Доказательство.

Докажем первый пункт теоремы. По определению a⃗² = a⃗ ⋅ a⃗ = ∣a⃗∣∣a⃗∣ cos 0^○ = ∣a∣² , то есть a² = ∣a⃗∣² . Взяв корень из обеих частей этого равенства, получаем ∣a⃗∣ = ^√a⃗².

Докажем второй пункт теоремы. По определению a⃗ ⋅ ^⃗b = ∣a⃗∣∣^⃗b∣ cos _∠(a⃗; ^⃗b). Разделив обе части этого равенства на произведение модулей векторов a⃗ и ^⃗b, получим cos _∠(a⃗; ^⃗b) = ^a⃗⋅⃗b .

∣a⃗∣∣^⃗b∣ Докажем третий пункт теоремы. Пр (^⃗b) = ∣^⃗b∣ cos _∠(a⃗; ^⃗b) = ^{∣a⃗∣∣⃗b∣ cos ∠(a⃗;⃗b)} = ^a⃗⋅⃗b .

^a⃗ ∣a⃗∣ ∣a⃗∣
10 Метод координат. Уравнение линий на плоскости

10.1 Уравнение прямой

Теорема 10.1.1 (Различные виды уравнения прямой). Уравнение прямой AB можно записать в следующих формах

􏰁􏰁→ 􏰁→ 􏰁→
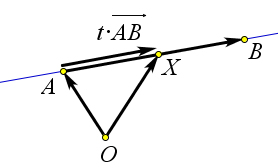
1. Векторное уравнение прямой: OX = OA + t ⋅ AB, где X – переменная точка прямой AB.

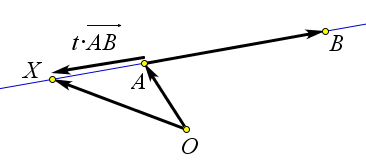
a)

b)
Рис. 157. Теорема 10.1.1 пункты 1 и 2.

c)

92

Доказательство.

􏰁􏰁→ 􏰁→

Пусть X – произвольная точка прямой AB. Тогда вектора AX и AB коллинеарны, и, следо-

􏰁􏰁→ 􏰁→
вательно существует такое число t, что AX = t ⋅ AB. Тогда, взяв произвольную точку O, можно

􏰁􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→ 􏰁→
написать OX = OA+AX = OA+t⋅AB. Таким образом для произвольной точки X прямой AB мож-

􏰁􏰁→ 􏰁→ 􏰁→
но написать уравнение OX = OA+t⋅AB. При этом очевидно, что для каждого числа t существует

единственная точка X, для которой равенство будет верно, и наоборот. 􏰁􏰁→ 􏰁→ 􏰁→

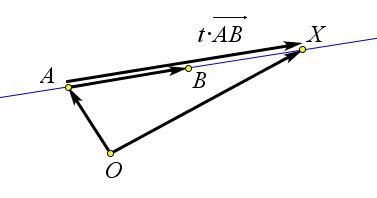
2. OX = (1−t)⋅OA+t⋅OB, где X – переменная точка прямой AB, причем X лежит между точками A и B, если 0<t<1 (рис. 157 b), лежит за точкой B, если t>1 (рис. 157 a), лежит за точкой A, если t < 0 (рис. 157 c), совпадает с точкой A, если t = 0, совпадает с точкой B, если t = 1.

Доказательство.

􏰁􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→ Преобразуем правую часть данного уравнения: OX = (1 − t) ⋅ OA + t ⋅ OB = OA + t ⋅ (OB − OA) =

􏰁→ 􏰁→ 􏰁􏰁→ 􏰁→ 􏰁→ 􏰁→
OA + t ⋅ AB. То есть OX = OA + t ⋅ AB. Тогда, перенеся вектор OA в правую часть и преобразовав

􏰁􏰁→ 􏰁→
разность по правилу треугольника, получим AX = t ⋅ AB. Откуда в силу определения умножения

вектора на число ясно, что точка X лежит между точками A и B, если 0 < t < 1, лежит за точкой B, если t > 1, лежит за точкой A, если t < 0, совпадает с точкой A, если t = 0, совпадает с точкой B, если t=1.

3. Уравнение по направляющему вектору и точке ^x−x0 = ^y−y0 , при условии, что p ≠ 0, q ≠ 0; pq

Рис. 158. Теорема 10.1.1 пункт 3.

Доказательство.

Пусть точка A имеет координаты (x₀;y₀), вектор v имеет координаты (p;q). Пусть произвольная

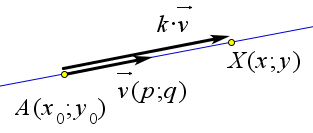
точка X искомой прямой имеет координаты (x;y). Кроме того, так как вектора AX и v колли- 􏰁􏰁→

неарны, то AX =k⋅v⃗, или в координатах (x−x₀;y−y₀)=(kp;kq). Тогда x−x₀ =kp и y−y₀ =kq. Выразив из обоих равенств число k, получим k = ^x−x0 = ^y−y0 , то есть ^x−x0 = ^y−y0 .

pq pq 4. Уравнение по двум точкам ^x−x1 = ^y−y1 , при условии, что y₂ ≠ y₁ и x₂ ≠ x₁.

x₂ −x₁ y₂ −y₁

Доказательство.

Таким образом положив в уравнении прямой по точке и направляющему вектору p = x₂ − x₁ , q =

y₂−y₁,x₀=x₁,y₀=y₁,получим^x−x1 =^y−y1. x₂ −x₁ y₂ −y₁

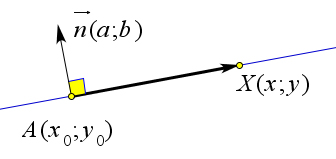
5. Уравнение по нормали и точке: a(x − x₀) + b(y − y₀) = 0.

Рис. 159. Теорема 10.1.1 пункт 5.

Если точка A имеет координаты (x₁;y₁), а точка B имеет координаты (x₂;y₂), то в качестве 􏰁→

направляющего вектора прямой AB можно взять вектор AB с координатами (x₂ −x₁;y₂ −y₁).

93

Доказательство.

Пусть вектор n с координатами (a;b) является нормалью к прямой l, проходящей через точку 􏰁􏰁→

A(x₀;y₀). Тогда для любой точки X данной прямой AX будет перпендикулярен n⃗, следовательно 􏰁􏰁→
AX ⋅ n⃗ = 0. Расписав это равенство в координатах, получим a(x − x₀) + b(y − y₀) = 0.

6. Общее уравнение прямой: ax + by + c = 0. Доказательство. 
Раскроем скобки в правой части уравнения прямой по нормали и точке: a(x − x₀) + b(y − y₀) = ax−ax₀+by−by₀ =ax+by+(−ax₀+by₀).Такимобразомуравнениепрямойможнозаписатьввиде ax+by+(−ax₀ −by₀)=0. Обозначив c=−ax₀ −by₀, получим уравнение ax+by+c=0, где (a;b) – нормаль к данной прямой.

7. Уравнение прямой с угловым коэффициентом: y = kx + b. Доказательство. 
Пусть прямая задана общим уравнением Ax + By + C = 0, причём A ≠ 0 (коэффициенты A, B и C 
обозначены большими буквами, чтобы не было накладки обозначений). Тогда можно выразить 
y = − ^B x − ^C . Обозначив k = − ^B , b = − ^C , получим y = kx + b. AAAA

Теорема 10.1.2. Коэффициент k в уравнение прямой с угловым коэффициентом равен тангенсу угла наклона прямой к оси OX.

Рис. 160. Теорема 10.1.2.

Доказательство.

n⃗ к данной прямой имеет координаты (A,B) (рис. 160). Тогда вектор v(B;−A) будет направляющим вектором данной прямой, так как n ⋅ v = A ⋅ B + B ⋅ (−A) = 0. Тангенс угла наклона направляющего вектора равен тангенсу угла наклона прямой, вне зависимости от выбора направляющего вектора, так как tg (180^○ − φ) = tg φ. Тангенс угла наклона вектора v(B; −A) очевидно равен tg φ = ^B = − ^B .

кости прямую.

Доказательство.

Пусть на плоскости введены прямоугольные координаты x, y и задано линейное уравнение ax+by+c = 0. Покажем, что это уравнение задаёт прямую.

Если b = 0, то a ≠ 0 (иначе уравнение не будет линейным). Тогда данное уравнение можно записать так: x = − ^c . Это уравнение прямой, перпендикулярной оси Ox.

a

Пусть теперь b ≠ 0. построим прямую, перпендикулярную вектору n⃗(a; b), проходящую через точку (0; − ^c ). Очевидно, эта прямая задаётся уравнением ax + by + c = 0.

b

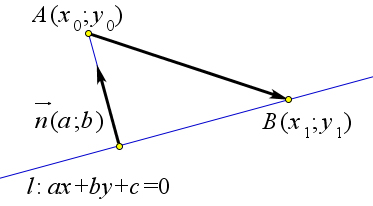
Теорема 10.1.4. Расстояние от точки A(x₀;y₀) до прямой l ∶ ax+by+c = 0 выражается по формуле

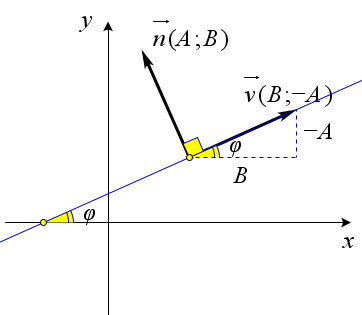
Из вывода уравнения прямой с угловым коэффициентом следует, что k = − ^B , где вектор нормали A

−A A Теорема 10.1.3. Каждое линейное уравнение в прямоугольной системе координат задает на плос-

ρ(A;l)= ^√

∣ax₀ +b₀ +c∣

.

a² +b²

94

Доказательство.

Рис. 161. Теорема 10.1.4.

Рассмотрим произвольную точку B(x₁;y₁) прямой l (рис. 161). Вектор n⃗(a;b) является нормалью 􏰁→ 􏰁→ ^􏰁→

∣n⃗ ⋅AB ∣ ∣(x₁ −x₀ ;y₁ −y₀ )⋅(a;b)∣
к прямой l. Тогда ρ(A; l) = Пр (AB). По пункту 3 теоремы 9.4.4 Пр (AB) = = ^√ =

^{n⃗ n⃗} ∣ n⃗ ∣ _a 2 _{+ b} 2

.ТаккакточкаB(x;y)лежитнапрямойl,тоax +by +c=0,то 11 11

=

∣+ax₀ +by₀ +c∣
^√ _{2 2} . Модуль в числителе необходим, чтобы выражение было положительным вне зависимости

a +b
от выбора направления нормали к прямой.

10.2 Кривые второго порядка

10.2.1 Окружность
Теорема 10.2.1. Уравнение окружности с центром в точке O(a;b) и радиусом R имеет вид (x−

√ ₌ √ a² +b²

∣x₁ a−x₀ a+y₁ b−y₀ b∣ ∣−x₀ a−y₀ b+x₁ a+y₁ b∣

a² +b²
есть ax + by = −c. Подставив это выражение в последнее равенство, получим: ρ(A; l) = ^√

11

∣−ax₀ −by₀ −c∣ a² +b²

a)² + (y − b)² = R².

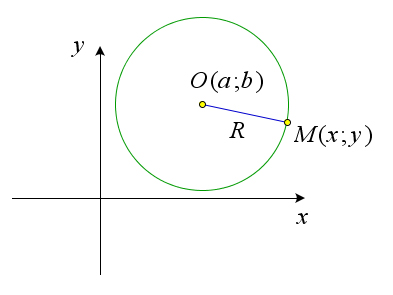
Доказательство.

Рис. 162. Теорема 10.2.1.

Пусть M(x;y) – это произвольная точка данной окружности (рис. 162). По определению окружности OM = R. Воспользовавшись формулой расстояния между двумя точками, получим ^√(x−a)² +(y−b)² =R или (x−a)² +(y−b)² =R².

10.2.2 Парабола

Определение 10.1. Парабола – это геометрическое место точек, равноудаленных от данной прямой и данной точки, не лежащей на этой прямой. Прямая называется директрисой, а точка – фокусом параболы.

Теорема 10.2.2. Каноническое уравнение параболы имеет вид y² = 2px. При этом уравнение дирек-

трисы x = −^p, фокус F(^p;0). 22

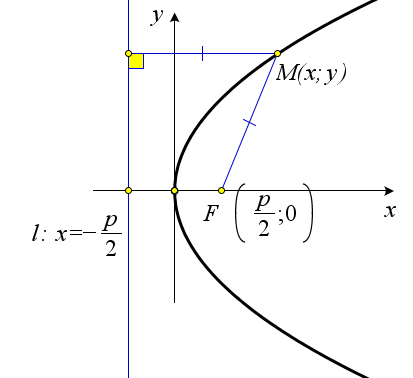
Рис. 163. Теорема 10.2.2.

95

Доказательство.

Пусть точка F ( ^p ; 0) – это фокус параболы, а прямая l с уравнением x = − ^p – это её директриса. 22

Пусть точка M(x;y) – это произвольная точка параболы (рис. 163). Тогда по определению MF = ρ(M;l).Используяформулурасстояниямеждудвумяточками,получим^√(x−^p)²+y² =x+^p.Возведя

22
обе части этого уравнения в квадрат, раскрыв скобки и сократив подобные слагаемые, получим y² =

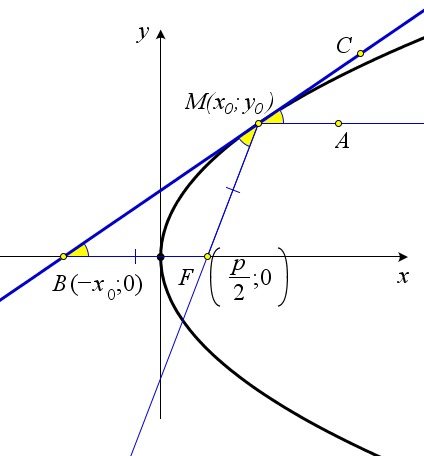
2px.
Теорема 10.2.3 (касательная к параболе). Пусть точка M₀(x₀;y₀) – произвольная точка параболы.

y² = 2px. Тогда уравнение касательной к параболе, проведенной в этой точке имеет вид yy₀ = p(x+x₀).

Рис. 164. Теорема 10.2.3.

Доказательство.

По определению касательной к кривой в данной токе M называется предельное положение се- кущей M₀M₁ при условии, что точка M₁ стремится к точке M₀ по данной кривой. Рассмотрим уравнение секущей к параболе, проходящей через точку M₀(x₀;y₀) и не совпадающую с ней точ-

ку M₁(x₁;y₁) (рис. 164). Так как обе точки лежат на параболе y² = 2px, то их координаты мож-

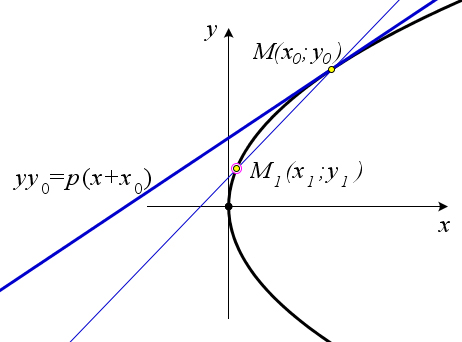
y₀²
₌ y−y_{0 ,} ^x−2p ₌

то y₁ стремиться к y₀. Тогда последнее равенство можно записать в виде 2px − y₀² = (y − y₀) ⋅ 2y₀ или

2px−y² = 2yy −2y²,2px+y² = 2yy . А так как y² = 2px , то получаем уравнение 2px+2px = 2yy или 00000 00 00

p(x + x₀) = yy₀.
Теорема 10.2.4 (Оптические свойства параболы).

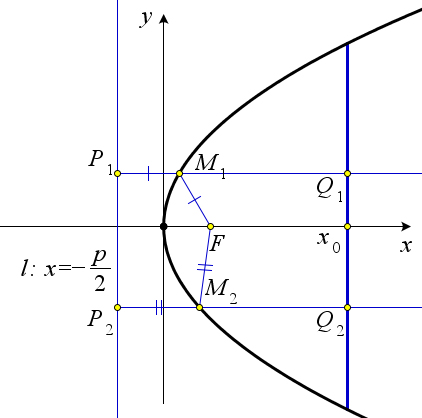
1. Любой луч света, исходящий из фокуса параболы, после отражения от параболы становится параллельным оси параболы.

2. Если источник света помещен в фокусе параболы, то фронт отраженной от параболы волны представляет собой отрезок, соединяющий две точки параболы и параллельный ее директрисе.

22
но записать в виде M (^y0 ;y ),M (^y1 ;y ). Запишем уравнение прямой M M : ^x−x0

⁰ 2p ^{0 1} 2p ^{1 0 1} x₀−x₁
^y−y0 , ^2px−y02 = ^y−y0 ,2px − y² = (y − y )(y + y ). Если точка M стремиться к точке M по параболе,

y₀−y₁ y₀²−y₁² y₀−y₁ ^{0 0 0 1 1 0}

y₀−y₁ ^y₀^{2 y}₁² 2p ⁻ 2p

Доказательство.

a)

b)

Рис. 165. Теорема 10.2.4.

Рассмотрим каноническую параболу y² = 2px. Пусть F ( ^p ; 0) – это фокус параболы, а точка 2

M(x₀;y₀) произвольная точка данной параболы. Пусть луч света FM, отразившись от параболы пе- реходит в луч MA. Кроме того, пусть B – это точка пересечения оси Ox с касательной к параболе, проведенной в точке M (рис. 165 a). По свойству отражения луча света _∠BMF = _∠CMF. Докажем,

96

что треугольник BMF – равнобедренный. Так как ордината точки B равна нулю, то из уравнения касательной yy = p(x + x ) легко найти, что абсцисса точки B равна −x . По формуле расстояния

^{0 0} √ √ ⁰√ междудвумяточками,имеем:MF= (x₀−^p)²+y₀= (x₀−^p)²+2px₀= (x₀+^p)²=x₀+^p=BF.

2222

Таким образом _∠FBM = _∠FMB, следовательно, _∠FBM = _∠CMF. А так как эти углы являются соответственными, то прямые MA и BF параллельны.

Докажем второй пункт теоремы. Необходимо доказать, что вне зависимости от выбора точки на параболе сумма расстояний от неё до фокуса и до выбранного фронта будет постоянна. Пусть фронт волны изображается прямой x = x₀ (рис. 165 b). Докажем, что для точек M₁ и M₂ будет выполнено FM₁ +M₁Q₁ = FM₂ +M₂Q₂. По первому пункту теоремы лучи M₁Q₁ и M₂Q₂ параллельны оси парабо- лы, следовательно, они перпендикулярны директрисе. Тогда по определению параболы FM₁ = M₁P и FM₂ = M₂P₂. Тогда FM₁+M₁Q₁ = P₁M₁+M₁Q₁ = P₁Q₁ = x₀+^p = P₂Q₂ = P₂M₂+M₂Q₂ = M₂F+M₂Q₂.

2

10.2.3 Эллипс
Определение 10.2. Эллипс – это геометрическое место точек, сумма расстояний от которых до двух

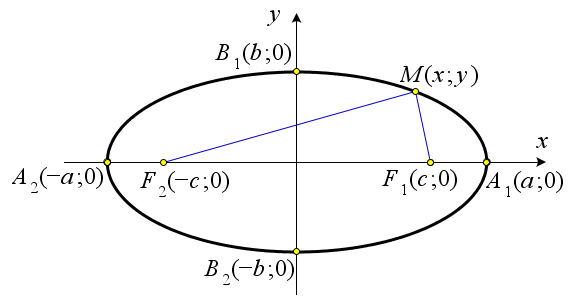
данных точек F₁ и F₂ постоянна и при этом больше, чем ∣F₁F₂∣. Теорема 10.2.5. Каноническое уравнение эллипса имеет вид ^x2 + ^y2

= 1, число a называется большой

полуосью эллипса, b – малой полуосью, a > b.

a² b²

Доказательство.

Рис. 166. Теорема 10.2.5.

Пусть M(x,y) – это произвольная точка, принадлежащая данному эллипсу, а точки F₁(c;0) и F₂(−c;0) – это его фокусы (рис. 166). Тогда по определению эллипса сумма MF₁ +MF₂ постоянна. Пусть эта сумма равна 2a, то есть M F₁ + M F₂ = 2a. Распишем это равенство с помощью формулы расстояния между двумя точками:

^√(x−c)² +y² +^√(x+c)² +y² =2a
. Возведём это равенство в квадрат, раскроем скобки и приведём подобные слагаемые:

2x² +2c² +2y² +2^√(x−c)² +y^2√(x+c)² +y² =4a^{2 √}(x−c)² +y^2√(x+c)² +y² =2a² −(x² +y² +c²).

или
При условии, что 2a² − (x² + y² + c²) ⩾ 0, данное уравнение можно возвести в квадрат:

или

((x−c)² +y²)((x+c)² +y²)=4a⁴ −4a²(x² +y² +c²)+(x² +y² +c²)²
(x² +c² +y² −2xc)(x² +c² +y² +2xc)=4a⁴ −4a²x² −4a²y² −4a²c² +(x² +y² +c²)².

В левой части раскроем скобки, используя формулу разности квадратов:

(x² +y² +c²)² −4x²c² =4a⁴ −2a²x² −2a²y² −2a²c² +(x² +y² +c²)².
Сократив подобные слагаемые, перенеся все слагаемые в одну часть, и сократив на 4, получим:

Перегруппируем слагаемые:

a⁴ −a²x² −a²y² −a²c² +x²c² =0. (a⁴ −a²c²)+(x²c² −x²a²)−a²y² =0,

x²(a² − c²) + a²y² = a²(a² − c²) 97

. Так как a > c, то можно разделить последнее равенство на a²(a² − c²): ^x2+ ^y2 =1.

a² a² − c^2
x2 + ^y2 = 1. (1)

Обозначив b² = a² − c², получим
Теперь докажем, что любая пара чисел (x,y), удовлетворяющая последнему равенству, удовлетво-

a² b²
ряет условию 2a² − (x² + y² + c²) ⩾ 0. Преобразуем левую часть:

2a² −(x² +y² +c²)=a² +(a² −c²)−x² −y² =a² +b² −x² −y². Изравенства1следует,чтоx² =a²(1−^y2)⩽a²,таккак1−^y2 ⩽1.Аналогичноx² =b²(1−^x2)⩽b².

Следовательно, x² ⩽ a², y² ⩽ b², а значит, или

Следовательно,

2a² −(x² +y² +c²)⩾0.

b² b² a²

x² + y² ⩽ a² + b² a² + b² − x² − y² ⩾ 0.

Замечание (свойства канонического эллипса).

1. Вершины эллипса имеют координаты A_1,2(±a;0) и B_1,2(0;±b).

2. Фокусы канонической эллипса имеют координаты F₁ (c; 0) и F₂ (−c; 0), при этом b² = a² − c² и a > c.

3. Эксцентриситетом эллипса называется число e = ^c . a

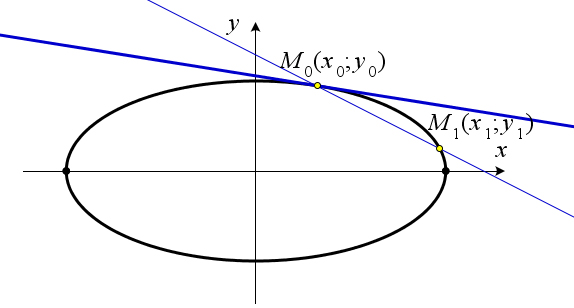
Теорема 10.2.6 (касательная к эллипсу). Пусть точка M(x₀;y₀) – произвольная точка эллипса. ^x2 + ^y2 = 1. Тогда уравнение касательной к эллипсу, проведенной в этой точке имеет вид ^xx0 + ^yy0 = 1.

a² b²

a² b²

Доказательство.

Рис. 167. Теорема 10.2.6.

По определению касательной к кривой в данной токе M называется предельное положение секущей M₀M₁ при условии, что точка M₁ стремится к точке M₀ по данной кривой. Рассмотрим уравнение секущей к эллипсу, проходящей через точку M₀(x₀;y₀) и не совпадающую с ней точку M₁(x₁;y₁) (рис. 167). Поскольку точка M₁ стремиться к точке M₀, можно считать, что знаки их соответствующих координат совпадают (если одна из координат точки M₀ равна 0, то соответствующую координату точки M₁ будем брать с каким-либо определённым знаком). Рассмотрим случай, когда абсциссы точек

M и M неотрицательны. Так как обе точки лежат на эллипсе ^x2 + ^y2 = 1, то их координаты можно ⁰¹ _{√ √} a²b²

записать в виде M₀(^a b² −y²;y₀),M₁(^a b² −y²;y₁). Запишем уравнение прямой M₀M₁: b⁰b¹

x−x_{0 =}y−y_0, x₀ − x₁ y₀ − y₁

x − ^{a √}b² − y² _{y − y} √^b√⁰=⁰,

^a b² − y² − ^a b² − y^{2 y}0 ^{− y}1 b⁰b¹

98

(^bx−^√b² −y²)(^√b² −y² +^√b² −y²) _{y−y a}001₌0_,

y ₁² − y ₀² y ₀ − y ₁ (^bx−√b² −y₀²)(√b² −y₀² +√b² −y₁²)=(y₀ −y)(y₀ +y₁).

a
Если точка M₁ стремиться к точке M₀ по эллипсу, то y₁ стремиться к y₀. Тогда последнее равенство

можно записать в виде

Разделим это равенство на b² :
_√ ab b²

Учитывая, что x₀ = ^a b² − y², получаем:

^x ⋅ ^a √ b ² − y ₀² + ^{y y 0} = 1 , a²b b²

^xx0 ₊ ^yy0 _{= 1.} a² b²

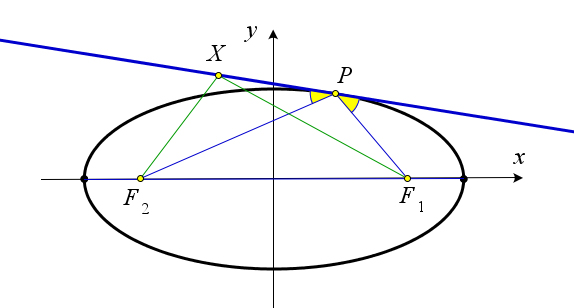
липса, отразившись от какой-либо точки эллипса, проходит через другой его фокус.

Рис. 168. Теорема 10.2.7.

Доказательство.

Пусть к данному эллипсу в точке P проведена касательная (рис. 168). Пусть X – это произвольная точка этой касательной, отличная от точки P. Очевидно, что точка X лежит вне эллипса, следова- тельно,F₁X+XF₂ >F₁P+PF₂.ТакимобразомминимумсуммыF₁X+XF₂ достигается,еслиточка X совпадает с точкой P. Тогда по теореме 11.3.6 лучи PF₁ и PF₂ образуют одинаковые углы с каса- тельной, что соответствует правилу отражения лучей света.

10.2.4 Гипербола
Определение 10.3. Гипербола – это геометрическое место точек, модуль разности расстояний от

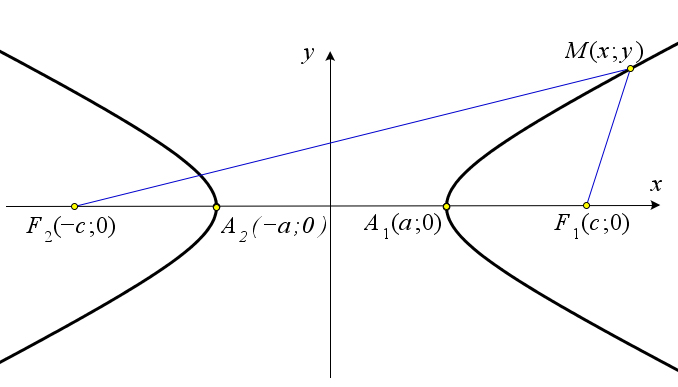
которых до двух данных точек F₁ и F₂ постоянен и при этом меньше, чем ∣F₁F₂∣.

Теорема 10.2.8. Каноническое уравнение гиперболы имеет вид ^x2 − ^y2 = 1, число a называется ве- a² b²

щественной полуосью гиперболы, b – мнимой полуосью.

Рис. 169. Теорема 10.2.8.

(^bx−√b² −y₀²)⋅2√b² −y₀² =(y₀ −y)⋅2y₀, ^a_√

^bx b²−y²−b²+y²=y²−yy,

000^{0 b} x √ b ² − y ₀² + y y ₀ = b ² .

a
a

√
¹ x b ² − y ₀² + ^{y y 0} = 1 .

b0

Случай, когда абсциссы точек M и M отрицательны рассматривается аналогично, с той лишь раз-

01
ницей, что теперь координаты этих точек будут иметь вид M₀(−^a b² −y²;y₀),M₁(−^a b² −y²;y₁).

√√

b⁰b¹ Теорема 10.2.7 (Оптические свойство эллипса). Любой луч света, вышедший из одного фокуса эл-

99

Доказательство.

Пусть M(x,y) – это произвольная точка, принадлежащая данной гиперболе, а точки F₁(c;0) и F₂(−c;0) – это её фокусы (рис. 168). Тогда по определению гиперболы ∣MF₁ −MF₂∣ постоянен. Пусть этот модуль равен 2a, то есть ∣M F₁ − M F₂ ∣ = 2a. Распишем это равенство с помощью формулы рассто- яния между двумя точками:

∣^√(x−c)² +y² −^√(x+c)² +y²∣=2a
Возведём это равенство в квадрат, раскроем скобки и приведём подобные слагаемые:

2x² +2c² +2y² −2^√(x−c)² +y^2√(x+c)² +y² =4a². ^√(x−c)² +y^2√(x+c)² +y² =x² +y² +c² −2a².

или
При условии, что x² + y² + c² − 2a² ⩾ 0, данное уравнение можно возвести в квадрат:

или

((x−c)² +y²)((x+c)² +y²)=4a⁴ −4a²(x² +y² +c²)+(x² +y² +c²)²
(x² +c² +y² −2xc)(x² +c² +y² +2xc)=4a⁴ −4a²x² −4a²y² −4a²c² +(x² +y² +c²)².

В левой части раскроем скобки, используя формулу разности квадратов:

(x² +y² +c²)² −4x²c² =4a⁴ −2a²x² −2a²y² −2a²c² +(x² +y² +c²)².
Сократив подобные слагаемые, перенеся все слагаемые в одну часть, и сократив на 4, получим:

Перегруппируем слагаемые:

a⁴ −a²x² −a²y² −a²c² +x²c² =0.

(a⁴ −a²c²)+(x²c² −x²a²)−a²y² =0, x²(a² − c²) + a²y² = a²(a² − c²)

. Так как a < c, то можно разделить последнее равенство на a²(a² − c²): ^x2+ ^y2 =1.

a² a² − c^2
x2 − ^y2 = 1. (1)

Обозначив b² = c² − a², получим
Теперь докажем, что любая пара чисел (x,y), удовлетворяющая последнему равенству, удовлетво-

a² b²
ряет условию (x² + y² + c²) − 2a² ⩾ 0. Преобразуем левую часть:

x² +y² +c² −2a² =x² +y² −a² +(c² −a²)=x² +y² −a² +b². Изравенства1следует,чтоx² =a²(1+^y2)⩾a²,таккак1+^y2 ⩽1.Следовательно,x² ⩾a²,азначит,

или Следовательно,

b² b² x² +y² −a² +b² ⩾y² +b² ⩾0

x² + y² − a² + b² ⩾ 0. x² +y² +c² −2a² ⩾0.

Замечание (свойства канонической гиперболы).

1. Вершины гиперболы имеют координаты A_1,2(±a;0).

2. Каноническая гипербола имеет две асимптоты с уравнениями y = ± ^b x. a

3. Фокусы канонической гиперболы имеют координаты F₁ (c; 0) и F₂ (−c; 0), при этом b² = c² − a² и c > a.

100

4. Эксцентриситетом гиперболы называется число e = ^c . a

Теорема 10.2.9 (касательная к гиперболе). Пусть точка M(x₀;y₀) – произвольная точка гиперболы ^x2 − ^y2 = 1. Тогда уравнение касательной к гиперболе, проведенной в этой точке имеет вид ^xx0 − ^yy0 = 1.

a² b²

a² b²

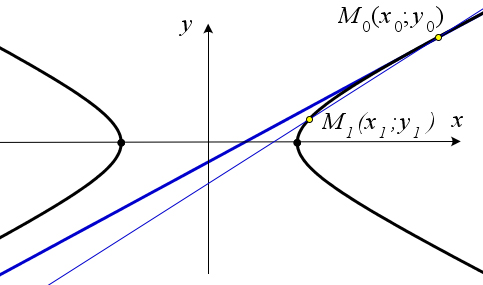
Доказательство.

Рис. 170. Теорема 10.2.9.

По определению касательной к кривой в данной токе M называется предельное положение секущей

M₀M₁ при условии, что точка M₁ стремится к точке M₀ по данной кривой. Рассмотрим уравнение

секущей к эллипсу, проходящей через точку M₀(x₀;y₀) и не совпадающую с ней точку M₁(x₁;y₁).

Поскольку точка M₁ стремится к точке M₀, знаки их абсцисс совпадают. Рассмотрим случай, когда

абсциссы точек M и M положительны (рис. 170). Так как обе точки лежат на гиперболе ^x2 + ^y2 = 1, ⁰¹ _√√a²b²

то их координаты можно записать в виде M₀(^a b² +y²;y₀),M₁(^a b² +y²;y₁). Запишем уравнение

прямой M₀M₁:

b⁰b¹ x−x_{0 =}y−y_0,

x − ^{a √}b² + y² _{y − y} √^b√⁰=⁰,

x₀ − x₁ y₀ − y₁

b² + y² − ^a b² + y^{2 y}0 ^{− y}1 (^bx−^√b² +y²)(^√b² +y² +^√b² +y²) _y−y

a b⁰b¹

_a001₌0_, y ₀² − y ₁² y ₀ − y ₁

(^bx−√b² +y₀²)(√b² −y₀² +√b² −y₁²)=(y−y₀)(y₀ +y₁). a

Если точка M₁ стремиться к точке M₀ по эллипсу, то y₁ стремиться к y₀. Тогда последнее равенство

можно записать в виде

Разделим это равенство на b²: Учитывая, что x₀ = ^{a √}b² + y², получаем:

^x _⋅ ^{a √} _b ² _{+ y 0}² ₋ ^{y y 0} _{= 1 ,} a²b b²

^xx0 ₋ ^yy0 _{= 1.} a² b²

(^bx−√b² +y₀²)⋅2√b² +y₀² =(y−y₀)⋅2y₀, ^a_√

^bx b²+y²−b²−y²=yy −y²,

00⁰0 ^b x √ b ² + y ₀² − y y ₀ = b ² .

a
a

√
¹ x b ² + y ₀² − ^{y y 0} = 1 .

ab b²

b0

и M отрицательны рассматривается аналогично, с той лишь раз-

Случай, когда абсциссы точек M
ницей, что теперь координаты этих точек будут иметь вид M₀(−^a b² +y²;y₀),M₁(−^a b² +y²;y₁).

01

√√

Лемма 10.2.10. Максимум модуля разности расстояний от точки данной прямой l до точек F₁ и F₂, лежащих по разные стороны от данной прямой достигается в такой точке P, для которой лучи PF₁ и PF₂ образуют равные углы с прямой l.

101

b⁰b¹

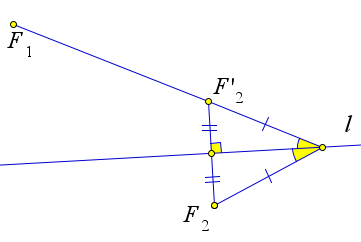
Доказательство.

Рис. 171. Лемма 10.2.10.

Обозначим через F₂^′ точку, симметричную F₂ относительно прямой l (рис. 171). Очевидно, что F₂X = F₂^′X для любой точки X на прямой l. Нам достаточно найти такую точку P, что разность расстояний от P до F₁ и F₂^′ будет как можно больше. Из неравенства треугольника следует, что ∣F₁P −F₂^′P∣ < F₁F₂^′. И достигается этот максимум тогда и только тогда, когда точки F₁,F₂,P лежат на одной прямой. Поскольку точки F₂ и F₂^′ симметричны, углы, которые образуют прямые F₁P и F₂P с прямой l, равны.

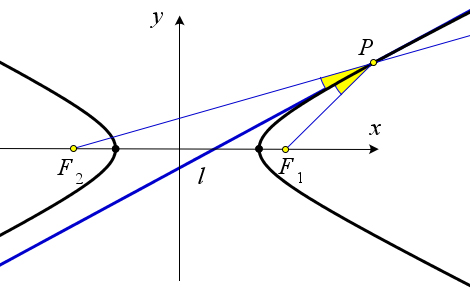
Теорема 10.2.11 (оптическое свойство гиперболы). Луч света, вышедший из фокуса F₂, отразившись от какой-либо точки M гиперболы, распространяется далее вдоль луча F₁M, то есть так, как если бы луч света исходил из фокуса F₁ и распространялся бы без помех.

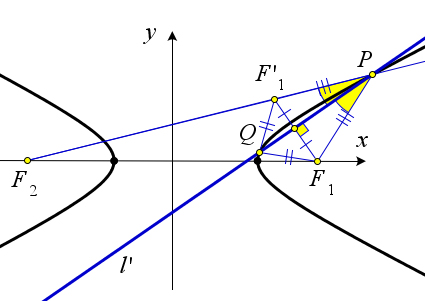
Доказательство.

a)

b)

Рис. 172. Теорема 10.2.11.

Переформулируем утверждение: если прямая l касается гиперболы в точке P, то l является бис- сектрисой угла F₁PF₂, где F₁ и F₂ – фокусы гиперболы (рис. 172 a).

Предположим, что биссектриса l^′ угла F₁PF₂ пересекает гиперболу ещё в какой-нибудь точке Q (лежащей на той же дуге, что и P) (рис. 172 b). Для удобства будем считать, что точка P лежит на дуге, которая ближе к фокусу F₁. Обозначим через F₁^′ точку, симметричную F₁ относительно l^′. ТогдаF₁Q=QF₁^′,F₁P=PF₁^′;крометого,точкиF₂,F₁^′ иPлежатнаоднойпрямой.Итак,F₂P−PF₁= F₂Q−F₁Q.ВсилувышеуказанныхравенствполучаемF₂F₁^′ =F₂P−PF₁^′ =F₂Q−QF₁^′.Нопонеравенству треугольника F₂F₁^′ > F₂Q−QF₁^′. Таким образом получено противоречие, что и доказывает утверждение теоремы.