5.4 Тригонометрические функции в прямоугольном треугольнике

Определение 5.5 (Определение в прямоугольном треугольнике). Синусом острого угла прямоуголь- ного треугольника называется отношения противолежащего катета к гипотенузе.

Определение 5.6 (Определение в прямоугольном треугольнике). Косинусом острого угла прямо- угольного треугольника называется отношение прилежащего катета к гипотенузе.

Определение 5.7. Тангенсом острого угла прямоугольного треугольника называется отношение про- тиволежащего катета к прилежащему катету.

Определение 5.8. Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.

Теорема 5.4.1 (Основные формулы тригонометрии).

1. sin²α+cos²α=1.

2.tg²α+1= ¹ . _cos² _α

3. sin(90^○ −α)=cosα; cos(90^○ −α)=sinα; tg(90^○ −α)=ctgα, при α<90^○.

49

Доказательство.

a)

b)

Рис. 84. Теорема 5.4.1.

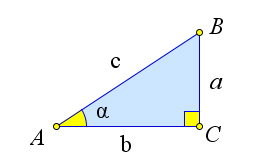
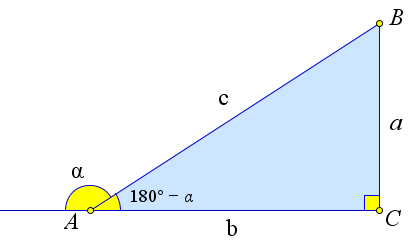
Рассмотрим прямоугольный треугольник ABC, в котором _∠C = 90^○, _∠A = α, BC = a, AC = b, AB = c (рис.84a).Тогдаsin²α+cos²α=^a2 +^b2 =^a2^+b2 =^c2 =1.Еслиуголαтупой,тоsinα=sin(180^○−α)и

c² c² c² c²
cosα=−cos(180^○ −α)(рис.84b).Атаккакугол180^○−α–острый,то1=sin²(180^○ −α)+cos²(180^○ −α)=

sin² α + (− cos α)² = sin² α + cos² α. Докажем второй пункт теоремы. _tg2α+1= sin²α ₊₁₌ sin²α+cos²α ₌ 1 _.

cos² α cos² α cos² α
Рассмотрим прямоугольный треугольник ABC, в котором _∠C = 90^○, _∠A = α, BC = a, AC = b, AB = c

Докажем третий пункт теоремы.
(рис.84a).Тогдаsin(90^○−α)=sinB=^b =cosα,cos(90^○−α)=cosB=^a =sinα,tg(90^○−α)=tgB=^b =

ctg α.
Теорема 5.4.2 (Значения тригонометрических функций стандартных углов).

○1○3○1 1. sin30 = ,cos30 = ,tg30 = ^√ .

22

√√

√

cca

22₃

√ 3. sin45^○ = ²,cos45^○ = ²,tg45^○ = 1.

√
2. sin60^○ = ³,cos60^○ = ¹,tg60^○ = 3.

22

Доказательство.

a)

Рис. 85. Теорема 5.4.2.

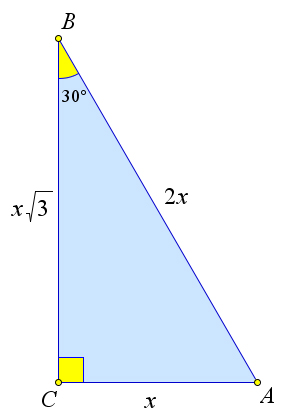
Рассмотрим прямоугольный треугольник ABC, в котором _∠B = 30^○. Тогда катет AC в два раза меньше гипотенузы AB: AC = x, AB = 2x. По теореме Пифагора BC = ^√4x² − x² = x^√3. Тогда sin B =

sin30^○=^x =¹, 2x 2

○x1 tgB=tg30 = ^√ =^√ ,

cosA=cos60^○=^{x 3}= ³, 2x 2

b)

cosB=cos30^○=^{x 3}= ³, 2x 2

√√

x33 √√

50

sinA=sin60^○=^x =¹, 2x 2

√
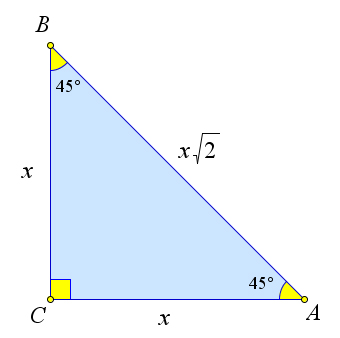
Рассмотримxпрямоугольный треугольник ABC, в котором _∠C = 90^○,_∠A = _∠B = 45^○. Обозначим

√ tgA=tg60^○=^{x 3}= 3.

22 ^○x BC=AC=x,тогдапотеоремеПифагораAB=^√x +x =x^√2.ТогдаsinA=sin45 = ^√ =cosA=

cos 45^○ .
6 Окружность

x2

Определение 6.1. Окружность – это геометрическое место точек, равноудаленных от данной точки. 6.1 Касательные и хорды

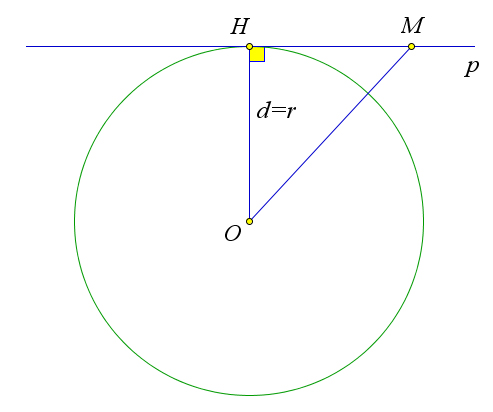
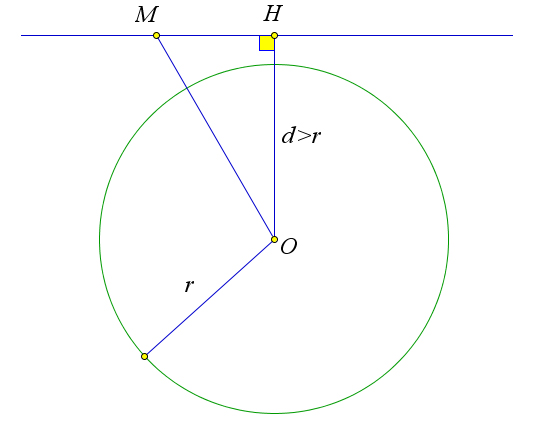
Теорема 6.1.1. Если d – это расстояние от точки O до прямой l, а ω – окружность с центром в точке O и радиусом R, тогда

1. если d > R, то прямая не пересекает окружность;
2. если d = R, то прямая является касательной к окружности; 3. если d < R, то прямая пересекает окружность в двух точках.

a) b)
Рис. 86. Теорема 6.1.1.

Доказательство.

c)

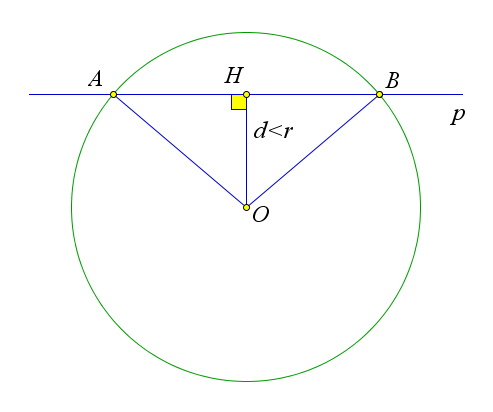
Пусть d < r (рис. 86 a). На прямой p от точки H отложим два отрезка HA и HB, длины которых равны ^√r² − d². По теореме Пифагора OA = OB = ^√OH² + HA² = ^√d² + (r² − d²) = r. Следовательно, точки A и B лежат на окружности и, значит, являются общими точками прямой p и данной окружно- сти.

Докажем, что прямая p и данная окружность не имеют других общих точек. Предположим, что они имеют ещё одну общую точку C. Тогда медиана OD равнобедренного треугольника OAC, проведенная к основанию AC, является высотой этого треугольника, поэтому OD ⊥ p. Отрезки OD и OH не совпа- дают, так как середина D отрезка AC не совпадает с точкой H – серединой отрезка AB. Получается, что из точки O проведены два перпендикуляра: отрезки OH и OD – к прямой p, что невозможно.

Пусть d = r (рис. 86 b). В этом случае OH = r, то есть точка H лежит на окружности и, значит, является общей точкой прямой и окружности. Прямая p и окружность не имеют других общих точек, так как для любой точки M прямой p, отличной от точки H, OM > OH = r (наклонная OM больше перпендикуляра OH), и, следовательно, точка M не лежит на окружности.

Пусть d > r. В этом случае OH > r, поэтому для любой точки M прямой p OM ⩾ OH > r. Следова- тельно, точка M не лежит на окружности.

Определение 6.2.

1. Прямая, имеющая с окружностью только одну общую точку, называется касательной к этой окружности.

2. Прямая, имеющая с окружностью две общие точки, называется секущей к данной окружностью.

Определение 6.3. Касательная к кривой – это предельное положение секущей. Теорема 6.1.2 (о характерном свойстве касательной).

51

1. (Свойство касательной): касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

2. (Признак касательной): если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведенному в эту точку, то она является касательной. 
Рис. 87. Теорема 6.1.2.

Доказательство.

Докажем первый пункт теоремы.
Пусть p – касательная к окружности с центром O, A – точка касания (рис. 87). докажем, что p ⊥ OA. Предположим, что это не так. Тогда радиус OA является наклонной к прямой p. Так как перпен-

дикуляр, проведенный из точки O к прямой p, меньше наклонной OA, то расстояние от от точки O до прямой p меньше радиуса. Следовательно, прямая p и окружность имеют две общие точки. Но это противоречит условию, так как p – это касательная. Таким образом p ⊥ OA.

Докажем второй пункт теоремы.

Из условия следует, что данный радиус является перпендикуляром, проведенным из центра окруж- ности к данной прямой. Поэтому расстояние от центра окружности до прямой равно радиусу, и, сле- довательно, прямая и окружность имеют только одну общую точку. Но это и означает, что данная прямая является касательной к окружности.

Теорема 6.1.3.

1. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

2. Если прямые, проходящие через точку M, касаются окружности в точках A и B, то MA =

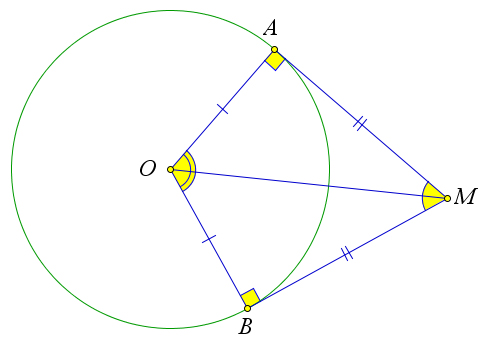
MB.

Доказательство.

Рис. 88. Теорема 6.1.3.

Рассмотрим окружность с центром в точке O, вписанную в угол M. Пусть данная окружность касается сторон угла в точках A и B (рис. 88). Докажем, что _∠AMO = _∠BMO.

Действительно, треугольники AMO и BMO равны, по катету и гипотенузе (OA = OB, OM – общая). Тогда _∠AMO = _∠BMO и MA = MB.

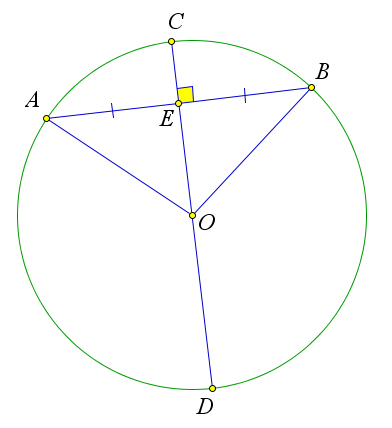
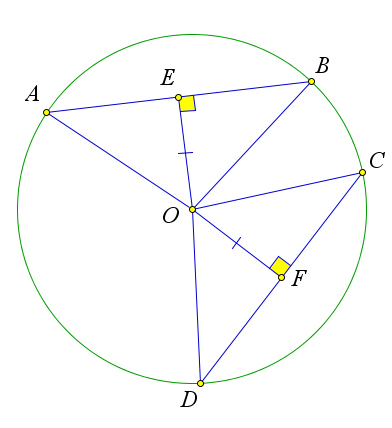
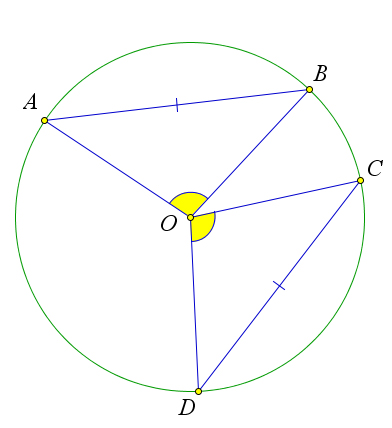
Теорема 6.1.4 (Свойства хорд окружности).

• 1^○  Диаметр перпендикулярен хорде, тогда и только тогда, когда он проходит через ее середину.

• 2^○  Хорды одной окружности равны тогда и только тогда, когда они равноудалены от ее центра.

• 3^○  Хорды одной окружности равны тогда и только тогда, когда они стягивают равные централь- ные углы.

52

a) b) c) Рис. 89. Теорема 6.1.4.

Доказательство.

Докажем первый пункт теоремы.
Рассмотрим окружность с центром O, в которой хорда AB пересекает диаметр CD в точке E. Если E – это середина AB, то OE – это медиана равнобедренного треугольника AOB, а, следова-

тельно, и OE – высота. Обратно, если OE - высота, то и медиана.
Докажем второй пункт теоремы.
Рассмотрим окружность с центром O, в которой проведены хорды AB и CD. Пусть расстояния

OE и CD до этих хорд равны. Тогда треугольники OAE,OEB,OFD и OFC равны по катеты и гипотенузе (OA = OB = OD = OC, так как это радиусы). Тогда AE = EB = DF = FC, и, следовательно, AB = 2AE = 2DF = CD.

Докажем третий пункт теоремы.

Рассмотрим окружность с центром O, в которой проведены хорды AB и CD. Если _∠AOB = _∠COD, то _△AOB = _△COD по первому признаку равенства (CO = OB = OD = OA, так как это радиусы), сле- довательно, AB = CD. Обратно, если AB = CD, то _△AOB = _△COD по третьему признаку равенства, следовательно, _∠AOB = _∠COD.

6.2 Две окружности

Теорема 6.2.1.

1. Точка касания двух окружностей лежит на прямой, соединяющей их центры.

2. Центры двух пересекающихся окружностей лежат на серединном перпендикуляре к их общей хорде.

Теорема 6.2.2 (о взаимном расположении двух окружностей).
1. Если R + r < d, то окружности не пересекаются, и одна лежит вне другой.
2. Если R + r = d, то окружности касаются внешним образом.
3. Если R − r < d < R + r, то окружности пересекаются.
4. Если R − r = d, то окружности касаются внешним образом.
5. Если R − r > d, то окружности не пересекаются, и одна окружность лежит внутри другой.

6.3 Углы в окружности

Определение 6.4. Угол с вершиной в центре окружности называется ее центральным углом. Определение 6.5. Градусной мерой дуги окружности называется величина центрального угла, ко-

торый соответствует этой дуге.

Определение 6.6. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

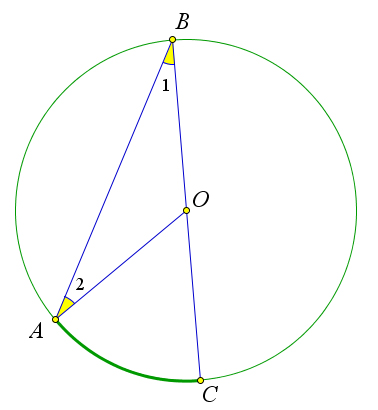
Теорема 6.3.1 (о вписанном угле). Вписанный угол измеряется половиной дуги, на которую он опи- рается.

53

a)

b)

Доказательство.

c)
Рис. 90. Теорема 6.3.1.

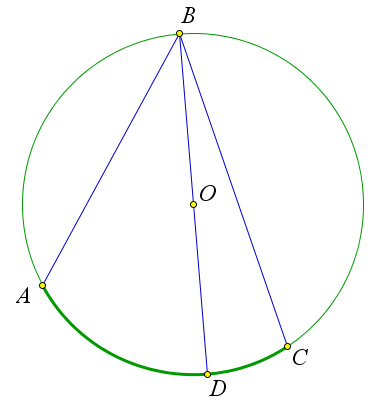
Пусть _∠ABC – вписанный угол окружности с центром O, опирающийся на дугу AC. Докажем, что _∠ABC = ¹ _􏰂AC. Рассмотрим три возможных случая расположения луча BO относительно угла ABC.

2

Первый случай. Пусть луч BO совпадает с одной из сторон угла ABC, например со стороной

BC (рис. 90 a). В этом случае дуга AC меньше полуокружности, поэтому _∠AOC = _􏰂AC. Так как

угол AOC – внешний угол равнобедренного треугольника ABO, и _∠1 = _∠2, как углы при основании

равнобедренного треугольника, то _∠AOC = _∠1 + _∠2 = 2_∠1. Отсюда следует, что 2_∠1 = _􏰂AC или

_∠ABC = _∠1 = ¹ _􏰂AC. 2

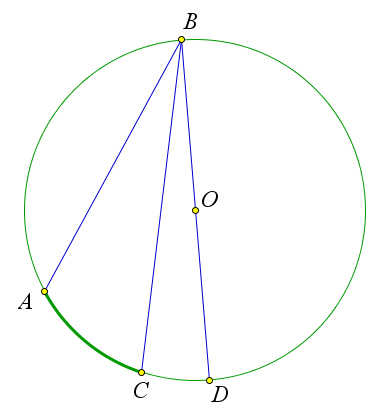
Второй случай. Пусть луч BO делит угол ABC на два угла. В этом случае луч BO пересекает дугу

AC в некоторой точке D (рис. 90 b). Точка D разделяет дугу AC на две дуги: _􏰂AD и _􏰂DC. По первому

случаю _∠ABD = ¹ _􏰂AD и _∠DBC = ¹ _􏰂DC. Складывая эти равенства, получим: _∠ABD + _∠DBC = 22

Третий случай. Пусть луч BO пересекает окружность в точке D, при этом луч BC разбивает угол

ABD на два угла (рис. 90 c). Точка C разделяет дугу AD на две дуги: _􏰂AC и _􏰂CD. По первому

случаю _∠ABD = ¹ _􏰂AD и _∠DBC = ¹ _􏰂DC. Вычитая эти равенства, получим: _∠ABD − _∠CBD = 22

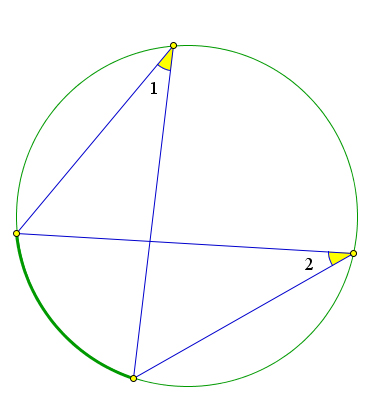
Следствие 6.3.1.1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

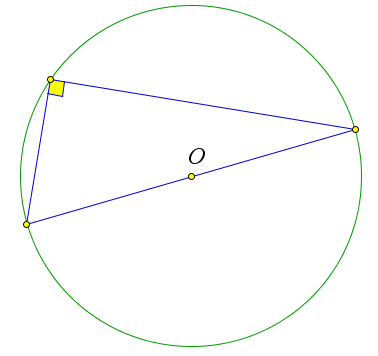
Рис. 91. Следствие 6.3.1.1.
Следствие 6.3.1.2. Вписанный угол, опирающийся на диаметр – прямой.

¹ _􏰂AD + ¹ _􏰂DC = ¹ _􏰂AC. 222

¹ _􏰂AD − ¹ _􏰂CD = ¹ _􏰂AC. 222

54

Теорема 6.3.2.

Рис. 92. Следствие 6.3.1.2.

1. Угол между пересекающимися хордами окружности равен полусумме двух противоположных дуг, высекаемых этими хордами.

2. Угол между двумя пересекающимися секущими данной окружности равен полуразности дуг, высекаемых этими секущими.

3. Угол между двумя пересекающимися касательными к окружности равен 180^○ − α, где α – гра- дусная мера меньшей из дуг, образованных точками касания.

4. Угол между касательной и хордой, проведенной из точки касания, равен половине дуги, заклю- ченной между ними.

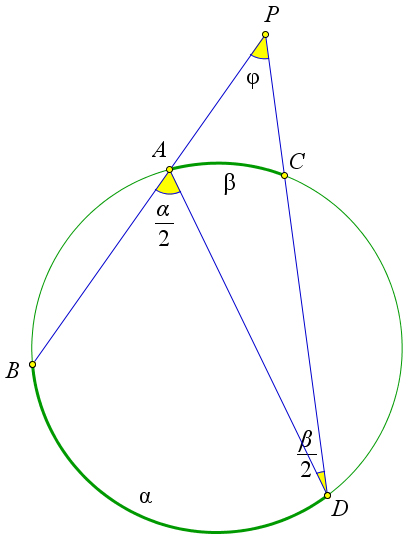
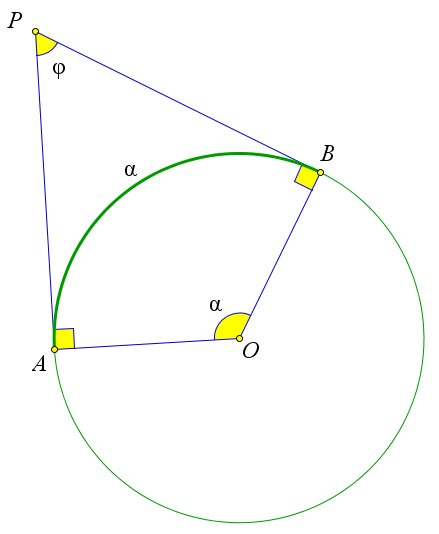
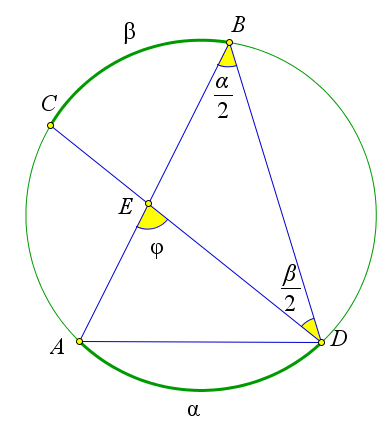
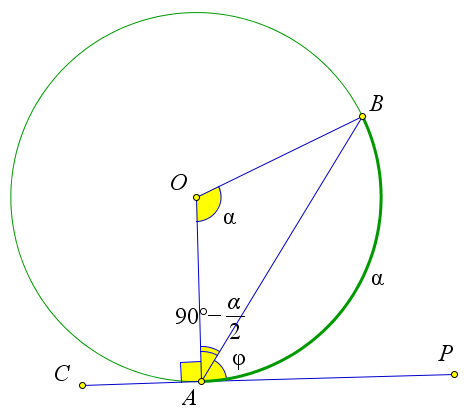
a)

c)

b)

d)
Рис. 93. Теорема 6.3.2.

Доказательство.

Докажем первый пункт теоремы.

Пусть хорды AB и CD окружности ω пересекаются в точке E. Обозначим _∠φ = _∠AED,α = _􏰂AD, β = _􏰂BC (рис. 93 a). Докажем, что _∠φ = ^α+β .

2

Углы ABD и CDB – вписанные, поэтому _∠ABD = ^α , _∠CDB = ^β . Кроме того _∠φ – внешний угол

треугольника EBD, поэтому _∠φ = ^α + ^β = ^α+β . 222

Докажем второй пункт теоремы.

Пусть секущие PB и PD пересекают окружность ω в точках A и C соответственно (рис. 93 b).

Обозначим α = _􏰂BD,β = _􏰂AC,_∠φ = _∠P. Докажем, что тогда φ = ^α−β . 2

22

55

Углы BAD и ADC – вписанные, поэтому _∠BAD = ^α , _∠ADC = ^β . Кроме того _∠BAD – внешний 22

угол треугольника P AD? следовательно, ^α = _∠φ + ^β , откуда _∠φ = ^α−β .

Докажем третий пункт теоремы.

Пусть из точки P к окружности с центром O проведены две касательные PA и PB (A и B – точки касания) (рис. 93 c). Обозначим _􏰂AB = α. Угол AOB – центральный, поэтому _∠AOB = α. Кроме того _∠PAO = _∠PBO = 90^○. Поскольку сумма углов четырехугольника PAOB равна 360^○, то _∠P =_∠φ=360^○ −90^○ −90^○ −α=180^○ −α.

Докажем четвертый пункт теоремы.

222

Пусть прямая P C касается окружности с центром O в точке A. Кроме того пусть проведена хорда AB. Обозначим α = _􏰂AB (рис. 93 d). Докажем, что тогда _∠P AB = ^α .

2

Угол AOB центральный, поэтому он равен α. Кроме того, треугольник AOB равнобедренный, следовательно, _∠OAB = ¹⁸⁰X^−α = 90^○ − ^α . Угол OAP равен 90^○, так как это угол между касательной и

радиусом. Тогда _∠φ = _∠P AB = 90^○ − (90^○ − ^α ) = ^α . 22

6.4 Пропорциональные отрезки в круге

Теорема 6.4.1 (о произведении отрезков хорд). Если две хорды окружности пересекаются, то про- изведение отрезков одной хорды, равно произведению отрезков другой хорды.

Рис. 94. Теорема 6.4.1.

Доказательство.

Пусть в окружности хорды AB и CD пересекаются в точке E (рис. 94). Докажем, что AE ⋅ EB = CE ⋅ ED.

22

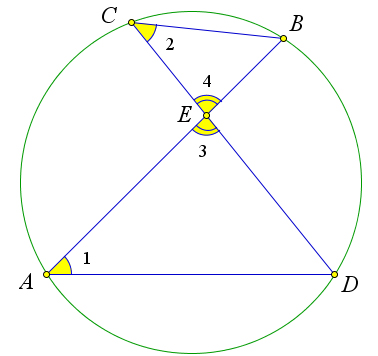
Рассмотрим треугольники ADE и CBE. В этих треугольниках _∠1 = _∠2 = ¹_􏰂BD, так как они

вписанные. Кроме того _∠3 = _∠4, как вертикальные. Следовательно, _△ADE ∼2_△CBE по первому

признаку подобия. Отсюда ^AE = ^DE , или AE ⋅ EB = CE ⋅ ED. CE BE

Теорема 6.4.2 (о квадрате касательной). Если через точку M проведена касательная MK (K – точка касания) и секущая, пересекающая окружность в точках A и B, то MK² = MA ⋅ MB.

Рис. 95. Теорема 6.4.2.

Доказательство.

Пусть из точки M к окружности проведены касательная MK и секущая MB, пересекающая окруж- ность в точке A (рис. 95). Докажем, что MK² = MA ⋅ MB.

Обозначим α = _􏰂AK. Тогда _∠B = ^α. Кроме того _∠MKA = ^α, как угол между касательной и 22

^KM =^BM,илиKM²=AM⋅BM. AM KM

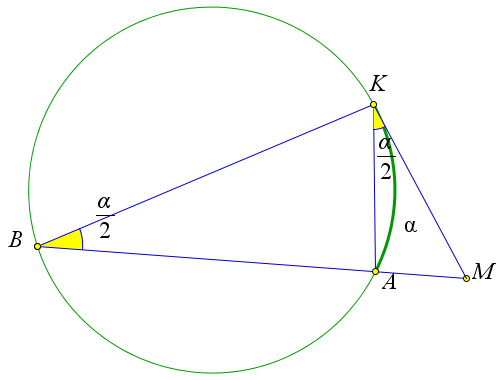
хордой. Тогда _△MKA ∼ _△MKB по первому признаку подобия (_∠B = _∠MKA, _∠M – общий). Тогда

56

Теорема 6.4.3 (о произведении отрезков секущих). Если через точку M проведены две секущие, одна из которых пересекает окружность в точках A и B, а другая – в точках C и D, то MA ⋅ MB = MC ⋅ MD.

Рис. 96. Теорема 6.4.3.

Доказательство.

Пусть через точку M проведены две секущие, одна из которых пересекает окружность в точках A и B, а другая – в точках C и D (рис. 96). Докажем что MA ⋅ MB = MC ⋅ MD.

Проведем из точки M к данной окружности касательную M K . По теореме 6.4.2 M K ² = M A ⋅ M B иMK² =MC⋅MD,откудаMA⋅MB=MC⋅MD.

Определение 6.7. Пусть через точку M проведена прямая, пересекающая данную окружность в точках A и B. Степенью точки M относительно данной окружности называется произведение MA⋅MB.

Теорема 6.4.4. Степень точки относительно данной окружность не зависит от выбора прямой. Доказательство.

Эта теорема является прямым следствием теорем 6.4.1, 6.4.2, 6.4.3.

6.5 Четыре замечательные точки треугольника

Определение 6.8. Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в таком случае называется описанным.

Определение 6.9. Окружность называется описанной около многоугольника, если она проходит че- рез все его вершины. Многоугольник в таком случае называется вписанным в данную окружность.

Определение 6.10. Точка пересечения медиан треугольника называется центроидом или центром масс.

Замечание. Медианы треугольника пересекаются в одной точке по теореме 4.2.1.
Теорема 6.5.1 (о биссектрисе, как ГМТ). Биссектриса неразвернутого угла – это геометрическое

место точек, равноудаленных от его сторон.

Доказательство.

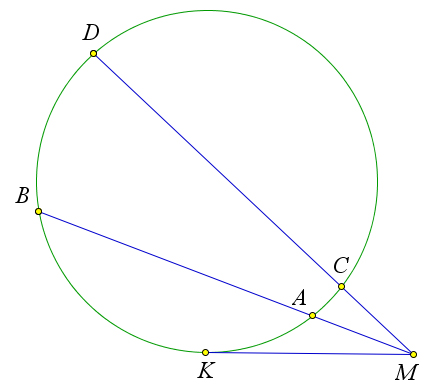
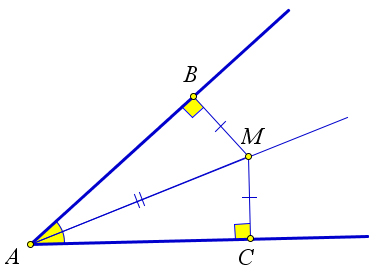
Рассмотрим угол _∠A.

Рис. 97. Теорема 6.5.1.

Докажем, что любая точка, принадлежащая биссектрисе равноудалена от сторон этого угла. Возь- мём произвольную точку M на биссектрисе угла A и опустим из неё перпендикуляры MB и MC на

57

стороны данного угла. Треугольники AMB и AMC равны по гипотенузе и острому углу, поэтому MB = MC, и следовательно, точка M равноудалена от сторон угла.

Обратно: докажем, что если точка равноудалена от сторон угла, то она лежит на биссектрисе. Возьмём произвольную точку M, из которой опущены перпендикуляры MB и MC на стороны угла и при этом MB = MC. Докажем, что точка M принадлежит биссектрисе. Треугольники AMB и AMC равны по гипотенузе и катету, следовательно, _∠BAM = _∠CAM, то есть AM – биссектриса угла _∠A.

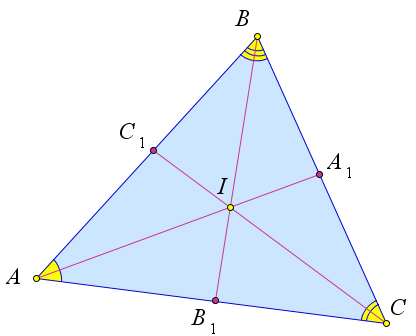
Теорема 6.5.2. Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

Первый способ.

Рис. 98. Теорема ??.

Рассмотрим треугольник ABC в котором проведены биссектрисы AA₁, BB₁ и CC₁ (рис. 98). По теореме 3.3.2 ^AC1 = ^AC , ^BA1 = ^AB , ^CB1 = ^BC . Перемножая эти равенства, получим: ^AC1 ⋅ ^BA1 ⋅ ^CB1 =

C₁B BC A₁C AC
^AC ⋅ ^AB ⋅ ^BC = 1, а это по теореме Чевы означает, что биссектрисы AA₁,BB₁ и CC₁ пересекаются в

BC AC BA

B₁A BA C₁B

A₁C B₁A

одной точке.
Второй способ.
Рассмотрим треугольник ABC в котором проведены биссектрисы AA₁, BB₁ и CC₁ (рис. 98). До-

кажем, что все биссектрисы пересекаются в одной точке. Пусть биссектрисы AA₁ и BB₁ пересекаются в точке I. Тогда по теореме (рис. 97) ρ(I;AB) = ρ(I;AC), так как I ∈ AA₁, и ρ(I;BA) = ρ(I;BC), так как I ∈ BB₁. Тогда ρ(I;CA) = ρ(I;CB), что означает, что I ∈ CC₁, то есть все три биссектрисы пересекаются в одной точке.

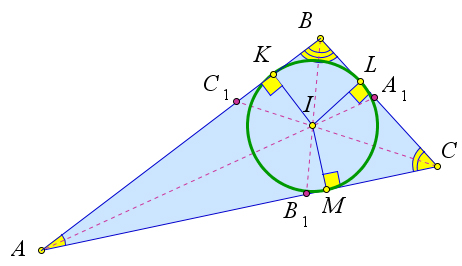
Следствие 6.5.2.1. В любой треугольник можно вписать окружность, центром которой будет являться точка пересечения его биссектрис. Такая окружность единственна.

Рис. 99. Теорема 6.5.2.1.

Доказательство.

Рассмотрим произвольный треугольник ABC и обозначим буквой I точку пересечения его биссек- трис. Проведем из этой точки перпендикуляры IK,IL и IM к сторонам AB,BC и CA соответственно (рис. 99). Так как точка I равноудалена от сторон треугольника, то IK = IL = IM. Поэтому окруж- ность с центром I радиуса IK проходит через точки K,L и M. Стороны треугольника ABC касаются этой окружности в точках K,L,M так как они перпендикулярны к радиусам IK,IL и IM. Значит окружность с центром I радиуса IK является вписанной в треугольник ABC.

Докажем, что такая окружность единственна. В самом деле, допустим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудалён от сторон треугольника и, значит совпадает с точкой I пересечения биссектрис треугольника, а радиус равен расстоянию от точки I до сторон треугольника. Следовательно, эти окружности совпадают.

Следствие 6.5.2.2. Если все биссектрисы выпуклого многоугольника пересекаются в одной точке, то в него можно вписать окружность, центром которой будет точка пересечения биссектрис.

58

Доказательство.

Если все биссектрисы пересекаются в одной точке, то эта точка будет равноудалена от всех её сторон, то есть перпендикуляры к сторонам многоугольника будут равны, а окружность с центром в этой точке и с радиусом, равным расстоянию от точки пересечения биссектрис до стороны, будет касаться всех сторон.

Теорема 6.5.3 (о серединном перпендикуляре, как ГМТ). Серединный перпендикуляр к отрезку – это геометрическое место точек, равноудаленных от концов отрезка.

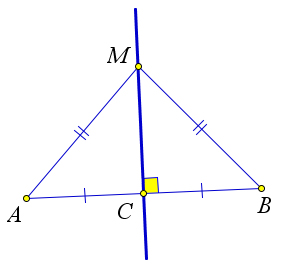
Рис. 100. Теорема 6.5.3.

Доказательство.

Рассмотрим отрезок AB. Середину отрезка обозначим C. Докажем, что любая точка, принадле- жащая серединному перпендикуляру, равноудалена от сторон. Действительно, возьмём произвольную точку M на серединном перпендикуляре. Если M = C, то очевидно, что MA = MB. Если M ≠ C, то треугольники AMC и BMC равны по двум катетам, следовательно AM = MB.

Обратно, докажем, что любая точка равноудалённая от сторон, принадлежит серединному пер- пендикуляру. Возьмём произвольную точку M, для которой MA = MB. Если M = C, то очевидно, M принадлежит серединному перпендикуляру. Если MC, то треугольник AMB – равнобедренный, и, следовательно, медиана MC является высотой, то есть MC – серединный перпендикуляр.

Следствие 6.5.3.1. Все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

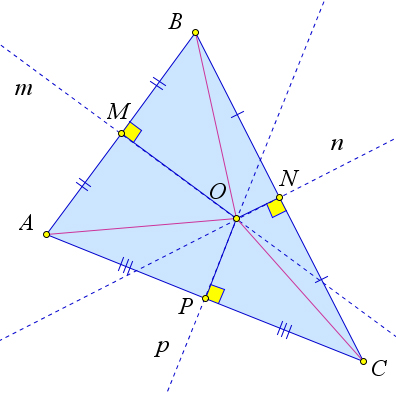
Рис. 101. Теорема 6.5.3.1.

Доказательство.

Рассмотрим произвольный треугольник ABC, в котором точки M,N и P являются серединами сторон AB,BC и CA (рис. 101). Обозначим серединные перпендикуляры к сторонам AB,BC,AC как m,n,p. Докажем, что эти серединные перпендикуляры пересекаются в одной точке.

Если предположить, что m ∥ n, то получится, что n ⊥ BA, так как m ⊥ BA. Но тогда получится, что через точку B проходят две различные прямые BA и BC, перпендикулярные прямой n, что невозмож- но, следовательно, прямые m и n пересекаются. Пусть они пересекаются в точке O. Тогда по теореме 6.5.3 OA = OB, так как точка O ∈ m, и OB = OC, так как O ∈ n. Тогда OA = OC, и, следовательно, O ∈ p.

Следствие 6.5.3.2. Около любого треугольника можно описать окружность, центром которой бу- дет точка пересечения серединных перпендикуляров к его сторонам. Такая окружность единственна.

59

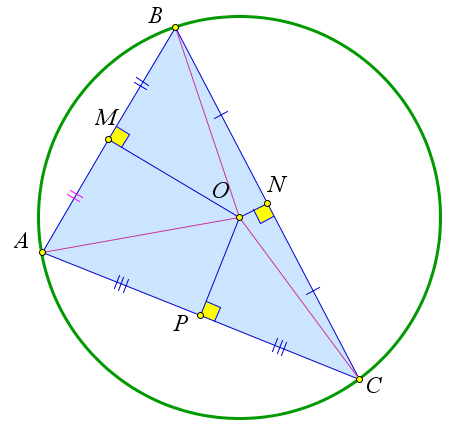
Доказательство.

Рис. 102. Следствие 6.5.3.2.

Рассмотрим треугольник ABC, в котором серединные перпендикуляры к сторонам пересекаются в точке O. Тогда точка O равноудалена от всех вершин треугольника, то есть OA = OB = OC. Тогда окружность с центром в точке O и радиусом OA будет описанной около данного треугольника.

Докажем, что такая окружность единственна. Предположим, что в треугольник можно вписать две окружности. Тогда, центры этих окружностей равноудалены от вершин треугольника. Но такая точка только одна – это точка пересечения серединных перпендикуляров. Кроме того их радиусы равны OA, следовательно эти окружности совпадают.

Следствие 6.5.3.3. Если все серединные перпендикуляры к сторонам выпуклого многоугольника пе- ресекаются в одной точке, то около него можно описать окружность, центром которой будет точка пересечения серединных перпендикуляров.

Доказательство.

Если все серединные перпендикуляры к сторонам выпуклого многоугольника пересекаются в одной точке, то эта точка равноудалена от всех его вершин, и, следовательно, окружность с центром в этой точке и с радиусом, равным расстоянию от этой точки до какой-либо из его вершин, будет описанной около этого многоугольника.

Теорема 6.5.4. Высоты треугольника (или их продолжения) пересекаются в одной точке.

Рис. 103. Теорема 6.5.4.

Доказательство.

Рассмотрим произвольный треугольник ABC, в котором проведены высоты AA₁,BB₁,CC₁ (рис. 103). Докажем, что все высоты пересекаются в одной точке.

Проведем через точку B прямую, параллельную AC, через точку C – прямую, параллельную AB, а через точку A – прямую, параллельную BC. Эти прямые, пересекаясь, образуют треугольник MNP. Четырёхугольник AMBC является параллелограммом (MB ∥ AC, MA ∥ BC). Аналогично, ABNC – параллелограмм. Тогда MB = AC = BN, как противоположные стороны параллелограмма. Следова- тельно, B – середина MN, а BB₁ – серединный перпендикуляр к отрезку MN. Аналогично, AA₁ – серединный перпендикуляр к отрезку MP, CC₁ – серединный перпендикуляр к отрезку PN. Получа- ется, что AA₁,BB₁ и CC₁ пересекаются в одной точке, как серединные перпендикуляры треугольника MNP.

Следствие 6.5.4.1. Если через вершины треугольника провести прямые, параллельные противопо- ложным сторонам, то пересекаясь, они образуют треугольник подобный исходному с коэффициен- том 2. При этом вершины исходного треугольника являются серединами сторон образовавшегося треугольника.

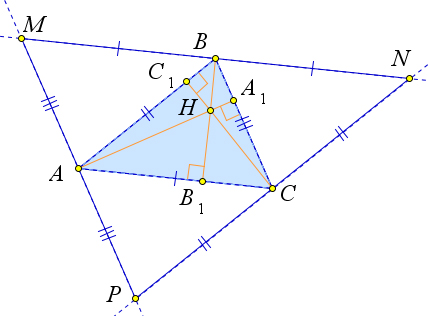
60

Следствие 6.5.4.2. Серединные перпендикуляры треугольника являются высотами серединного треугольника. Следовательно, ортоцентр серединного треугольника является центром окружно- сти, описанной около исходного треугольника.

Доказательство.

Утверждение полностью следует из доказательства теоремы 6.5.4.
Определение 6.11. Точка пересечения высот треугольника называется ортоцентром треугольника.

6.6 Вписанная и описанная окружности

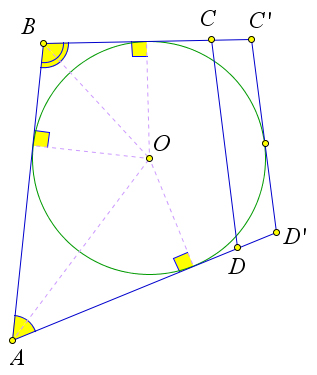
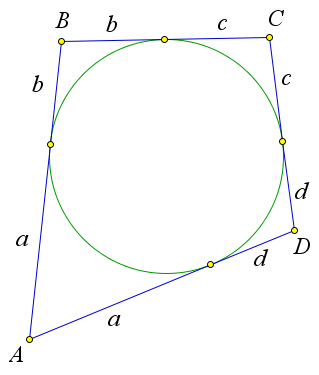
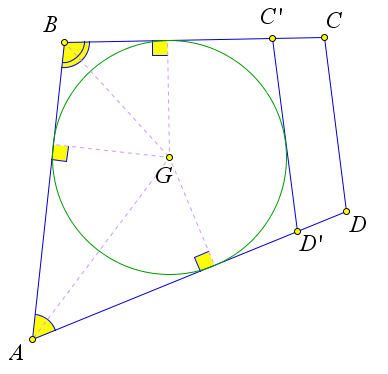
Теорема 6.6.1. В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

a)

Доказательство.

b)
Рис. 104. Теорема 6.6.1.

с)

Докажем, что если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны. Рассмотрим произвольный четырехугольник ABCD (рис. 104 a), в который вписана окружность. По пункту 2 теоремы 6.1.3 отрезки касательных, проведенных из одной точки равны. Обозначим равные отрезки буквами a,b,c и d. Тогда AD+BC =a+d+b+c=AB+CD.

Докажем, что если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность. Пусть в выпуклом четырёхугольнике ABCD

AB + CD = BC + AD. (1)

Точка O пересечения биссектрис углов A и B равноудалена от сторон AD,AB и BC, поэтому можно провести окружность с центром O, касающуюся указанных трёх сторон (рис. 104 b). Докажем, что эта окружность касается также стороны CD и, значит, является вписанной в четырёхугольник ABCD. Предположим, что это не так. Тогда прямая CD либо не имеет общих точек с окружностью, либо является секущей.

Рассмотрим первый случай (рис. 104 b). Проведем касательную C^′D^′, параллельную стороне CD (C^′ и D^′ – точки пересечения касательной со сторонами BC и AD). Так как ABC^′D^′ – описанный четырёхугольника, то AB+C^′D^′ = BC^′+AD^′. Но BC^′ = BC−CC^′,AD^′ = AD−DD^′, поэтому C^′D^′+C^′C+ D^′D = BC+AD−AB = CD. Таким образом C^′D^′+C^′C+D^′D = CD, то есть в четырёхугольнике C^′CDD^′ одна сторона равна сумме трех других сторон. Но этого не может быть, и, значит, предположение неверно.

Рассмотрим второй случай (рис. 104 c). Предположим, что прямая CD является секущей окружно- сти. Проведем касательную C^′D^′, параллельную стороне CD (C^′ и D^′ – точки пересечения касательной со сторонами BC и AD). Так как ABC^′D^′ – описанный четырёхугольника, то AB + C^′D^′ = BC^′ + AD^′. НоBC^′ =BC+CC^′,AD^′ =AD+DD^′.ТогдаAB+C^′D^′ =BC^′+AD^′ =BC+CC^′+AD+DD^′.Вычитая это равенство из равенства 1 получим AB+CD−AB−C^′D^′ =BC+AD−BC−CC^′ −AD−DD^′ или C^′D^′ = CD + CC^′ + DD^′. То есть в четырёхугольнике C^′CDD^′ одна сторона равна сумме трех других сторон. Но этого не может быть, и, значит, предположение неверно.

Следствие 6.6.1.1. В любой ромб можно вписать окружность.

61

Доказательство.

Так как у ромба все стороны равны, то и суммы противоположных сторон равны, и, следовательно, в ромб можно вписать окружность.

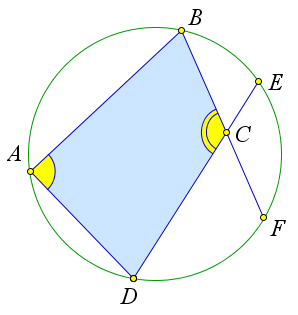
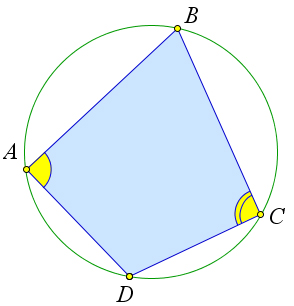
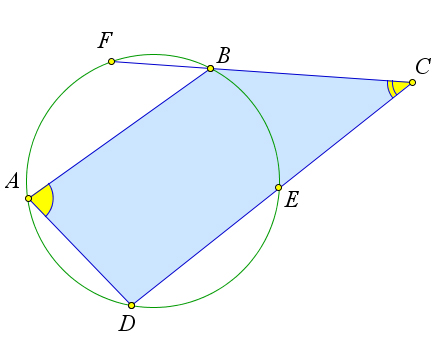
Теорема 6.6.2. Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180^○.

^a) b)
Рис. 105. Теорема 6.6.2.

Доказательство.

Рассмотрим произвольный вписанный четырехугольник ABCD (рис. 105 a). Углы A и C вписанные, поэтому _∠A = ¹ _􏰂BCD, _∠C = ¹ _􏰂BAD. Но так как _􏰂BCD + _􏰂BAD = 360^○, то _∠A + _∠C = ¹ (_􏰂BCD + _􏰂BAD) = 180^○.2 2 2

Докажем обратное. Пусть в произвольном четырёхугольнике ABCD сумма противоположных углов

_∠A+_∠C > ¹(_􏰂BED+_􏰂DAB)= ¹ ⋅360^○ =180^○. Итак _∠A+_∠C >180^○. Но это противоречит условию 1 22

c)

равна 180^○:

_∠A + _∠C = 180^○. (1)

Докажем, что такой четырёхугольник можно вписать в окружность. Заметим, что ABCD – выпуклый, так как в противном случае один из его углов был бы больше 180^○.

Проведём окружность через три вершины четырёхугольника: A, B и D (рис. 105 b). Это возможно, так как в силу следствия 6.5.3.2 около любого треугольника можно описать окружность. Докажем, что эта окружность проходит через вершину C. Предположим, что это не так. Тогда вершина C лежит либо внутри круга, либо вне его.

Рассмотрим первый случай (рис. 105 b). В этом случае можно продолжить стороны BC и DC

до пересечения с окружностью (получим соответственно точки F и E). Тогда по первому пункту

теоремы 6.3.2 _∠C = ¹ (_􏰂DAB + _􏰂EF ), и, следовательно, _∠C > ¹ _􏰂DAB. Так как _∠A = ¹ _􏰂BED, то 222

и, значит, предположение ошибочно.
Рассмотрим второй случай. Пусть вершина C лежит вне круга. Тогда прямые BC и CD являются

либо секущими, либо касательными к данной окружности. Пусть они пересекают окружность в точках

F и E соответственно. Пусть точка F лежит на дуге AB, а точка E на дуге BD (остальные случаи

расположения точек F и E доказываются аналогично). В этом случае по второму пункту теоремы

6.3.2 _∠C = ¹ (_􏰂BAD − _􏰂BE), и, следовательно, _∠C < ¹ _􏰂BAD. Так как _∠A является вписанным, то 22

_∠A = ¹ _􏰂BED. Тогда _∠A + _∠C < ¹ (_􏰂BAD + _􏰂BED) < ¹ ⋅ 360^○ = 180^○. Но это противоречит условию 1 222

и, значит, предположение ошибочно.

Следствие 6.6.2.1. Около трапеции можно описать окружность тогда и только тогда, когда тра- пеция равнобедренная.

Доказательство.

Рассмотрим равнобедренную трапецию ABCD. Докажем, что около неё можно описать окруж- ность. Действительно, так в равнобедренной трапеции _∠A + _∠B = 180^○,_∠B = _∠C, следовательно, _∠A + _∠C = 180^○, то есть сумма противоположных углов равнобедренной трапеции равна 180^○, и сле- довательно по теореме 6.6.2 около неё можно описать окружность.

Докажем, что если около трапеции можно описать окружность, то эта трапеция равнобедренная. Рассмотрим трапецию ABCD, около которой можно описать окружность. Тогда по теореме 6.6.2 _∠A+ _∠C = 180^○. Кроме того _∠A+_∠B = 180^○. Следовательно, _∠C = _∠B, и, значит, трапеция равнобедренная.

62

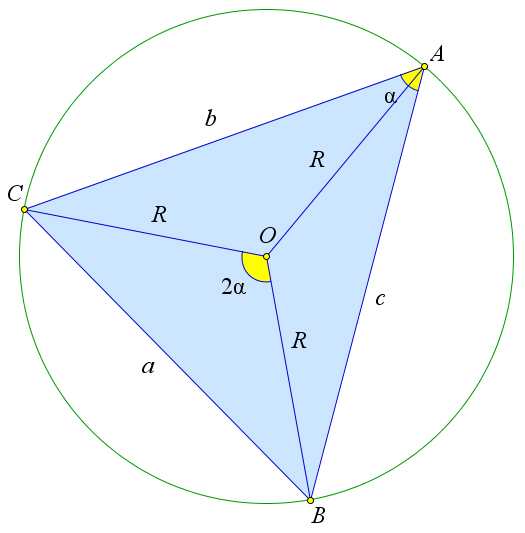
Теорема 6.6.3 (Обобщенная теорема синусов). В треугольнике со сторонами a,b,c, углами α,β,γ и

радиусом описанной окружности R выполняется соотношение 2R =

^a) b)
Рис. 106. Теорема 6.6.3.

Доказательство.

^a = ^b = ^c . sinα sinβ sinγ

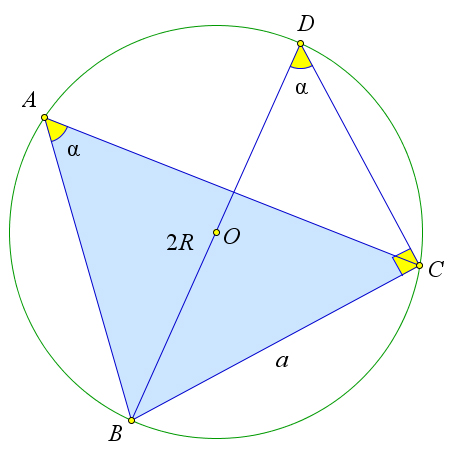
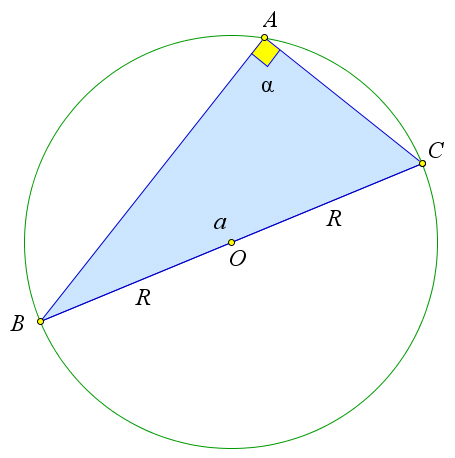
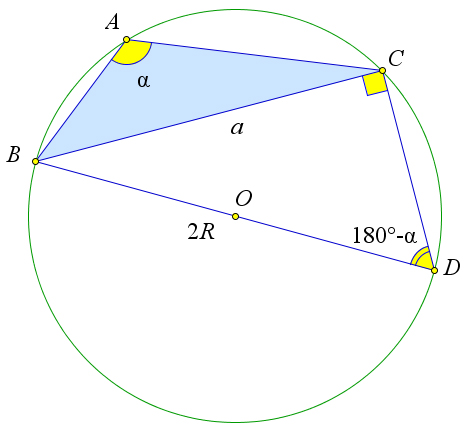
Рассмотрим треугольник ABC, около которого описана окружность с центром O и радиусом R. Обозначим a = BC, α = _∠A. Докажем, что ^BC = 2R или 2R = ^a . Возможны три случая: когда угол

sin _∠A sin α

c)

α прямой, острый или тупой.
Рассмотрим первый случай, когда угол A прямой (рис. 106 a). Так как вписанный угол равный 90^○

опирается на диаметр, то BC =2R. Но так как sinA=sin90^○ =1, то BC =2R⋅1=BCsinα. Рассмотрим второй случай, когда угол A – острый (рис. 106 b). Проведем диаметр BD и рассмотрим треугольник DBC. Так как углы A и D опираются на одну и туже дугу BC, то _∠A = _∠D. Кроме того, угол BCD опирается на диаметр, следовательно, _∠BCD = 90^○. Тогда из прямоугольного треугольника

BCDsinD=^BC или2R= ^BC . 2R sinA

Рассмотрим третий случай, когда угол A – тупой (рис. 106 c). Проведем диаметр BD и рассмотрим треугольник DBC. Так как угол A опирается на дугу BDC, а угол D опирается на дугу BAC, то _∠D = 180^○ − _∠A. Кроме того, угол BCD опирается на диаметр, следовательно, _∠BCD = 90^○. Тогда из прямоугольного треугольника BCD sin D = ^BC = sin (180^○ − _∠A) = sin A или 2R = ^BC .

2R sinA
Следствие 6.6.3.1. Радиус окружности, описанной около треугольника удовлетворяет соотноше-

нию R = ^abc . 4S

Доказательство.

^a . Кроме того S = ¹ bc sin α, откуда sin α = ^2S . Подставляя это выражение sinα 2 bc

По теореме 6.6.3 2R =
для sin α в формулу для радиуса, получим 2R = ^a или R = ^abc .

2S bc

влетворяет соотношению S = pr, где S – площадь многоугольника, а p – его полупериметр.

Доказательство.

Рассмотрим n-угольник A₁A₂A₃ . . . A_n, в который вписана окружность с центром O и радиусом r. Соединим вершины многоугольника с центром окружности и получим n треугольников, в каждом из которыхвысотойявляетсярадиусвписаннойокружности.ТогдаS=S_A1OA2 +S_A2OA3 +...+S_{An_1OAn} =

¹rA₁A₂ + ¹rA₂A₃ +...+ ¹rA_n−1A_n = ¹r(A₁A₂ +...+A_n−1A_n)=pr. 2222

Теорема 6.6.5. Радиус окружности, вписанной в треугольник, и его высоты связаны соотношением ¹=¹+¹+¹.

Доказательство.

Так как площадь треугольника равна полупроизведению высоты и стороны, к которой эта высота проведена, то можно выразить стороны следующим образом: a = ^2S , b = ^2S , c = ^2S . Кроме того, так как

¹=¹+¹+¹. r h_a h_b h_c

Теорема 6.6.6. Инцентр делит биссектрису l_c треугольника в отношении ^a+b , где a, b и c – стороны c

треугольника.

4S
Теорема 6.6.4. Радиус окружности, вписанной в многоугольник (в частности, в треугольник) удо-

r h_a h_b h_c

^ha ^hb ^hc
S = pr, то a+b+c = 2p = ^2S. Тогда, складывая первые три равенства, получим ^2S + ^2S + ^2S = ^2S или

r abcr

63

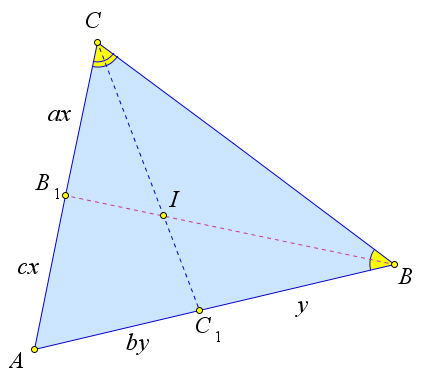
Доказательство.

Рис. 107. Теорема 6.6.6.

Рассмотрим треугольник ABC со сторонами a,b и c, в котором проведены биссектрисы BB₁ и

CC₁ (рис. 107). Докажем, что точка пересечения биссектрис I делит биссектрису CC₁ в отношении CI ₌a+b_.

IC1 c
По теореме 3.3.2 ^AB1 = ^c , ^AC1 = ^b . Тогда по теореме Менелая для треугольника ACC₁ и секущей

B₁C aC₁B a B₁Bполучаем^AB1⋅^CI⋅^C1B=^c⋅^CI⋅^a =1,откуда^CI=^a+b.

B₁C IC₁ BA a IC₁ a+b IC₁ c
Теорема 6.6.7. Если M – точка касания со стороной AC окружности, вписанной в треугольник

ABC, то AM = p − BC, где p – полупериметр треугольника.

Рис. 108. Теорема 6.6.7.

Доказательство.

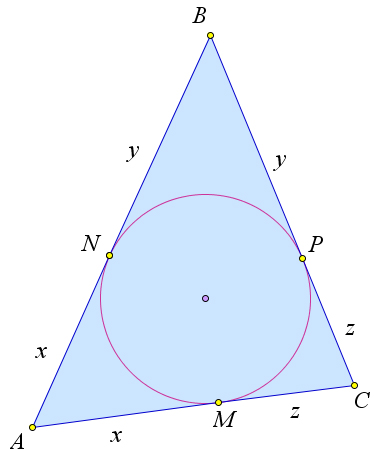
Рассмотрим треугольник ABC, в который вписана окружность. Пусть окружность касается сторон A, AB и BC в точках M, N и P соответственно. Докажем, что AM = p − BC.

Так как касательные к окружности, проведённые из одной точки равны, то можно обозначить x=AM=AN,y=BN=BP,z=CM=CP.ТогдаAM=x=^2x+2y+2z −(y+z)=p−(y+z)=p−BC.

2

Теорема 6.6.8.

1. Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле r = a+b−c _.

2

2. Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотену- зы, а её центр совпадает с серединой гипотенузы.

64

Доказательство.

a)

Рис. 109. Теорема 6.6.8.

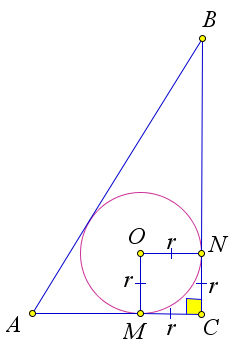
Докажем первый пункт теоремы. Рассмотрим треугольник ABC с прямым углом C. Пусть в него вписана окружность с центром O и радиусом r, которая касается катетов AC и BC в точках M и N соответственно (рис. 109 a). Тогда MONC – квадрат, так как все его углы прямые и MO = ON = r. ТогдаCM=r.Нопотеореме6.6.7CM=p−c=^a+b+c −c,тоестьr=^a+b−c.

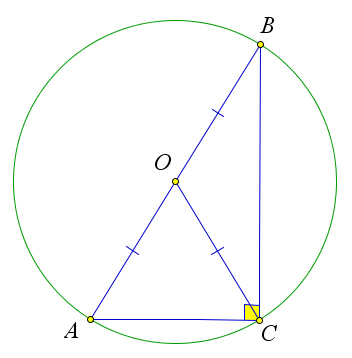
Докажем второй пункт теоремы. Рассмотрим треугольник ABC с прямым углом C. Пусть O – сере- дина гипотенузы AB (рис. 109 b). Тогда по теореме 1.6.2 OA = OB = OC, то есть точка O равноудалено от всех вершин треугольника. Следовательно, точка O является центром окружности, описанной около треугольника ABC, радиус которой равен OA, то есть половине гипотенузы.

Теорема 6.6.9 (Теорема Птолемея). Около четырехугольника можно описать окружность тогда и только тогда, когда произведение его диагоналей равно сумме произведений его противоположных сторон.

b)

22

Доказательство.

a)

b)

Рис. 110. Теорема 6.6.9.

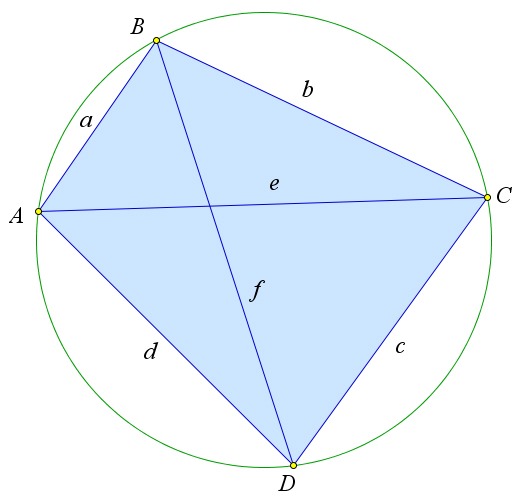
Рассмотрим четырёхугольник ABCD вписанный в окружность (рис. 110 a). Тогда _∠ABC+_∠ADC =

180^○, тогда косинусы этих углов противоположны. Тогда cos _∠ABC + cos _∠ADC = 0. Из треуголь-

ников ABC и ADC по теореме косинусов имеем cos_∠ABC = ^a2^+b2^−e2 ,cos_∠ADC = ^d2^+c2^−e2 . Сумма 2ab 2dc

этих косинусов равна нулю, то есть ^a2^+b2^−e2 + ^d2^+c2^−e2 = 0. a²dc + b²dc − e²dc + d²ab + c²ab − e²ab = 0. 2ab 2dc

e² = ^ab(d2^+c2^)+dc(a2^+b2⁾ = ^{(ac+bd)(ad+bc)}. Аналогично из треугольников ABD и BCD выразим f²: ab+dc ab+cd

f² = ^{(ab+cd)(ac+bd)}. Отсюда (ef)² =(ac+bd)², откуда ef =ac+bd. ad+bc

Обратно. Пусть выполнено равенство AB⋅CD+BC⋅AD = AC⋅BD (рис. 110 b). Докажем, что тогда около четырёхугольника ABCD можно описать окружность.

Обозначим через R радиус окружности, описанной около треугольника ABC. Из точки D опустим перпендикуляры на прямые AB,BC и AC и обозначим точки пересечения этих прямых и перпендику- ляров к ним через C₁,A₁ и B₁ соответственно. По теореме синусов для треугольника A₁CB₁ получаем (диаметр описанной окружности для этого треугольника равен CD):

A₁B₁ =CDsin_∠A₁CB₁ =CDsin_∠BCA. 65

По теореме синусов для треугольника ABC имеем AB = 2Rsin_∠BCA. Следовательно, A₁B₁ = ^CD⋅AB. Таким же образом, рассматривая треугольники B₁CC₁ и A₁CC₁, получим соотношения

2R
B₁C₁ = ^BC⋅AD , A₁C₁ = ^AC⋅BD . Отсюда, подставляя эти выражения в исходное равенство, имеем

2R 2R
2R(A₁B₁ + B₁C₁) = C₁A₁ ⋅ 2R, или C₁A₁ = A₁B₁ + B₁C₁, откуда следует, что точки A₁, B₁ и C₁ ле-

жат на одной прямой. Докажем теперь, что из этого следует, что вокруг четырёхугольника ABCD можно описать окружность. Построим окружности на отрезках AD и CD как на диаметрах. Первая из них проходит через точки B₁ и C₁ (углы AB₁D и AC₁D прямые), а вторая – через точки A₁ и B₁ (_∠CB₁D = _∠CA₁D = 90^○). Углы AB₁C₁ и A₁B₁C равны, как вертикальные, откуда следует, что _∠ADC₁ = _∠CDA₁, а значит, и _∠DAC₁ = _∠DCA₁. Отсюда _∠DAB + _∠DCB = 180^○, и, следовательно, около четырёхугольника ABCD можно описать окружность.

Следствие 6.6.9.1. Площадь вписанного четырехугольника, диагонали которого перпендикулярны вычисляется по формуле S = ^ac+bd .

2

Доказательство.

По теореме 5.1.4 площадь четырёхугольника выражается через диагонали по формуле S = ¹d₁d₂sinφ. Но так как φ = 90^○, то есть sinφ = 1, а по теореме Птолемея d₁d₂ = ac+bd, то

2

S = ¹d₁d₂ sinφ = ^ac+bd. 22

Теорема 6.6.10 (Формула Брахмагупты). Пусть a,b,c,d – стороны вписанного в окружность че- тырехугольника, p – его полупериметр, а S – его площадь. Тогда S = ^√(p − a)(p − b)(p − c)(p − d).

Доказательство.

Рассмотрим вписанный четырёхугольник ABCD со сторонами AB = a,BC = b,CD = c,DA = d. По теореме косинусов для треугольников ABC и ACD: AC² = a² + b² − 2ab cos B, AC² = c² + d² − 2cd cos D. Приравняв правые части этих равенств, получим: a² + b² − 2ab cos B = c² + d² − 2cd cos D. Так как четырёхугольник ABCD вписанный, то _∠B = 180^○ −_∠D, следовательно, cosD = −cosB. Тогда a² + b² − 2ab cos B = c² + d² + 2cd cos B. Возведя это равенство в квадрат, получим

(a² +b² −c² −d²)² =4cos²B(ab+cd)². (1) Кроме того S = S_ABC + S_ACD = ¹ ab sin B + ¹ cd sin D. Умножив это равенство на 4 и возведя в квадрат,

22
получим16S² =4a²b²sin²B+8abcdsinBsinD+4c²d²sin²D.Атаккак_∠B=180^○−_∠D,тоsinB=sinD.

Тогда16S² =4a²b²sin²B+8abcdsinBsinB+4c²d²sin²B=4sin²B(a²b²+2abcd+c²d²)=4sin²B(ab+cd)².

Таким образом

16S² =4sin²B(ab+cd)². (2)

Складывая равенства (1) и (2), получим 16S² +(a² +b² −c² −d²)² = 4sin² B(ab+cd)² +4cos² B(ab+cd)² = 4(ab+cd)²(sin²B+cos²B)=(2ab+2cd)² или16S² =(2ab+2cd)²−(a²+b²−c²−d²)² =(2ab+2cd+a²+b²− c² −d²)(2ab+2cd−a² −b² +c² +d²) = ((a+b)² −(c−d)²)((c+d)² −(a−b)²) = (a+b−c+d)(a+b+c−d)(c+d+ a−b)(c+d−a+b) = (2p−2c)(2p−2d)(2p−2b)(2p−2a). Откуда следует, что S² = (p−a)(p−b)(p−c)(p−d) или S = ^√(p − a)(p − b)(p − c)(p − d).

6.7 Вневписанные окружности

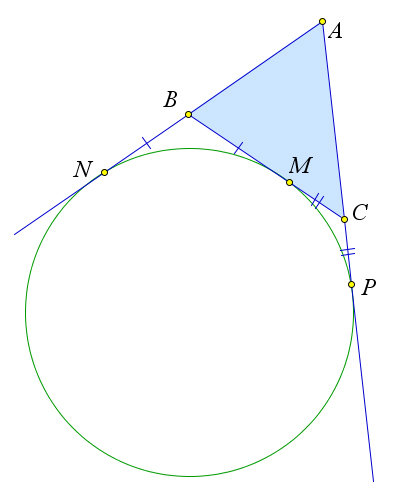
Определение 6.12. Окружность, касающаяся стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью этого треугольника.

Теорема 6.7.1. У любого треугольника есть три вневписанных окружности.

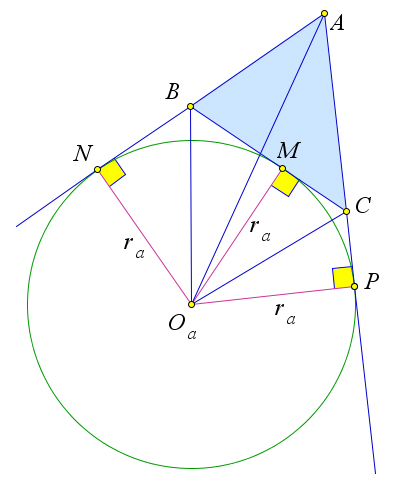
Доказательство.

Рассмотрим треугольник ABC. Пусть биссектрисы внешних углов при вершинах B и C пересека- ются в точке O_a. Тогда точка O_a равноудалена от прямых AB,BC и AC, следовательно, точка O_a лежит на биссектрисе угла A, и окружность с центром в точке O_a и радиусом r_a, равным расстоянию от точки O_a до стороны BC, касается стороны BC и продолжений сторон AB и AC, то есть явля- ется вневписанной окружностью данного треугольника. Аналогично можно построить вневписанные окружности с центрами в точках O_b и O_c, касающиеся сторон AC и BA соответственно.

Теорема 6.7.2 (свойства вневписанной окружности).

1^○ Пусть в треугольнике ABC биссектриса AA₁ пересекается с окружностью, описанной около этого треугольника, в точке D. Точка D является центром окружности, описанной около четырёхугольника BOCO_a, где O – центр окружности, вписанной в треугольник ABC, а O_a – центр вневписанной окружности.

66

Доказательство.

Точка O, как центр окружности, вписанной в треугольник ABC, лежит на биссектрисе угла B, а точка O_a, как центр вневписанной окружности лежит на биссектрисе угла, смежного с углом B. По утверждению 1.4.3 биссектрисы смежных углов перпендикулярны, следовательно _∠OBO_a = 90^○. Аналогично _∠OCO_a = 90^○. Следовательно, по теореме 6.6.2 около четырёхугольника BOCO_a можно описать окружность.

Пусть продолжение биссектрисы AA₁ и BB₁ пересекают окружность, описанную около треуголь-

ника ABC в точке D и E. Так как AD и BE – биссектрисы, то _􏰂BD = _􏰂DC,_􏰂AE = _􏰂EC.

Обозначим эти пары углов соответственно α и β. Тогда _∠EBD = ^α+β , так как он вписанный, а 2

_∠BOD=^α+β всилупервогопунктатеоремы6.3.2.Следовательно,втреугольникеBODуглыпри 2

основании BOD равны, то есть он равнобедренный BD = DO. Таким образом BD = DO = OC.

Таким образом точка D равноудалена от всех вершин треугольник BOC, и, следовательно, яв- ляется центром окружности, описанной около этого треугольника. Но эта окружность является также окружностью, описанной около четырёхугольника BOCO_a.

• 2^○  Точки, в которых вписанная и вневписанная окружности касаются стороны треугольника, сим- метричны относительно середины этой стороны. 
Доказательство. 
Рассмотрим треугольник ABC. Пусть вневписанная окружность ω_a(O_a,r_a) и вписанная окруж- ность ω(O,r) касаются стороны BC в точках P и Q. Докажем, что точки P и Q симметричны относительно точки M – середины стороны BC. 
Пусть точка D – это точка пересечения продолжения биссектрисы AA₁ с описанной окружностью. По первому свойству D – это центр окружности, описанной около четырехугольника BOCO_a. Следовательно, точка D лежит на серединном перпендикуляре к стороне BC, то есть точка D проецируется в точку M. Кроме того, так как O_aD = DO, то по теореме Фалеса PM = MQ (так как радиусы проведенные в точку касания перпендикулярны касательной BC и DM - серединный перпендикуляр к BC, то O_aP ∥ DM ∥ OQ).

• 3^○  Прямая, проведенная через вершину треугольника и точку, в которой вневписанная окруж- ность касается противоположной стороны, делит периметр треугольника пополам. Длина отрезка касательной, проведённой к вневписанной окружности из противоположной вершины, равна полупериметру треугольника. 
Рис. 111. Теорема 6.7.2. Свойство 3. 
Доказательство. 
Рассмотрим треугольник ABC. Пусть вневписанная окружность ω_a касается прямых AB,BC и AC в точках N,M и P соответственно. Докажем, что AB+BM =AC+MC (рис. 111). 
Действительно, так как касательные, проведенные к окружности из одной точки равны, то AN = AP,BN =BM и CM =CP. Учитывая эти соотношения, получаем AB+BM =AB+BN =AN = AP =AC+CP =AC+CM. Таким образом AN =AB+BN =p.

67

4^○ S=r_a(p−a).

Доказательство.

Рис. 112. Теорема 6.7.2. Свойство 3.

Рассмотрим треугольник ABC. Пусть ω_a(O_a, r_a) – вневписанная окружность этого треугольника, а a, b, c – его стороны (рис. 112). Докажем, что S = r_a(p − a).

Пусть N, M, P – это точки касания окружности ω_a и прямых AB, BC и AC соответственно.

Соединим центр вневписанной окружности O_a с вершинами треугольника. Тогда S_ABC = S_ABOa +

S −S =¹r c+¹r b−¹r a=r ^b+c−a =r (p−a). ACO_a BCO_{a 2}a ₂a ₂a a₂ a

• 5^○  S = ^√rr_ar_br_c. Доказательство. 
По свойству 4^circ S = r_a(p−a),S = r_b(p−b),S = r_c(p−c). Кроме того S = rp. Тогда p = 
S= p(p−a)(p−b)(p−c)=

• ₆○  _S=^ra^rb^rc_. 
p 
Доказательство. 
По свойству 4^circ S = r_a(p − a), S = r_b(p − b), S = r_c(p − c). Тогда p = ^S , p − a = ^S , p − b = ^S , p − c = ^S .

^S,p−a = ^S ,p−b = ^S ,p−c = ^S . Подставляя эти соотношения в формулу Герона, получим ^r _√ ^ra ^rb _√ ^rc

4²√
^S =^{√ S} ,илиS= rr_ar_br_c.

rr_a r_b r_c rr_a r_b r_c

_√r ra r_b√rc Подставляя эти соотношения в формулу Герона, получим S = p(p − a)(p − b)(p − c) = ^S3^p

.

Возводя это равенство в квадрат и выражая S, получим S = ^rarbrc . p

7^{○ 1} = ¹ + ¹ + ¹ . r r_a r_b r_c

Доказательство.

^ra^rb^rc

Напишем цепочку равенств, учитывая свойство 4^○, ¹ + ¹ + ¹ = ^p−a + ^p−b + ^p−c = ^{3p−a−b−c} =

3a+3b+3c−2a−2b−2c ₌ a+b+c ₌ ^p ₌ 1 _. 2S 2SSr

8^○ r_ar_b =p(p−c),rr_a =(p−b)(p−c). Доказательство.

По свойству 4^○, учитывая формулу Герона, r r = a b

_S² ₌ p(p−a)(p−b)(p−c) _{= (p − b)(p − c).} p(p−a) p(p−a)

r_a r_b r_c S S S S

_S² ₌ p(p−a)(p−b)(p−c) _{= p(p − c), rr =} (p−a)(p−b) (p−a)(p−b) ^a

9^○ Исходный треугольник является ортотреугольником треугольника O_a O_b O_c .

68

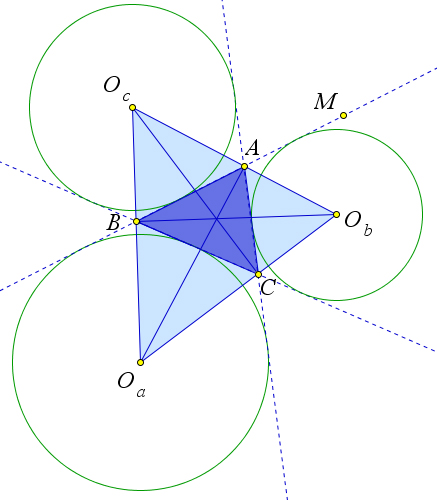
Доказательство.

Рис. 113. Теорема 6.7.2. Свойство 8.

Достаточно доказать, что биссектриса AO_a угла A является высотой треугольника O_aO_bO_c, то есть нужно доказать, что _∠O_aAO_c = 90^○ (рис. 113).

Отрезки AO_a и AO_b являются биссектрисами смежных углов _∠BAC и _∠CAM, следовательно, по утверждению 1.4.3 _∠O_aAO_c. Аналогично BO_b и CO_c являются высотами треугольника O_aO_bO_c.

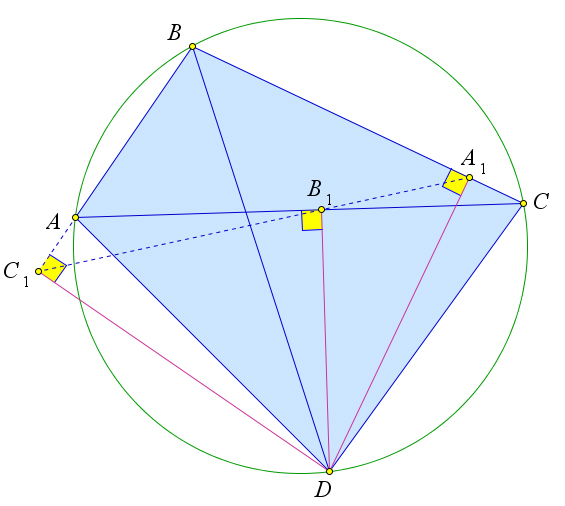
10^○ 4R=r_a +r_b +r_c −r. 6.8 Ортоцентр

Теорема 6.8.1 (об ортоцентрической системе точек). Если в четвёрке точек A,B,C,H точка H является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками.

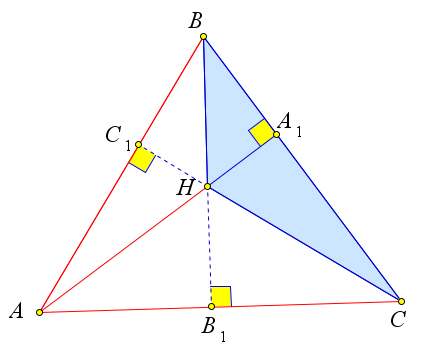
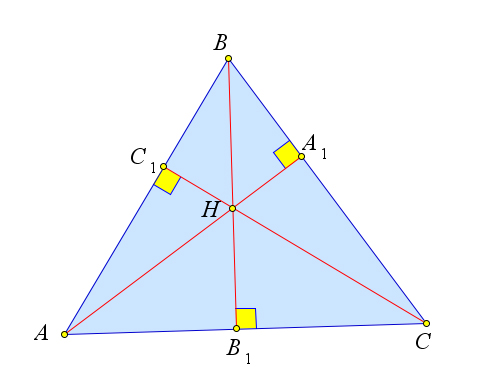
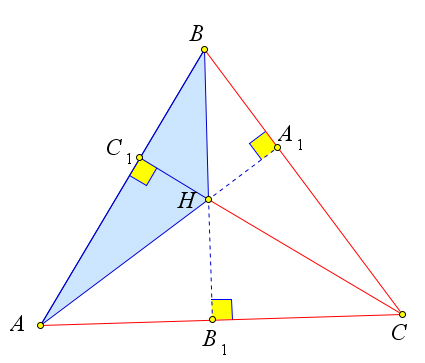
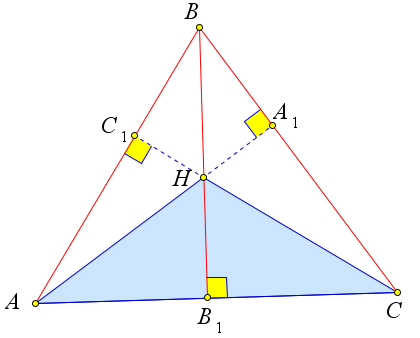
a)

c)

b)

d)

Доказательство.

Рис. 114. Теорема 6.8.1.

Рассмотрим треугольник ABC, в котором AA₁,BB₁,CC₁ – это высоты, точка H – это ортоцентр (рис. 114 a). Докажем, что точка A – это ортоцентр треугольника BCH.

Действительно, для треугольника BCH высотами являются BC₁,HA₁ и B₁C (рис. 114 b). А пря- мые, содержащие эти отрезки, пересекаются в точке A. Аналогично на рисунках 114 c и 114 d видно, что точки B и C являются ортоцентрами для треугольников ACH и ABH соответственно.

Теорема 6.8.2. Радиусы окружностей, проходящих через любые три точки ортоцентрической си- стемы, равны.

69

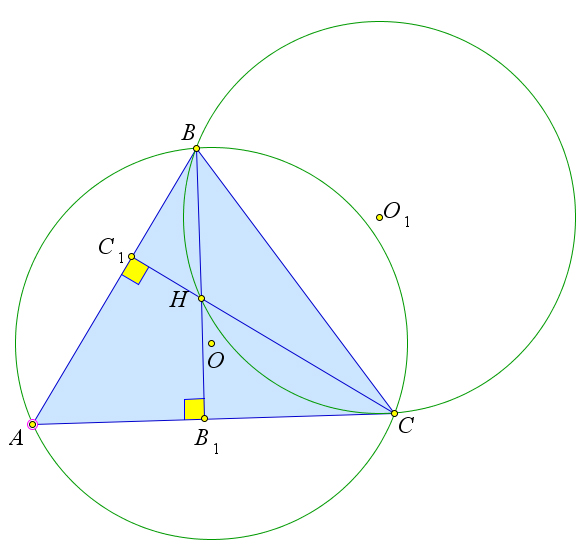
Доказательство.

Рис. 115. Теорема 6.8.2.

Рассмотрим треугольник ABC, в котором высоты BB₁ и CC₁ пересекаются в точке H. Докажем,

что радиусы окружностей ω и ω₁, описанных соответственно около треугольников ABC и BCH, равны.

В четырёхугольнике AC₁HB₁ углы C₁ и B₁ прямые. А так как сумма углов четырёхугольника

равна 360^○, то _∠CHB = 180^○ −_∠A, и, следовательно, синусы этих углов равны. По теореме ?? радиусы

рассматриваемых окружностей выражаются по формулам R = ^BC ,R = ^BC . Но так как

2sin_∠A ¹ 2sin_∠CHB
Теорема 6.8.3. В остроугольном треугольнике ABC с высотами AA₁,BB₁,CC₁ выполняются сле-

синусы _∠A и _∠CHB равны, то и радиусы R и R₁ равны.

дующие соотношения: 1. _∠A₁AC = _∠B₁BC, 2. _∠C₁CB = _∠A₁AB, 3. _∠B₁BA = _∠C₁CA.

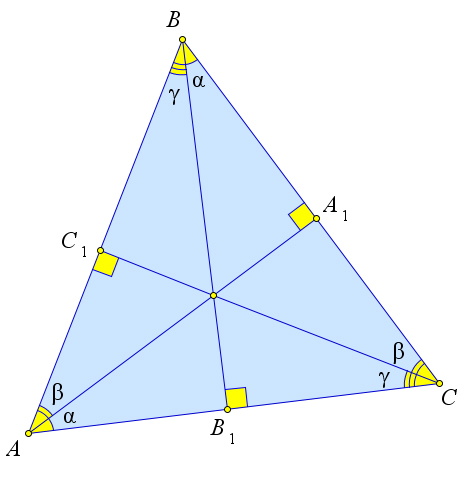
Доказательство.

Рис. 116. Теорема 6.8.3.

Рассмотрим треугольник ABC с высотами AA₁,BB₁,CC₁.

В прямоугольных треугольниках AA₁C и BB₁C острый угол C является общим, поэтому другие острые углы равны: _∠A₁AC = _∠B₁BC.

Аналогично в треугольниках A₁AB и C₁CB есть общий острый угол B, а в треугольниках B₁BA и C₁CA есть общий острый угол A, следовательно, другие острые углы в этих парах треугольников равны между собой: _∠C₁CB = _∠A₁AB, _∠B₁BA = _∠C₁CA.

Теорема 6.8.4. В остроугольном треугольнике ABC с высотами AA₁,BB₁,CC₁ и ортоцентром H выполняются следующие соотношения:

1. _∠A = _∠B₁HC = _∠C₁HB = _∠B₁A₁C = _∠C₁A₁B, 2. _∠B = _∠A₁HC = _∠C₁HA = _∠C₁B₁A = _∠A₁B₁C, 3. _∠C = _∠B₁HA = _∠A₁HB = _∠B₁C₁A = _∠A₁C₁B.

70

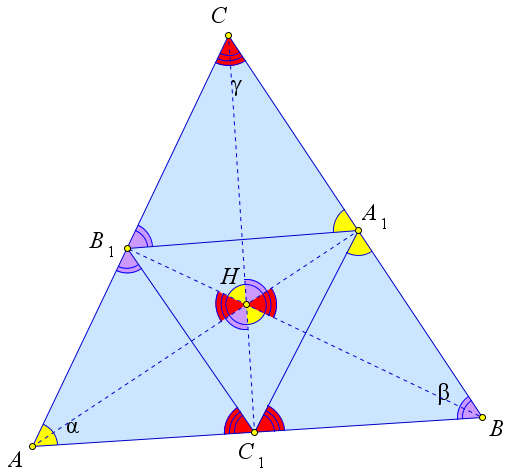
Доказательство.

Рис. 117. Теорема 6.8.4.

Обозначим α = _∠A,β = _∠B,γ = _∠C. В прямоугольных треугольниках ACC₁ и CB₁H есть общий острый угол _∠ACC₁, следовательно, другие острые углы в этих треугольниках равны: _∠A = _∠B₁HC = α. Кроме того _∠C₁HB = _∠B₁HC = α, как вертикальные.

По теореме 6.8.3 _∠CAA₁ = _∠B₁BC. Выпишем синусы этих углов из прямоугольных треуголь- ников CAA₁ и BB₁C: sin_∠CAA₁ = ^A1C , sin_∠B₁BC = ^B1C , значит, ^A1C = ^B1C или ^A1C = ^AC .

AC BC AC BC B₁C BC Тогда _△A₁B₁C ∼ _△ABC по второму признаку подобия (угол C – общий, а стороны CA₁ и CB₁

пропорциональны сторонам CA и CB). Тогда углы этих треугольников, лежащие напротив про- порциональных сторон, равны: _∠CA₁B₁ = _∠A = α,_∠CB₁A₁ = _∠B = β. Аналогично из подобия треугольников A₁BC и ABC получаем _∠BA₁C₁ = _∠A = α,_∠BC₁A₁ = _∠C = γ. Таким образом _∠A = _∠B₁HC = _∠C₁HB = _∠B₁A₁C = _∠C₁A₁B. Аналогично можно получить и остальные соотно- шения.

Теорема 6.8.5. В остроугольном треугольнике ABC с высотами AA₁,BB₁,CC₁ и ортоцентром H выполняются следующие соотношения:

1. _∠B₁BC = _∠CC₁A₁ = _∠CC₁B₁ = _∠A₁AC = α, 2. _∠BAA₁ = _∠C₁B₁B = _∠A₁B₁B = _∠C₁CB,
3. _∠ABB₁ = _∠C₁A₁A = _∠AA₁B₁ = _∠ACC₁.

Рис. 118. Теорема 6.8.5.

Доказательство.

Рассмотрим треугольник ABC, в котором проведены высоты AA₁,BB₁,CC₁, а точка H является ортоцентром.

По теореме 6.8.4 _∠AC₁B = _∠BC₁A₁ = _∠C. Тогда, так как _∠CC₁A = 90^○, то _∠CC₁B₁ = 90^○ − _∠C = _∠A₁C₁C. C другой стороны, из прямоугольного треугольника AA₁C получаем, что _∠A₁AC = 90^○ −_∠C, значит, _∠A₁AC = _∠CC₁B₁ = _∠CC₁A₁. Аналогично можно получить и остальные соотношения.

Следствие 6.8.5.1. Высоты треугольника являются биссектрисами его ортотреугольника (следо- вательно, ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).

Теорема 6.8.6. Пусть AA₁,BB₁ и CC₁ – высоты треугольнике ABC, а H – ортоцентр этого треугольника. Тогда

1. _△ABC ∼ _△AC₁B₁ ∼ _△BC₁A₁ ∼ _△CB₁A₁.
71

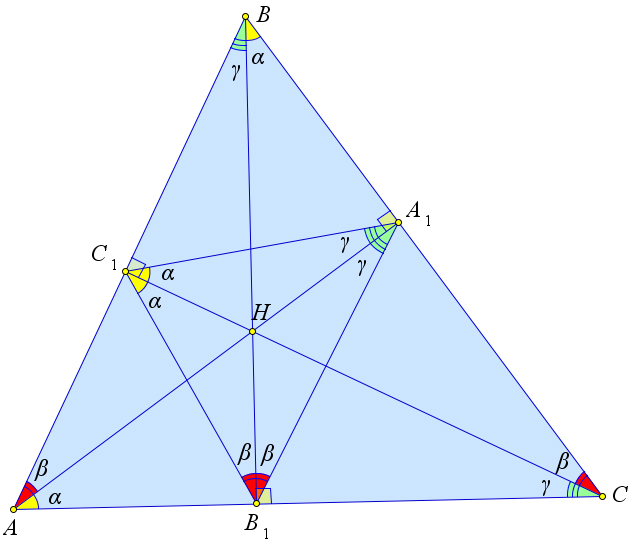
2. _△BCH ∼ _△B₁C₁H, _△ABH ∼ _△A₁B₁H, _△ACH ∼ _△A₁C₁H.

3. _△BC₁H ∼ _△B₁CH ∼ _△BAB₁ ∼ _△CC₁A, _△BA₁H ∼ _△AB₁H ∼ _△BB₁C ∼ _△AA₁C, _△AC₁H ∼ _△A₁HC ∼ _△ABA₁ ∼ _△CC₁B.

Доказательство.

С учётом первого признака подобия треугольников первый пункт теоремы напрямую следует из теоремы 6.8.4, а второй пункт теоремы напрямую следует из теоремы 6.8.5.

В третьем пункте теоремы _△BCH ∼ _△B₁CH по второму признаку подобия, так как _∠HBC₁ = _∠B₁CH по теореме 6.8.3, а _∠C₁HB = _∠B₁HC, как вертикальные. Подобие прямоугольных треуголь- ников BC₁H и ABB₁ следует из того, что острый угол ABB₁ для этих треугольников является общим. Остальные подобия доказываются аналогично.

Теорема 6.8.7. Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.

Рис. 119. Теорема 6.8.7.

Доказательство.

Рассмотрим треугольник ABC, в котором высоты BB₁ и AA₁ пересекаются в точке H. Пусть прямая AA₁ пересекает окружность, описанную около треугольника ABC, в точке D. Докажем, что точка D симметрична точке H относительно стороны BC. Так как HD ⊥ BC, то достаточно доказать, что HA₁ = A₁D.

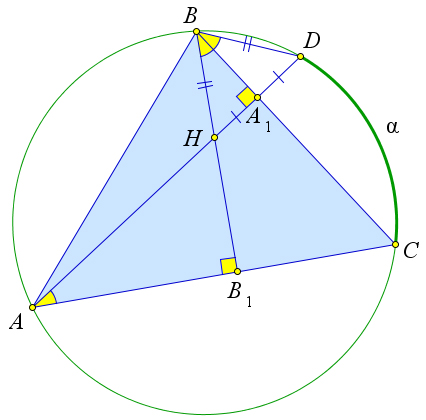
Пусть _􏰂DC = α. Тогда _∠DAC = _∠DBC = ^α , так как это вписанные углы. Кроме того, так как в 2

прямоугольных треугольниках AHB₁ и BHA₁ острые углы _∠AHB₁ и _∠BHA₁ равны, то другие острые углы тоже равны, то есть _∠HAC = _∠HBC = ^α. Тогда в треугольнике HBD отрезок BA₁ является

2
биссектрисой и высотой, значит, _△BHD – равнобедренный, а BA₁ не только высота и биссектриса, но

и медиана, то есть HA₁ = A₁D.

Теорема 6.8.8. Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противополож- ными соответствующим вершинам.

72

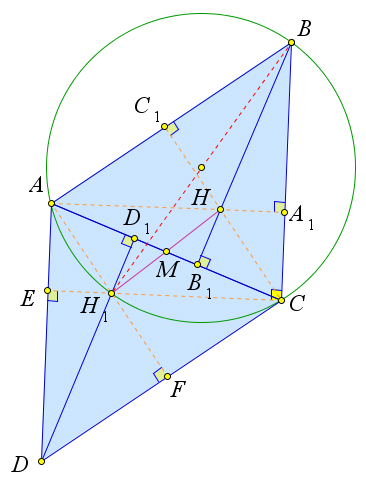
Доказательство.

Рис. 120. Теорема 6.8.8.

Рассмотрим треугольник ABC, в котором высоты AA₁,BB₁,CC₁ пересекаются в точке H. Дока- жем, что точка H₁, симметричная точке H относительно середины M стороны AC, лежит на окруж- ности, описанной около треугольника ABC, при этом H₁B – это диаметр.

Рассмотрим центральную симметрию треугольника ABC относительно точки M. Пусть точка D – это образ точки B при такой симметрии, тогда треугольник ABC отображается в треугольник CAD, а точка H, ортоцентр треугольника ABC, отображается в точку H₁, ортоцентр треугольника CAD. Нужно доказать, что точка H₁ лежит на окружности, описанной около треугольника ABC.

Углы B и D равны (так как симметричные треугольники ABC и CAD равны). Кроме того, так как в четырёхугольнике DEH₁F углы E и прямые, то _∠AH₁F = 180^○ − _∠D = 180^○ − _∠B. Таким образом _∠AH₁C + _∠B = 180^○. Таким образом в четрёхугольнике ABCH₁ сумма противоположных углов равна 180^○, а значит, он является вписанным, то есть точка H₁ лежит на окружности.

Докажем, что H₁B – диаметр. Так как треугольник ABC отображается в треугольник CAD, то _∠EAC = _∠ACB. Но из прямоугольного треугольника ACE имеем _∠EAC+_∠ACE = 90^○. Тогда _∠ACB+ _∠ACE = _∠H₁CB = 90^○. А так как вписанный прямой угол опирается на диаметр, то H₁B – это диаметр.

Теорема 6.8.9. Центр описанной около треугольника окружности служит ортоцентром треуголь- ника с вершинами в серединах сторон данного треугольника.

Рис. 121. Теорема 6.8.9.

Доказательство.

Рассмотрим треугольник ABC, в котором точки M,N,P – это середины сторон AB,AC,BC, а точка O – центр описанной окружности. Докажем, что O – ортоцентр треугольника MNP.

Так как центр описанной окружности лежит на серединных перпендикулярах к сторонам треуголь- ника, то, например,PO ⊥ BC. А так как MN средняя линия, и, следовательно, MN ∥ BC, то PO ⊥ MN. Таким образом PK – это высота треугольника MNP. Аналогично ML и NH – высоты треугольника MNP. Таким образом точка O является ортоцентром треугольника MNP.

Теорема 6.8.10. Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстоя- ние от центра описанной окружности до противоположной стороны.

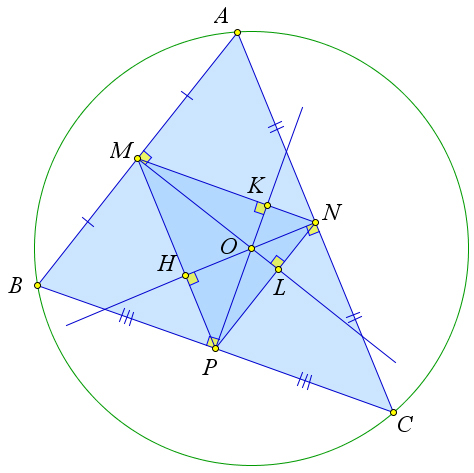
73

Доказательство.

Рассмотрим треугольник ABC, в котором точка H – это ортоцентр, а точка O – это центр описанной окружности. Докажем, что расстояние от точки O до стороны BA (обозначим его BD) вдвое меньше отрезка CH.

Основываясь на следствии 6.5.4.1, построим треугольник MNP, для которого треугольник ABC будет серединным. Тогда по следствию 6.5.4.2 точка H является центром окружности, описанной около _△MNP. Таким образом отрезок CH в треугольнике MNP соответствует отрезку OD в треугольнике ABC. А так как по следствию 6.5.4.1 эти треугольники подобны с коэффициентом 2, получаем, что CH = 2OD.

􏰁􏰁→ 􏰁→ 􏰁→ 􏰁→ Теорема 6.8.11. Если O - центр описанной окружности _△ABC, то OH = OA + OB + OC.

Рис. 122. Теорема 6.8.11.

Доказательство.

Рассмотрим треугольник ABC, в котором точка O – центр описанной окружности, точка H – ортоцентр, D – середина стороны AC, BB₁ – высота.

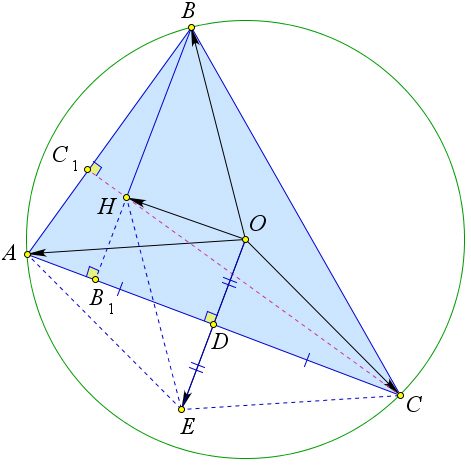
Отложим на серединном перпендикуляре OD точку E так, чтобы DE = OD. Тогда AOCE – парал- 􏰁→ 􏰁→ 􏰁→

лелограмм (так как диагонали точкой пересечения делятся пополам), а, следовательно, OA+OC = OE.

Кроме того прямые BH и OE перпендикулярны стороне BC, следовательно BH ∥ OE. Кроме того по

􏰁→ 􏰁→ 􏰁􏰁→ теореме 6.8.10 BH = 2OD = OE. Следовательно, BOEH – параллелограмм, а значит OB + OE = OH.

􏰁→ 􏰁→ 􏰁→ 􏰁􏰁→ Таким образом OA + OB + OC = OH.

Теорема 6.8.12. OH = ^√9R² −(a² +b² +c²) , где R- радиус описанной окружности; a,b,c – длины сторон треугольника.

Рис. 123. Теорема 6.8.12.

Доказательство.

Рассмотрим треугольник ABC, около которого описана окружность с центром O. Центральный угол BOC и вписанный угол BAC опираются на дугу BC, поэтому _∠BAC = 2 ⋅ _∠BOC. Кроме того по обобщённой теореме синусов верны соотношения a = 2R sin A, b = 2R sin B, c = 2R sin γ. Учитывая эти соотношения, а так же теорему 6.8.11, получаем

􏰁􏰁→ 􏰁→ 􏰁→ 􏰁→ 􏰁→􏰁→ 􏰁→􏰁→ 􏰁→􏰁→ OH² = OH² = (OA + OB + OC)² = OA² + OB² + OC² + 2OA ⋅ OB + 2OA ⋅ OC + 2OB ⋅ OC =

3R² + 2R² cos 2A + 2R² cos 2B + 2R² cos 2C = 3R² + 2R²(1 − 2 sin² A) + 2R²(1 − 2 sin² B) + 2R²(1 − 2 sin² C) = 9R² −(4R²sin²A+4R²sin²B+4R²sin²C)=9R² −(a² +b² +c²).

74