5.2 Косинус

Определение 5.2 (Общее определение).
1. Косинус острого угла равен отношению проекции к наклонной.
2. Косинус тупого угла равен косинусу смежного с ним угла, взятого с другим знаком. 3. Косинус прямого угла равен нулю.
4. Косинус развернутого угла равен минус единице.

Теорема 5.2.1 (корректность определения косинуса). Значение косинуса угла не зависит от того, какую длину наклонной выбрать.

Доказательство.

Первый способ. Следует из корректности определения синуса и теоремы Пифагора. Второй способ. Следует из подобия треугольников.

Теорема 5.2.2 (Свойства косинуса).
1. Косинус любого угла не больше 1 и не меньше −1.
2. cos(180^○ −α)=−cosα.
3. При возрастании угла от 0^○ до 180^○ косинус убывает от 1 до -1. 4. Косинус однозначно определяет угол.

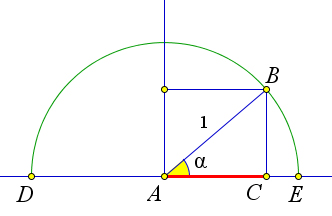
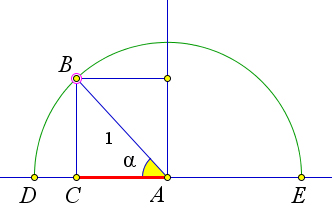
a) AC =cosα

b) AC =−cosα

Рис. 77. Теорема 5.2.2.

45

Доказательство.

Первое свойство следует из того, что проекция меньше наклонной.
Второе свойство следует из того, что углы 180^○ − α и α являются смежными.
Докажем третье свойство. Рассмотрим окружность единичного радиуса с центром в точке A и

диаметром DE (рис. 77). Пусть на прямой DE задана числовая ось с началом в точке A и единичным отрезком AE. Проведем радиус AB и получим угол _∠BAE некоторой величины α. Пусть точка C является проекцией точки B на прямую DE. Тогда cosα = AC при α ⩽ 90^○ (рис. 77 a) и cosα = −AC при α > 90^○ (рис. 77 b). Это означает, что cos α равен координате точки C на оси AE.

Когда α возрастает 0^○ до 180^○ (то есть, когда точка B пробегает полуокружность от точки E до точки D), точка C пробегает диаметр ED от точки E до точки D. При этом координата точки C, то есть cos α, убывает от 1 до −1.

Докажем четвертый пункт теоремы. Пусть cos α = cos β. Докажем, что тогда α = β. Действительно, возможно три случая:

1. α > β. Тогда по пункту 3 cos α < cos β. Значит, этот случай не имеет места. 2. α < β. Тогда по пункту 3 cos α > cos β. Значит, этот случай не имеет места. 3. Следовательно, остаётся только третья возможность: α = β.

Теорема 5.2.3 (Теорема косинусов). В каждом треугольнике квадрат любой его стороны равен сум- ме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Доказательство.

Первый способ.

a)

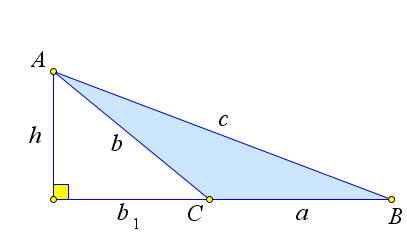
Рис. 78. Теорема 5.2.3.

Рассмотрим треугольник ABC со сторонами a,b и c. Докажем, что c² = a² +b² −2abcosC. Возможны три случая: 1) _∠C =90^○, 2) _∠C <90^○, 3) _∠C >90^○.

Первый случай. Пусть _∠C = 90^○. Тогда cosC = 0 и требуемое равенство обращается в теорему Пифагора для прямоугольного треугольника ABC.

Второй случай. Пусть _∠C < 90^○ (рис. 78 a). В треугольники ABC есть ещё хотя бы один острый угол. Пусть это будет угол B. Из вершины A проведем высоту AD. Так как углы B и C острые, точка D лежит на стороне BC. Отрезок CD = b₁ будет катетом в прямоугольном треугольнике ACD с гипотенузой AC = b и прилежащим острым углом C. Поэтому

b₁ =bcosC. (1)

По теореме Пифагора находим c² из другого прямоугольного треугольника ABD с катетами AD = h и

BD = a−b₁. Получаем c² = (a−b₁)² +h². Но h² = b² −b²₁ из треугольника ACD. Подставив это выражение

для h² в предыдущее равенство и заменив b по формуле (1), получим: c² = a² − 2ab + b² + b² − b² =

¹¹11

a² −2abcosC+b².
Третий случай. Пусть _∠C > 90^○ (рис. 78 b). Снова проведем высоту AD = h из вершины A. Теперь

ее основание – точка D лежит на продолжении стороны BC за точку C. Снова обозначим отрезок CD через b₁. В этом случае BD = a + b₁ и из прямоугольного треугольника ABD по теореме Пифагора

c² = h² + (a + b₁)². (2) 46

b)

По определению косинуса тупого угла cos C = − ^b1 . Поэтому b₁ = −b cos C . Наконец, из треугольника b

ACD снова получаем, что h² = b² − b². Подставляя это выражение для h² и выражение для b , то есть 11

b =−bcosC в формулу (2), снова получаем: c² =b² −b² +a² +2ab +b² =a² +b² −2abcosC. ¹1¹1

Рис. 79. Теорема 5.2.3.

Второй способ.

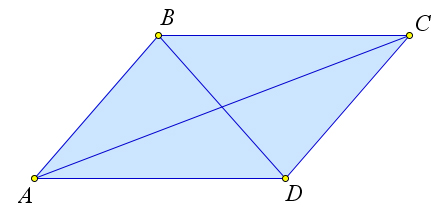
Теорема 5.2.4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сто- рон.

Рис. 80. Теорема 5.2.4.

Доказательство.

Рассмотрим параллелограмм ABCD (рис. 80). Докажем, что AC² + BD² = AB² + BC² + CD² + AD².

По теореме косинус для треугольника ABC имеем: AC² = AB² + BC² − 2 ⋅ AB ⋅ BC cos B. По теореме косинусов для треугольника BAD имеем: BD² = AB² + AD² − 2 ⋅ AB ⋅ AD cos A. Но так как ABCD – это параллелограмм, то _∠A = 180^○ − _∠B, BC = AD. Следовательно, cos A = − cos B и BD² = AB² + BC² + 2 ⋅ AB ⋅ BC cos B. Складывая это равенство с выражением для AC² получим: AC² + BD² = AB² +BC² +CD² +AD².

Теорема 5.2.5. Если m_c – медиана треугольника, проведенная к стороне c, то m_c = ^{1 √}2a² + 2b² − c² , 2

где a и b – остальные стороны треугольника.

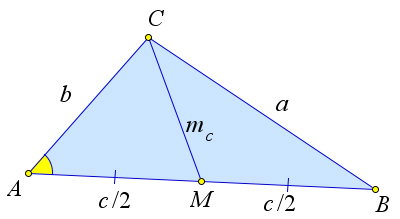
Рис. 81. Теорема 5.2.5.

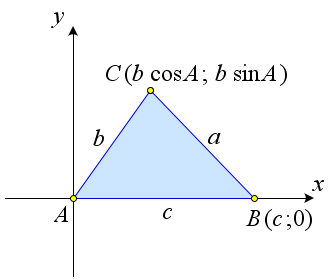
Рассмотрим треугольник ABC со сторонами a, b и c. Докажем, что a² = b² + c² − bc cos A. 􏰁→

Введем систему координат с началом в точке A так, чтобы Ox ⇈ AB, а точка C имела бы положительную ординату (рис. 79). Тогда точка B имеет координаты (c;0), а точка C имеет ко- ординаты (b cos A; b sin A). По формуле расстояния между двумя точками получаем: BC² = a² = (bcosA−c)² +b²sin²A=b²cos²A+b²sin²A−2bccosA+c² =b² +c² −2bccosA.

47

Доказательство.

Рассмотрим треугольник ABC со сторонами a,b,c и медианой CM = m (рис. 81). Докажем, что

m_c = ¹ 2

b² +c² −a²
_2bc . По теореме косинусов для

√

2a² +2b² −c².
По теореме косинусов для треугольника ABC имеем: cos A =

c

треугольникаACMимеем:m²=b²+(^c)2−2b^ccosA=b²+^c2 −^b2^+c2^−a2 =^4b2^+c2^−2b2^−2c2^+2a2 =

2a² +2b² −c²

√

22424

c
. Откуда после извлечения корня из обеих частей равенства и следует, что m_c =

1 2

4
2a² +2b² −c².

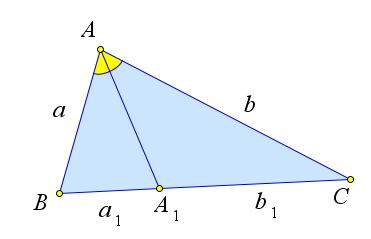
Теорема 5.2.6. Если AA₁ – биссектриса треугольника ABC, то AA₁ = ^√AB ⋅ AC − BA₁ ⋅ A₁C.

Рис. 82. Теорема 5.2.6.

Доказательство.

Рассмотрим треугольник ABC, в котором проведена биссектриса CK. Пусть AC = b, BC = a, AA

=

√

1

ab−a₁b₁.
Рассмотрим случай, когда a = b, то есть треугольник ABC – равнобедренный. Тогда CK – бис-

a₁,BA₁ =b₁,CA₁ =l (рис. 82). Докажем, что l=

сектриса и высота, и требуемая формула обращается в теорему Пифагора для треугольника ACK: l = ^√ b ² − b ²₁ .

Рассмотрим случай, когда a ≠ b. Обозначим половину угла C за α, и выразим cosα по теореме

a² +l² −a² b² +l² −b² косинусов двумя способам: из треугольников ACK и BCK. Получим cos α = ¹ = ¹ .

2al
Откуда a²b+l²b−a²b = b²a+l²a−b²a. Тогда l²(b−a) = ab(b−a)+a²b−b²a = ab(b−a)+a ⋅a b−b ⋅b a. По свойству

2bl биссектрисы ^a = ^a1 или ab₁ = ba₁. Следовательно, l²(b−a) = ab(b−a)+a₁ ⋅b₁a−b₁ ⋅a₁b = ab(b−a)−a₁b₁(b−a).

11111111

b b₁
И поскольку треугольник a≠b, то l² =ab−a₁b₁ или l=

5.3 Тангенс и котангенс

√

ab−a₁b₁.

Определение 5.3. Тангенсом угла называется отношение синуса угла к его косинусу. Определение 5.4. Котангенсом угла называется отношение косинуса угла к его синусу. Теорема 5.3.1 (Свойства тангенса).

1. При увеличении угла от 0^○ до 90^○ тангенс растет от 0 до бесконечности. 2. tg(180^○ −α)=−tgα.
3. Для острых углов значение тангенса определяет угол.

48

Доказательство.

Докажем первый пункт теоремы.

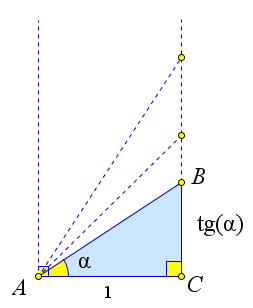
Рис. 83. Теорема 5.3.1.

Построим прямоугольный треугольник ABC, у которого AC = 1 и _∠A = α (рис. 83). Тогда другой его катет BC = tg α. Когда угол α возрастает от 0^○ до 90^○ катет BC, а значит и tg α, возрастает от 0 до бесконечности.

Докажем второй пункт теоремы.

tg(180^○ −α)= ^sin(180○ ^−α) = ^sinα =−tgα. cos(180^○ −α) −cosα

Докажем третий пункт теоремы.
Пусть углы α и β – острые. Докажем, что если tg α = tg β, то α = β. Действительно, возможно три

случая:
1. α > β. Тогда по пункту 1 tg α > tg β. Значит, этот случай не имеет места. 2. α < β. Тогда по пункту 1 tg α < tg β. Значит, этот случай не имеет места. 3. Следовательно, остаётся только третья возможность: α = β.