5 Начала тригонометрии

5.1 Синус

Определение 5.1 (Общее определение синуса).
1. Синус острого угла равен отношению перпендикуляра к наклонной. 2. Синус тупого угла равен синусу смежного острого угла.
3. Синус прямого угла равен единице.
4. Синус развернутого угла равен нулю.

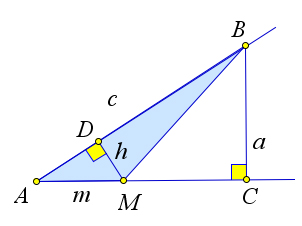
Теорема 5.1.1 (Корректность определения синуса). Пусть из точки B, лежащей на стороне p острого угла A, опущен перпендикуляр BC на сторону q этого угла. Тогда отношение перпенди- куляра BC к наклонной BA не зависит от выбора точки B.

41

Доказательство.

a)

b)

Рис. 71. Теорема 5.1.1.

Первый способ (не использует подобия).
На стороне q выберем любую точку M. Выразим площадь S треугольника ABM двумя способами.

С одной стороны, S = ¹ma, где a = BC,m = AM. C другой стороны, S = ¹ch, где h = MD – высота 22

треугольника ABM и c=BA (рис. 71 a). Поэтому ma=ch или ^a = ^h . cm

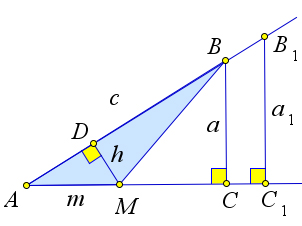
Если на стороне p взять другую точку B₁ и повторить проведенные рассуждения, то снова получим, что ^a1 = ^h , где a₁ =B₁C,c₁ =AB₁ (рис. 71 b). Поэтому ^a1 = ^a.

c₁ m c₁ c
Отношение перпендикуляра к наклонной не зависит от того, на какую сторону угла опущен пер-

пендикуляр. Действительно, пусть, как и раньше, M – точка на стороне q угла A и M D ⊥ p. Вернемся к равенству ^a = ^h . В правой части этого равенства стоит отношение перпендикуляра к наклонной,

cm

которое с выбором точки M не связано. Значит правая часть этого равенства от выбора точки M не зависит.

Второй способ (использует подобие). Если на стороне p взять точки B и B₁ и опустить из них

перпендикуляры BC и B₁C₁ к стороне q угла A, то треугольники ABC и AB₁C₁ будут подобны по

двум углам (рис. 71 b). Следовательно, ^BC = ^B1C1 . AB AB₁

Отношение перпендикуляра к наклонной не зависит от того, на какую сторону угла опущен перпен-

дикуляр. Действительно, пусть, как и раньше, M – точка на стороне q угла A и M D ⊥ p. Треугольники

ADM и ABC подобны по двум углам (_∠A – общий). Следовательно, ^MD = ^BC , а отношение, стоящее

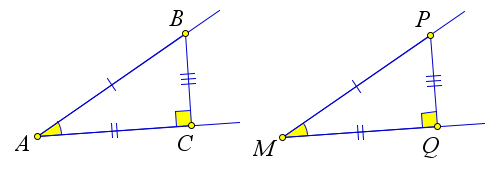
в правой части этого равенства не зависит от выбора точки M. Теорема 5.1.2. Синусы углов, имеющих равные величины, равны.

Рис. 72. Теорема 5.1.2.

Доказательство.

Возьмем два равных острых угла: _∠A и _∠M (рис. 72). Из некоторой точки B на стороне угла A опустим перпендикуляр BC на другую сторону угла A. Получим прямоугольный треугольник ABC. Отложим на сторонах угла M отрезки MP = AB и MQ = AC. Тогда _△MPQ = _△ABC по первому признаку равенства. Поэтому _∠Q = _∠C = 90^○. Итак PQ – перпендикуляр, опущенный из точки P одной стороны угла M на другую его сторону. Но тогда sin_∠A = ^BC = ^PQ = sin_∠M.

AB PM

Теорема 5.1.3 (Свойства синуса).
1^○ Синус каждого угла не больше единицы.
2^○ При возрастании угла от 0^○ до 90^○ его синус возрастает от 0 до 1. 3^○ При возрастании угла от 90^○ до 180^○ его синус убывает от 1 до 0. 4^○ sin(180^○ −α)=sinα.

AM AB

42

5^○ Величина острого угла определяется его синусом.

Доказательство.

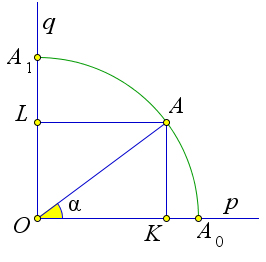
Рис. 73. Теорема 5.1.3.

Первый пункт следует из того, что перпендикуляр короче наклонной.

Докажем второй пункт теоремы. Возьмем прямой угол O со сторонами p и q (рис. 73). Из вершины O внутрь этого угла проведем единичный отрезок OA, образующий с лучом p острый угол α. Из точки A опустим перпендикуляры AK и AL на лучи p и q. Получим прямоугольник OKAL. Так как OA = 1, то AK = sin α. А поскольку OL = AK, то OL = sin α. Итак sin α равен длине проекции OL единичного отрезка OA на луч q. Когда угол α возрастает от 0^○ до 90^○, отрезок OA поворачивается вокруг точки O от положения OA₀ на луче p до положения OA₁ на луче q. Точка A пробегает четверть окружности. При этом точка L движется от точки O до точки A₁. Длина отрезка OL, то есть sinα возрастает от 0 до 1.

Докажем третий пункт теоремы. Когда тупой угол возрастает от 90^○ до 180^○, смежный ему острый угол убывает от 90^○ до 0^○ В этом случае по пункту 2 синус такого угла убывает от 1 до 0.

Докажем четвертый пункт теоремы. Пусть sin α = sin β. Докажем, что тогда α = β. Действительно, возможно три случая:

1. α > β. Тогда по пункту 2 sin α > sin β. Значит, этот случай не имеет места. 2. α < β. Тогда по пункту 2 sin α < sin β. Значит, этот случай не имеет места. 3. Следовательно, остаётся только третья возможность: α = β.

Теорема 5.1.4.

1. Площадь треугольника равна половине произведения двух его сторон на синус угла, заключен- ного между ними.

2. Площадь параллелограмма равна произведению двух его смежных сторон на синус угла, заклю- ченного между ними.

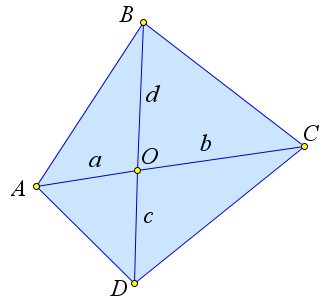
3. Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.

a)

b)
Рис. 74. Теорема 5.1.4.

43

c)

Доказательство.

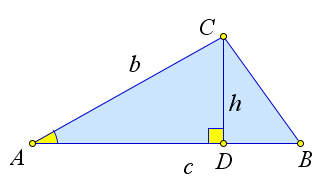
Докажем первый пункт теоремы. Пусть в треугольнике ABC известны стороны b, c и угол A между ними (рис. 74 a). Докажем, что S_ABC = ¹bcsinA. Действительно, проведем высоту h = CD из вершины

2

C. Тогда sinA = ^h. Поэтому h = bsinA. Тогда S_ABC = ¹ch = ¹bcsinA. ^b22

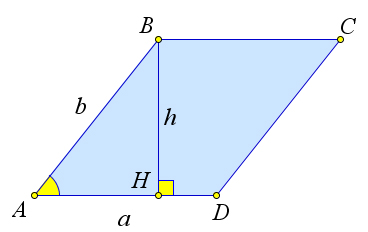
Докажем второй пункт теоремы. Пусть в параллелограмме ABCD известны стороны a,b и угол A

между ними (рис. 74 b). Докажем, что S_ABCD = ab sin A. Действительно, проведем высоту h = BH из

вершины B. Тогда sinA = ^h. Поэтому h = bsinA. Тогда S_ABCD = ah = absinA. b

Докажем третий пункт теоремы. Рассмотрим произвольный выпуклый четырехугольник. Пусть его диагонали пересекаются в точке O. Обозначим a = AO, b = CO, c = DO, d = BO (рис. 74 c). Кроме того, _∠AOB = _∠COD, а углы _∠BOC и _∠AOD являются смежными к ним. Следовательно, синусы углов _∠AOB, _∠BOC, _∠COD и _∠AOD равны. Обозначим sin _∠AOB = sin α. Тогда S_ABCD = S_ABO + S_BOC +

S_COD+S_AOD = ¹sinα(ad+db+bc+ca)= ¹sinα(d(a+b)+c(b+a))= ¹sinα(a+b)(c+d)= ¹sinα⋅AC⋅BD. 2222

Теорема 5.1.5. В любом выпуклом четырехугольнике ABCD выполняется соотношение S_△AOB ⋅ ^S_△COD ^=S_△BOC ^⋅S_△AOD^.

Рис. 75. Теорема 5.1.5.

Доказательство.

Рассмотрим произвольный выпуклый четырехугольник. Пусть его диагонали пересекаются в точке O. Обозначим a = AO,b = CO,c = DO,d = BO (рис. 75). Кроме того, _∠AOB = _∠COD, а углы _∠BOC и _∠AOD являются смежными к ним. Следовательно, синусы углов _∠AOB,_∠BOC,_∠COD и _∠AOD

равны. Обозначим sin_∠AOB = sinα. Тогда S_ABO ⋅S_COD = ¹ sinα⋅ad⋅ ¹ sinα⋅bc = ¹ sinα⋅db⋅ ¹ sinα⋅ac = S_BOC ⋅S_AOD. ^{2 2 2 2}

Следствие 5.1.5.1. В произвольной трапеции площади треугольников, на которые трапецию делят диагонали, удовлетворяют соотношению S² = S₁ ⋅ S₂.

Доказательство.

Рассмотрим трапецию ABCD в которой диагонали AC и BD пересекаются в точке O. По теореме 2.2.9 S_AOB = S_COD = S. Тогда введя обозначения S₁ = S_BOC, S₂ = S_AOD и учитывая теорему 5.1.5 получим S² = S₁ ⋅ S₂.

Теорема 5.1.6 (Теорема синусов). Синусы углов треугольника пропорциональны противолежащим сторонам.

Доказательство.

Пусть CD – это высота треугольника ABC, проведенная из вершины C. Тогда из прямоугольных треугольников ACD и BCD получим: CD = b sin A = a sin B, то есть ^a = ^b . Аналогично получим,

что ^a = ^c .Тогда ^a = ^b = ^c . sinA sinC sinA sinB sinC

Теорема 5.1.7. Биссектриса треугольника вычисляется по формуле l = ^{ab sin 2α} . (a+b) sin α

sin A sin B

44

Доказательство.

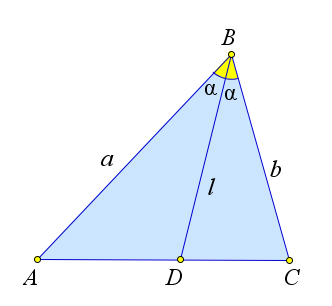
Рис. 76. Теорема 5.1.7.

Рассмотрим треугольник ABC, в котором проведена биссектриса BD, _∠ABC = 2α. Тогда _∠ABD = _∠BDC = α.

Треугольники ABC и ABD имеют общую высоту, проведенную из вершины B. Следовательно, S_ABC ∶ S_ABD = AC ∶ AD = ^a+b. Последнее равенство следует из теоремы 3.3.2. Кроме того, ^SABC =

a
1 ^{ab sin 2α} = . Сравнивая полученные равенства для отношений площадей, получим:

^SABD a+b bsin2α

₂ bsin2α ¹ al sin α l sin α

a

=

l sin α

.

2

Откудаl= ^absin2α . (a+b) sin α