
Примерные билеты к экзамену по геометрии в 9-5 классе. 2011-2012 учебный год.
1. Признаки равенства треугольников. Определения 1.1, 1.2 , аксиомы 1, 2 , теоремы 1.1.1,1.1.2,1.1.3 .
2. Равнобедренный треугольник. Теоремы 1.2.1,1.2.2 .
3. Параллельные прямые. Теорема о сумме углов треугольника и следствия из неё. Теоремы 1.3.4,1.3.5, 1.4.1 , следствие 1.4.1.1 .
4. Неравенство треугольника. Теоремы 1.5.2,1.5.1, следствия 1.5.1.1, 1.5.1.2 .
5. Прямоугольный треугольник. Теоремы 1.6.1,1.6.2, 1.6.3, 1.6.4, 1.6.5, 1.6.6 .
6. Параллелограмм. Теоремы 2.2.1,2.2.2, определение 2.1 .
7. Прямоугольник, ромб, квадрат. Теоремы 2.2.3 - 2.2.8, определение 2.2, 2.3, 2.4 .
8. Трапеция. Теоремы 2.2.10, 2.2.11, определение 2.5, 2.6 .
9. Средняя линия треугольника. Параллелограмм Вариньона. Теоремы 2.3.1, 2.3.2, 2.3.3 определение 2.7 .
10. Средняя линия трапеции. Теорема Фалеса. Теоремы 2.3.5, 2.3.6, 2.3.4 определение 2.8 .
11. Площади различных многоугольников. Теоремы 3.2.1-3.2.6 определение 3.1 .
12. Отношение площадей треугольников с равными элементами. Теорема 3.3.1 .
13. Теорема Пифагора. Обратная теорема Пифагора. Теоремы 3.4.1, 3.4.2 .
14. Формула Герона. Теорема 3.4.3 .
15. Признаки подобия треугольников. Теоремы 4.1.5-4.1.4 , Определения 4.1, 4.2 .
16. Пропорциональные отрезки в прямоугольном треугольнике. Теорема 4.2.3 .
17. Отношение площадей подобных треугольников. Площадь параллелограмма Вариньона. 1
Теоремы 4.1.5, 4.2.4 .
Теорема Чевы. Теорема 4.2.8 .
Теорема Менелая в скалярной формулировке. Теорема 4.2.9 .
Общее определение синуса. Формулы площадей различных фигур через синус. Теоремы 5.1.3, 5.1.4 . Определение 5.1 .
Теорема синусов. Свойство биссектрисы треугольника. Теоремы 5.1.6, 3.3.2.
Общее определение косинуса. Теорема косинусов. Теоремы 5.2.2, 5.2.3 . Определение 5.2 .
Формула для медианы треугольника. Теорема 5.2.5 .
Формула для биссектрисы треугольника. Теорема 5.2.6 .
Тригонометрические функции в прямоугольном треугольнике. Основные формулы тригономет- рии. Значения тригонометрических функций стандартных углов. Теоремы 5.4.1, 5.4.2 . Определения 5.5-5.8 .
Окружность. Взаимное расположение прямой и окружности. Характеристическое свойства каса- тельной к окружности. Теоремы 6.1.1, 6.1.2 . Определение 6.1 .
Дополнительные свойства касательной к окружности. Свойства хорд окружности. Теоремы 6.1.3, 6.1.4 .
Центральный и вписанный угол. Углы между различными элементами в окружности. Теоремы 6.3.1, 6.3.2 . Следствия 6.3.1.1, 6.3.1.2 . Определения 6.4-6.6 .
Пропорциональные отрезки в круге. Теорема о степени точки. Теоремы 6.4.1-6.4.4 . Определение 6.7 .
Центроид и ортоцентр. Свойство центроида. Теоремы 4.2.1, 6.5.4 . Определения 6.10, 6.11 .
Существование и единственность окружности вписанной в треугольник и описанной около тре- угольника. Теоремы 6.5.1, 6.5.3 . Следствия 6.5.2-6.5.2.2, 6.5.3.1-6.5.3.3 . Определения 2.2.2-6.10 .
Обобщенная теорема синусов. Формула для радиуса окружности, описанной около треугольника. Формула для радиуса окружности, вписанной в треугольник. Теоремы 6.6.4, 6.6.3 . Следствие 6.6.3.1 .
Характеристическое свойство вписанного четырёхугольника. Необходимое и достаточное условие существования окружности, описанной около трапеции. Теоремы 6.6.2 . Следствие 6.6.2.1 . 2
Характеристическое свойство описанного четырёхугольника. Теорема 6.6.1 .
Формулы для радиусов вписанной и описанной окружности для прямоугольного треугольника. Теорема об отношении, в котором инцентр разбивает биссектрису треугольника. Формула для вычисления отрезков, образованных вершинами треугольника и точками касания его вписанной окружности. Теоремы 6.6.6, 6.6.8, ??, 6.6.7 .
Свойства ортоцентра треугольника. Теоремы 6.8.1, 6.8.7, 6.8.6, ?? .
Правильные многоугольники. Теоремы 7.0.13-7.0.17 . Следствие 7.0.13.1 Определение 7.1
Длина окружности. Площадь круга. Теоремы 8.0.18-8.0.21 . Следствие 8.3, 8.0.21.1 .
Определение вектора. Определение линейных операций с векторами. Характеристическое свой- ство коллинеарных векторов. Теоремы 9.1.6-9.2.3, 9.3.4, 9.2.7 . Следствие определения 9.16 . Определения 9.1-9.16 .
Координаты вектора. Простейшие задачи в координатах. Теорема α − β . Теоремы 9.2.8, 9.3.3, 9.3.4-9.3.8. Определение 9.18, 9.19.
Скалярное умножение векторов. Теоремы 9.4.1-9.4.4 . Определения 9.20-9.22 .
Уравнения прямой. Теоремы 10.1.1, 10.1.2 .
Формула расстояния от точки до прямой. Теорема 10.1.4 .
Уравнение окружности. Парабола. Теоремы 10.2.1, 10.2.2 . Теорема 10.2.4 – только формулировка. Определение 10.1 .
Эллипс. Теоремы 10.2.5, 10.2.3 . Теорема 10.2.7 – только формулировка. Определение 10.2 .
Гипербола. Теоремы 10.2.8, 10.2.4 . Теорема 10.2.9 – только формулировка. Определение 10.3 .
Движения. Виды движений. Гомотетия. Преобразования в координатах. Теоремы 11.2.1 (только формулировка), 11.3.3, 11.3.4, 11.3.9, 11.3.12, 11.5.1 . Определения 11.5-11.10, 11.14 .
3
Содержание
1 Треугольники 6
1.1 Признакиравенстватреугольников.................................. 6
1.2 Равнобедренныйтреугольник ..................................... 8
1.3 Параллельныепрямые.......................................... 9
1.4 Теоремаосуммеугловтреугольникаиследствияизнеё . . . . . . . . . . . . . . . . . . . . 12
1.5 Неравенствотреугольника ....................................... 13
1.6 Прямоугольныйтреугольник...................................... 14 1.6.1 Прямоугольныйтреугольник ................................. 14 1.6.2 Прямоугольныйтреугольниксугломв30○ ........................ 16
2 Многоугольники. Четырехугольники 17
2.1 Многоуольники .............................................. 17
2.2 Четырехугольники ............................................ 19 2.2.1 Параллелограмм ......................................... 19 2.2.2 Прямоугольник.......................................... 20 2.2.3 Ромб................................................. 21 2.2.4 Квадрат .............................................. 22 2.2.5 Трапеция.............................................. 22
2.3 Средняялиниятреугольникаитрапеции.ТеоремаФалеса . . . . . . . . . . . . . . . . . . . 25
3 Площадь 29
3.1 Понятиеплощади............................................. 29
3.2 Площадиразличныхмногоугольников................................ 29
3.3 Отношениеплощадейтреугольниковсравнымиэлементами . . . . . . . . . . . . . . . . . . 31
3.4 ТеоремаПифагора ............................................ 33
4 Подобие треугольников 34 4.1 Признакиподобиятреугольников................................... 34 4.2 Применениеподобия ........................................... 36
5 Начала тригонометрии 41
5.1 Синус .................................................... 41
5.2 Косинус................................................... 45
5.3 Тангенсикотангенс ........................................... 48
5.4 Тригонометрические функции в прямоугольном треугольнике . . . . . . . . . . . . . . . . . 49
6 Окружность 51 6.1 Касательныеихорды .......................................... 51 6.2 Двеокружности.............................................. 53 6.3 Углывокружности............................................ 53 6.4 Пропорциональныеотрезкивкруге ................................. 56 6.5 Четырезамечательныеточкитреугольника ............................ 57 6.6 Вписаннаяиописаннаяокружности ................................. 61 6.7 Вневписанныеокружности ....................................... 66 6.8 Ортоцентр ................................................. 69
7 Правильные многоугольники 75
8 Длина окружности. Площадь круга 78
9 Векторы 80 9.1 Определениевектора........................................... 80 9.2 Линейныеоперациисвекторами ................................... 83 9.3 Координатывекторов .......................................... 88 9.4 Скалярноеумножениевекторов .................................... 91
4
10 Метод координат. Уравнение линий на плоскости 92
10.1Уравнениепрямой ............................................ 92 10.2Кривыевторогопорядка ........................................ 95 10.2.1 Окружность............................................ 95 10.2.2 Парабола.............................................. 95 10.2.3Эллипс............................................... 97 10.2.4 Гипербола ............................................. 99
11 Преобразования плоскости 102
11.1Основныеопределения.......................................... 102 11.2Движения.................................................. 103 11.3Видыдвижений.............................................. 104
11.3.1 Параллельныйперенос ..................................... 104 11.3.2 Осеваясимметрия ........................................ 105 11.3.3 Центральнаясимметрия .................................... 106 11.3.4 Поворот .............................................. 107
11.4Классификациядвижений ....................................... 107 11.5Гомотетия.................................................. 108
5
1 Треугольники
1.1 Признаки равенства треугольников
Определение 1.1. Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.
Определение 1.2. Треугольники называются равными, если их можно совместить наложением. Замечание. Это определение является частным случаем определения 11.6.
Аксиома 1. На любом луче от его начала можно отложить отрезок, равный данному, и при том только один.
Аксиома 2. От любого луча в заданную полуплоскость можно отложить угол, равный данному неразвернутому, и при том только один.
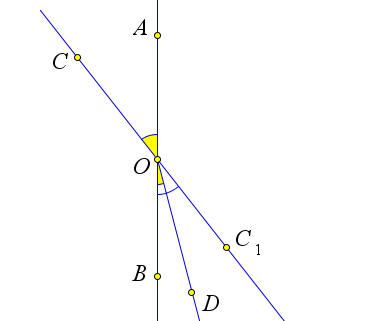
Следствие 2.1. Пусть на прямой AB точка O лежит между точками A и B. Если от лучей OA и OB в разные полуплоскости отложить лучи OC и OD соответственно так, чтобы ∠COA = ∠DOB, то точки C,O и D лежат на одной прямой (рис. 1).
Рис. 1. Следствие 2.1.
Доказательство.
Если предположить противное и продолжить луч CO за точку O, получив луч OC1, то получится, ∠COA = ∠BOC1, как вертикальные, и от луча OB отложены два равных угла ∠DOB и ∠COC1, что противоречит аксиоме 2 (рис. 1).
Аксиома 3. Через любые две точки проходит прямая, и при том только одна.
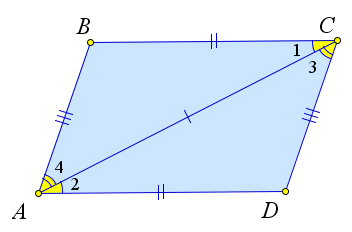
Теорема 1.1.1 (Первый признак равенства треугольников). Если две стороны и угол между ними од- ного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
![]()
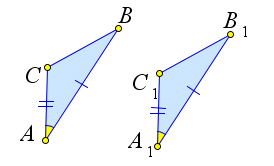
⎧⎪ AB = A1B1, △ABC, △A1B1C1 ∶ ⎨⎪ AC = A1C1,
⎪⎩ ∠ A = ∠ A 1 ,
Доказательство.
Рассмотрим треугольники ABC и A1B1C1, у которых AB = A1B1, AC = A1C1, ∠A = ∠A1. Докажем, что △ABC = △A1B1C1.
Так как ∠A = ∠A1, то согласно аксиоме 2 треугольник ABC можно наложить на треугольник A1B1C1 так, что вершина A совместиться с вершиной A1, а стороны AB и AC наложатся соответ- ственно на лучи A1B1 и A1C1. В силу аксиомы 1, так как AB = A1B1 и AC = A1C1, то стороны AB
⇒ △ABC = △A1B1C1.
6
Рис. 2. Теорема 1.1.1.
и A1B1, AC и A1C1 совместиться; в частности совместятся точки B и B1, C и C1. Следовательно, по аксиоме 3 совместятся и стороны BC и B1C1. Итак, треугольники ABC и A1B1C1 полностью совме- стились. Следовательно, согласно определению 1.2, они равны.
Теорема 1.1.2 (Второй признак равенства треугольников). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
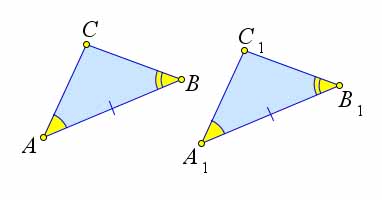
⎧⎪ AB = A1B1, △ABC, △A1B1C1 ∶ ⎨⎪ ∠A = ∠A1, ⇒ △ABC = △A1B1C1.
⎪⎩ ∠ B = ∠ B 1 ,
Доказательство.
Рассмотрим треугольники ABC и A1B1C1, у которых AB = A1B1, ∠A = ∠A1, ∠B = ∠B1. Докажем, что △ABC = △A1B1C1. Наложим треугольник ABC на треугольник A1B1C1 так, чтобы вершина A совместилась с вершиной A, сторона AB – с равной ей стороной A1B1, а вершины C и C1 оказались по одну сторону от прямой A1B1.
Так как ∠A = ∠A1 и ∠B = ∠B1, то по сторона AC наложится на луч A1C1, а сторона BC – на луч B1C1. Поэтому вершина C – общая точка сторон AC и BC – окажется как лежащей на луче A1C1, так и на луче B1C1 и, следовательно, совместиться с общей точкой этих лучей – вершиной C1. Значит, совместятся стороны AC и A1C1, BC и B1C1. Итак треугольники ABC и A1B1C1 полностью совместятся. Следовательно, они равны.
Теорема 1.1.3 (Третий признак равенства треугольников). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Замечание. Эту теорему можно доказать только после доказательства теоремы 1.2.1.
Рис. 3. Теорема 1.1.2.
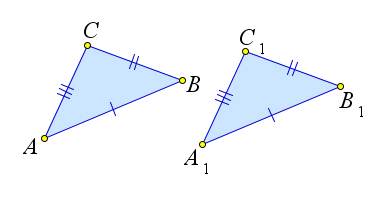
⎧⎪ AB = A1B1, △ABC, △A1B1C1 ∶ ⎨⎪ AC = A1C1, ⇒ △ABC = △A1B1C1.
⎪⎩ B C = B 1 C 1 ,
Доказательство.
Рассмотрим треугольники ABC и A1B1C1, у которых AB = A1B1, AC = A1C1, BC = B1C1. Докажем, что △ABC = △A1B1C1. Приложим треугольник ABC к треугольнику A1B1C1 так, чтобы вершина A совместилась с вершиной A1, вершина B – C вершиной B1, а вершины C и C1 оказались по разные стороны от прямой A1B1.
Возможны три случая: 1) луч C1C проходит внутри угла A1C1B1; 2) луч C1C совпадает с одной из сторон этого угла; 3) луч C1C проходит вне угла A1C1B1.
7
Рис. 4. Теорема 1.1.3.
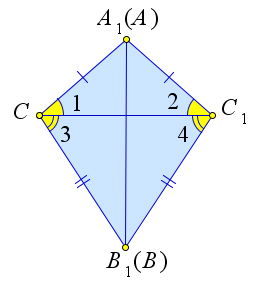
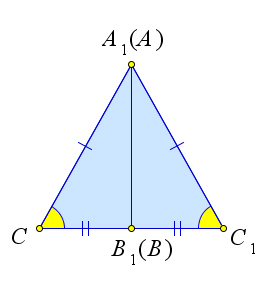
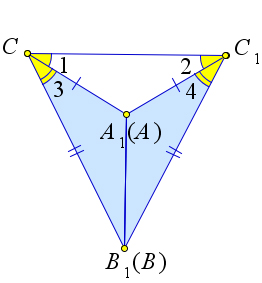
Случай 1. Случай 2. Случай 3. Рис. 5. Теорема 1.1.3.
Рассмотрим первый случай. По условию теоремы AB = A1B1, AC = A1C1, BC = B1C1, следователь- но, треугольники A1C1C и B1C1C – равнобедренные. По теореме (1.2.1) ∠1 = ∠2,∠3 = ∠4, поэтому ∠A1CB1 = ∠A1C1B1. Итак, AC = A1C1,BC = B1C1,∠C = ∠C1. Следовательно, треугольники ABC и A1B1C1 равны по первому признаку равенства треугольников (теорема 1.1.1).
Рассмотрим второй случай. Пусть луч C1C совпадает со стороной C1B угла A1C1B1. Тогда, так как AC = A1C1, то треугольник A1C1 равнобедренный, и ,следовательно, ∠C = ∠C1. Тогда треугольники A1BC1 и ABC равны по первому признаку равенства треугольников.
Третий случай доказывается аналогично первому.
1.2 Равнобедренный треугольник
Теорема 1.2.1 (Свойства равнобедренного треугольника).
1○. Углы при основании равнобедренного треугольника равны.
2○. Медиана, высота и биссектриса равнобедренного треугольника, проведенные к основанию, сов- падают.
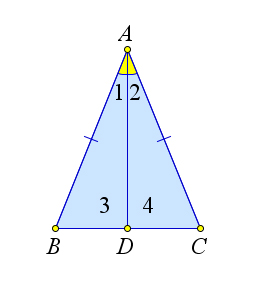
AB=AC⇒{ ∠B=∠C, AD − медиана, биссектриса и высота.
Доказательство.
Рис. 6. Теорема 1.2.1.
Рассмотрим равнобедренный треугольник ABC с основанием BC. Пусть AD – биссектриса этого треугольника. Треугольники ABD и ACD равны по первому признаку равенства треугольников (AB = AC, AD – общая, ∠1 = ∠2). Следовательно, ∠B = ∠C. Кроме того, ∠3 = ∠4, а поскольку они смежные, то каждый из них является прямым, то есть AD – высота. Из равенства этих треугольников следует, что BD = DC, следовательно AD – не только биссектриса и высота, но и медиана.
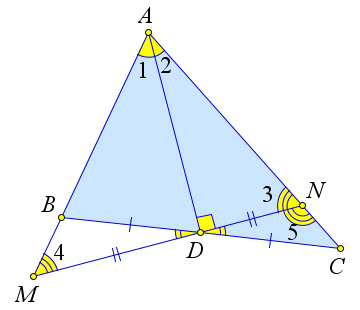
Теорема 1.2.2 (Признаки равнобедренного треугольника). 1. Если два угла треугольника равны, то треугольник равнобедренный. 2. Если медиана треугольника является его высотой, то треугольник равнобедренный. 3. Если биссектриса треугольника является его высотой, то треугольник равнобедренный. 4. Если медиана треугольника является его биссектрисой, то треугольник равнобедренный.
Замечание. Пункт 4 можно доказать только после доказательства теоремы 1.3.4. 8
Доказательство.
Рис. 7. Теорема 1.2.2.
Рассмотрим треугольник ABC (рис. 7). Докажем, что если ∠B = ∠C, то AB = AC. Первый способ. Поскольку ∠B и ∠C острые (иначе сумма углов треугольника ABC была бы больше 180○), то
высота, проведенная из вершины A падает на сторону BC. Так как сумма углов треугольника равна 180○, то ∠1 = 180○ −90○ −∠B = 180○ −90○ −∠C = ∠2. Следовательно, треугольники ABD и ACD равны по второму признаку равенства треугольников (∠1 = ∠2,∠3 = ∠4,AD– общая сторона). Тогда AB = AC, то есть треугольник равнобедренный.
Второй способ.
Если предположить, что одна из указанных сторон больше другой, то по теореме 1.5.1 угол, лежа- щий против нее, будет больше угла, лежащего против другой стороны, а это противоречит условию (тому, что данные углы равны). Итак AB = AC.
Докажем теперь, что если AD – медиана и высота, то треугольник равнобедренный. Действитель- но, так как BD = DC,∠3 = ∠4 = 90○, a AD – общая сторона, то треугольники ABD и ACD равны по первому признаку равенства треугольников. Следовательно, AB = AC, то есть треугольник равнобед- ренный.
Докажем, что если AD – биссектриса и высота для △AB, то треугольник равнобедренный. Дей- ствительно, так как ∠1 = ∠2,∠3 = ∠4 = 90○, a AD – общая сторона, то треугольники ABD и ACD равны по второму признаку равенства треугольников. Следовательно, AB = AC, то есть треугольник равнобедренный.
Рис. 8. Теорема 1.2.2.
Докажем, что если AD – медиана и биссектриса, то треугольник равнобедренный (рис. 8). Предпо- ложим противное – треугольник ABC неравнобедренный, и, следовательно, AD не высота. Проведем через точку D прямую l перпендикулярно AD. Обозначим точки пересечения прямой l с прямыми AB и AC как M и N соответственно. Треугольник AMN – равнобедренный, так как AD – биссек- триса и высота этого треугольника. Тогда AD – медиана треугольника AMN, то есть MD = ND. Тогда треугольники BMD и CND равны по первому признаку (∠BDM = ∠CDN как вертикаль- ные, BD = DC,MD = ND). Тогда ∠4 = ∠5, и следовательно прямые AB и AC параллельны, что невозможно.
1.3 Параллельные прямые
Определение 1.3. Две прямые на плоскости называются параллельными, если они не имеют общих точек.
9
Аксиома 4. Через данную точку можно провести не более одной прямой, параллельной данной. Утверждение 1.3.1. Если прямая пересекает одну из двух данных параллельных прямых, то она
пересекает и вторую.
Доказательство.
Пусть прямые a и b параллельны, и прямая пересекает прямую a в точке M. Если предполо- жить, что прямая c не пересекает прямую b, то получится, что через точку M проходит две прямые, параллельные прямой a, что противоречит аксиоме 4.
Утверждение 1.3.2. Если две прямые параллельны третьей прямой, то они параллельны.
Доказательство.
Пусть прямые a и b параллельны прямой c. Если предположить, что прямые a и b пересекаются в точке M, то получится, что через точку M проходит две прямые, параллельные прямой c, что противоречит аксиоме 4.
Лемма 1.3.3. Если две прямые перпендикулярны данной прямой, то они параллельны.
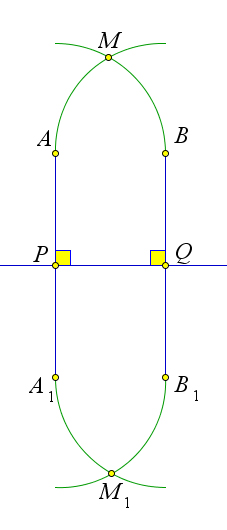
a)
Рис. 9. Лемма 1.3.3.
Доказательство. Первый способ. Пусть a⊥AB,b⊥AB. Докажем, что a∥b (рис. 9 а). Предположим противное: a∩b=M. Выберем
на прямой a точку M1 так, чтобы AM = AM1. Тогда △ABM = △ABM1 по первому признаку равенства треугольников (AM = AM1, AB – общая, ∠1 = ∠MAB = 90○). Но тогда ∠2 = ∠ABM1 = 90○, следо- вательно, (∠2 + ∠ABM1) = 180○, то есть точки M, B, M1 лежат на одной прямой, а это противоречит аксиоме 3, так как прямые BM и a пересекаются в двух различных точках M и M1.
Второй способ.
Рассмотрим прямые AA1 и BB1 перпендикулярные прямой PQ (рис. 9 b). Мысленно перегнем рисунок по прямой PQ. Так как AA1 ⊥ PQ, то луч PA наложится на луч PA1. Аналогично, луч QB наложится на луч QB1. Поэтому, если предположить, что прямые AA1 и BB1 пересекаются в точке M, то эта точка наложится на некоторую точку M1, также лежащую на этих прямых, что противоречит аксиоме 3.
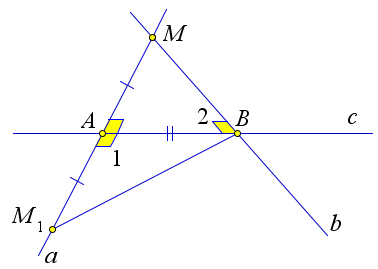
Теорема 1.3.4 (Признаки параллельности прямых).
1. Если при пересечении двух прямых третьей образуются равные внутренние накрест лежащие углы, то прямые параллельны.
b)
10
2. Если при пересечении двух прямых третьей образуются равные соответственные углы, то прямые параллельны.
3. Если при пересечении двух прямых третьей сумма односторонних углов равна 180○, то прямые параллельны.
Доказательство.
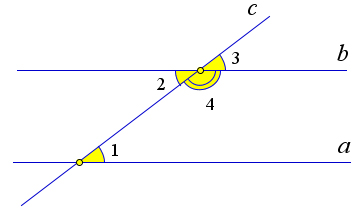
Докажем первый пункт теоремы.
a)
b)
Рис. 10. Теорема 1.3.4.
Пусть при пересечении прямых a и b секущей AB накрест лежащие углы равны: ∠1 = ∠2. Докажем, что тогда a ∥ b.
Если ∠1=∠2=90○. Тогда a∥b в силу леммы 1.3.3.
Рассмотрим случай, когда ∠1 = ∠2 ≠ 90○ (рис. 10 a). Проведем из точки O – середины отрезка AB – перпендикуляр OH к прямой a. От точки B на прямой b отложим отрезок BH1 равный отрезку AH. Тогда △AOH = △BOH1 по первому признаку равенства треугольников (AO = OB,AH = BH1,∠1 = ∠2). Следовательно, ∠3 = ∠4,∠H = ∠H1 = 90○. Из равенства ∠3 = ∠4 следует, что точки H,O и H1 лежат на одной прямой. Из равенства ∠H = ∠H1 = 90○ следует, что прямые a и b перпендикулярны к прямой HH1, и следовательно, параллельны по лемме 1.3.3.
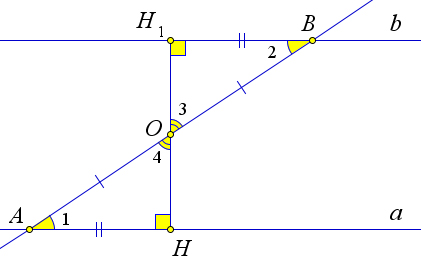
Докажем второй пункт.
Пусть при пересечении прямых a и b секущей c соответственные углы равны: ∠1 = ∠3 (рис. ?? b). Покажем, что a ∥ b. Действительно, ∠3 = ∠2, как вертикальные. Следовательно, ∠2 = ∠1, и прямые a и b параллельны по первому пункту теоремы.
Докажем третий пункт.
Пусть при пересечении прямых a и b секущей c ∠1 + ∠4 = 180○ (рис. ?? b). Покажем, что a ∥ b. Действительно, ∠2 = 180○ − ∠4 = ∠1. Следовательно, ∠2 = ∠1, и прямые a и b параллельны по первому пункту теоремы.
Теорема 1.3.5 (Свойства параллельности прямых). Если две параллельные прямые пересечены тре- тьей прямой, то образованные при этом накрест лежащие углы равны, соответственные углы рав- ны, и сумма односторонних углов равна 180○.
Рис. 11. Теорема 1.3.5.
Доказательство.
Пусть параллельные прямые a и b пересечены секущей MN. Покажем, что накрест лежащие углы, например ∠1 и ∠2, равны (рис. 11).
Предположим противное, то есть ∠1 ≠ ∠2. Отложим от луча MN угол ∠PMN, равный углу ∠2, так, чтобы ∠PMN и ∠2 были накрест лежащими при пересечении MP и b секущей MN. Тогда по
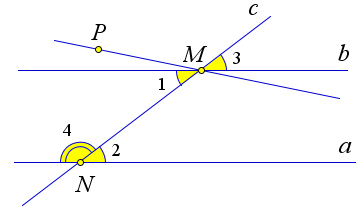
11
теореме 1.3.4 M P ∥ b. Тогда через точку M проходит две прямые (a и M P ) параллельные прямой b, а это противоречит аксиоме 4. Значит ∠1 = ∠2.
Так как ∠3 = ∠1 как вертикальные, то ∠3 = ∠2, то есть соответственные углы равны.
Так как ∠2 и ∠4 смежные, то 180○ = ∠2 + ∠4 = ∠1 + ∠4. То есть сумма односторонних углов равна 180○ .
Теорема 1.3.6. Острые углы с попарно параллельными сторонами равны. ?? 1.4 Теорема о сумме углов треугольника и следствия из неё
Теорема 1.4.1. Сумма внутренних углов треугольника равна 180○.
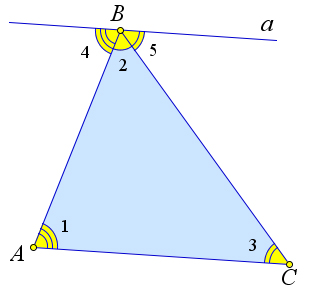
Рис. 12. Теорема 1.4.1.
Доказательство.
Рассмотрим произвольный треугольник ABC (рис. 12). Докажем, что ∠A + ∠B + ∠C.
Проведем через вершину B прямую a, параллельную стороне AC (рис 25). По теореме 1.3.5 ∠1 = ∠4,∠3=∠5, как накрест лежащие. Тогда ∠1+∠2+∠3=∠4+∠2+∠5=180○.
Следствие 1.4.1.1. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
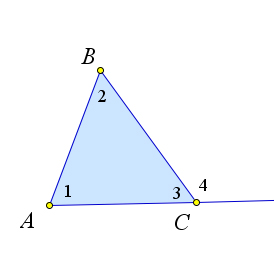
Рис. 13. Теорема 1.4.1.1.
Доказательство.
Углы ∠3 и ∠4 смежные (рис. 13), поэтому ∠4=180○ −∠3=180○ −(180○ −∠1−∠2)=∠1+∠2. Утверждение 1.4.2. Если биссектрисы углов B и C треугольника ABC пересекаются в точке M,
то ∠BMC = 90○ + ∠A/2. Утверждение 1.4.3. Биссектрисы смежных углов взаимно перпендикулярны.
Следствие 1.4.3.1. Биссектрисы внутренних односторонних углов при параллельных прямых и се- кущей перпендикулярны.
12
1.5 Неравенство треугольника
Теорема 1.5.1.
1. Против большей стороны треугольника лежит больший угол. 2. Против большего угла треугольника лежит большая сторона.
Доказательство.
Докажем первый пункт теоремы.
Рис. 14. Теорема 1.5.1.
Рассмотрим произвольный треугольник ABC. Пусть AB > AC. Докажем, что ∠C > ∠B. Отложим на стороне AB отрезок AD, равный стороне AC (рис. 14). Так как AD < AB, то точка D лежит между точками A и B. Следовательно, угол ∠1 является частью угла C и, значит, ∠C < ∠1. Угол ∠2 – внешний угол треугольника BDC, поэтому ∠2 > ∠B. Углы ∠1 и ∠2 равны, как углы при основании равнобедренного треугольника ADC. Таким образом, ∠C > ∠1 = ∠2 > ∠B.
Докажем второй пункт теоремы. Пусть в треугольнике ABC ∠C > ∠B. Докажем, что AB > AC. Предположим противное. Тогда либо AB = AC, либо AB < AC. В первом случае треугольник ABC
– равнобедренный и, значит, ∠C = ∠B. Во втором случае ∠B > ∠C (против большей стороны лежит больший угол). И то и другое противоречит условию ∠C > ∠B. Поэтому предположение неверно, и, следовательно, AB > AC.
Следствие 1.5.1.1. Гипотенуза прямоугольного треугольника больше катета. Следствие 1.5.1.2. Если из одной точки проведены к прямой перпендикуляр и наклонные, то пер-
пендикуляр короче наклонных, а большей наклонной соответствует большая проекция и наоборот.
Теорема 1.5.2 (Неравенство треугольника). Каждая сторона треугольника меньше суммы двух других сторон.
Рис. 15. Теорема 1.5.2.
Доказательство.
Рассмотрим треугольник ABC и докажем, что AB < AC + CB (рис. 15). Первый способ. Отложим на продолжении стороны AC отрезок CD, равный стороне CB (рис. 15). В равнобедрен-
ном треугольнике BCD ∠1 = ∠2, а в треугольнике ABD ∠ABD > ∠1 и, значит, ∠ABD > ∠2. Тогда по теореме 1.5.1 AB < AD = AC + CD = AC + CB.
13
Второй способ. √ √
По теореме косинусов AB = AC2 +CB2 −2⋅AB⋅AC⋅cosCˆ < AC2 +CB2 +2⋅AB⋅AC = ∣AC + CB∣ < ∣AC∣+∣CB∣ = AC +CB. Здесь в первом неравенстве использовали то, что cos Cˆ ≥ −1, а в последнем неравенстве использовали алгебраическое свойства модуля: ∣a + b∣ < ∣a∣ + ∣b∣.
1.6 Прямоугольный треугольник
1.6.1 Прямоугольный треугольник Теорема 1.6.1 (Признаки равенства прямоугольных треугольников).
![]()
![]()
1. По двум катетам. 2. По гипотенузе и острому углу. 3. По катету и острому углу. 4. По катету и гипотенузе.

Доказательство.
Рис. 16. Теорема 1.6.1.
Первый пункт теоремы верен, так как между катетами таких треугольников будут заключены равные между собой прямые углы, и треугольники будут равны по первому признаку равенства.
Второй и третий пункты теоремы верны, так как если острый угол одного прямоугольного тре- угольника равен острому углу другого прямоугольного треугольника, то их вторые острые углы тоже будут равны в силу теоремы 1.4.1. Тогда треугольники будут равны по второму признаку равенства.
Докажем четвертый пункт теоремы. Первый способ. Рассмотрим треугольники ABC и A1B1C1, у которых ∠C = ∠C1 = 90○, AB = A1B1, BC = B1C1 (рис.
16). Докажем, что △ABC = △A1B1C1. Так как ∠C = ∠C1, то треугольник ABC можно наложить на треугольник A1B1C1 так, что вер-
шина C совместиться с вершиной C1, а стороны CA и CB наложатся на лучи C1A и C1B. Поскольку CB = C1B1, то вершина B наложится на вершину B1. Докажем, что вершина A наложится на вер- шину A1. Действительно, если предположить, что точка A совместиться с некоторой точкой A2 луча C1A1, то получится, что треугольник A1B1A2 – равнобедренный, и, следовательно, ∠A1 = ∠A2. Но это невозможно, так как ∠A2 – острый (как угол прямоугольного треугольника B1C1A2), а ∠A1 – тупой ( как смежный с острым углом ∠C1A1B1).
Второй способ. Рассмотрим треугольники ABC и A1B1C1, у которых ∠C = ∠C1 = 90○, AB = A1B1, BC = B1C1 (рис.
16). Докажем, что △ABC = △A1B1C1. Действительно по теореме Пифагора AC = AB2 − BC2 = A1B12 − B1C12 = A1C1. Тогда треуголь-
ники ABC и A1B1C1 равны по третьему признаку равенства.
Теорема 1.6.2 (Свойство). Гипотенуза прямоугольного треугольника вдвое больше медианы, прове- денной из вершины прямого угла.
√√
![]()
![]()
14
Доказательство.
Рис. 17. Теорема 1.6.2.
Рассмотрим прямоугольный треугольник ABC, с прямым углом C и медианой CM (тогда AM = MB). Докажем, что 2 ⋅ CM = AB.
Первый способ.
Предположим, что это не так. Тогда CM ≠ MA, и, следовательно, ∠MCA ≠ ∠A (рис. 17). Тогда выберем на гипотенузе AB такую точку M1, что ∠M1CA = ∠A (это возможно по аксиоме 2). Тогда △M1CA – равнобедренный. Кроме того ∠B = 90○ − ∠A = 90○ − ∠M1CA = ∠M1CB, то есть треугольник M1CB – равнобедренный, и M1C = M1B. Но тогда M1B = M1A, то есть M1 – середина гипотенузы AB, что невозможно.
Рис. 18. Теорема 1.6.2.
Второй способ.
Достроим треугольник ABC до прямоугольника ABCD (рис. 18). Диагонали AB и CD равны и точкой пересечения M делятся пополам. Следовательно, 2CM = CD = AB.
Теорема 1.6.3 (Признак). Если медиана треугольника равна половине стороны, к которой она про- ведена, то треугольник прямоугольный.
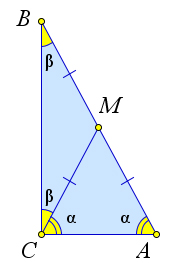
Рис. 19. Теорема 1.6.3.
15
Доказательство.
Рассмотрим треугольник ABC, в котором MC – медиана, и MC = MA = MB. Докажем, что тогда ABC – прямоугольный. Действительно, △MCA и △BMC – равнобедренные, следовательно, ∠A = ∠MCA = α и ∠B = ∠BCM = β. Тогда 2α + 2β = 180○. Откуда получаем, что ∠C = α + β = 90○.
1.6.2 Прямоугольный треугольник с углом в 30○ Теорема 1.6.4 (Свойство). Катет прямоугольного треугольника, лежащий напротив угла в 30○,
равен половине гипотенузы.
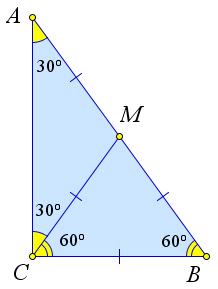
Доказательство.
Рис. 20. Теорема 1.6.4.
Рассмотрим треугольник ABC, в котором ∠C = 90○, ∠A = 30○. Докажем, что AB = 2 ⋅ CB (рис.
20). Пусть CM – медиана. Тогда по теореме 1.6.2 CM = MA = MB, следовательно, △AMC и △BMC
– равнобедренные. Тогда ∠A = ∠ACM, следовательно, ∠MCB = 90∠BCM = 60○. Тогда △BCM –
равносторонний, следовательно, BC = BM = 1 ⋅ AB. 2
Теорема 1.6.5 (Первый признак). Если катет прямоугольного треугольника равен половине гипо- тенузы, то угол, противолежащий этому катету, равен 30○.
Доказательство.
![]()
Рассмотрим прямоугольный треугольник ABC, в котором ∠C = 90○, BC = 1 ⋅AB (рис. 20). Докажем,
2
что ∠A = 30○. Теорема 1.6.6 (Второй признак). Если в треугольнике напротив угла в 30○ лежит сторона, равная
половине другой стороны этого треугольника, то треугольник прямоугольный.
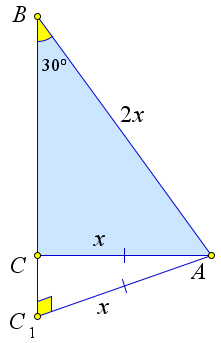
Доказательство.
Первый способ.
Рис. 21. Теорема 1.6.6.
16
Рассмотрим треугольник ABC, в котором AC = x, AB = 2x, ∠B = 30○ (рис. 21). Докажем, что тогда ∠C = 90○.
Предположим противное, тогда из точки B можно опустить перпендикуляр AC1 на прямую CB. Треугольник ABC1 – прямоугольный,∠B = 30○, следовательно, AC1 = x. Тогда △CAC1 – равнобедрен- ный, и ∠C1 = ∠ACC1 = 90○, что невозможно. Значит, ∠C = 90○.
Рис. 22. Теорема 1.6.6.
Второй способ. Рассмотрим треугольник ABC, в котором AC = x, AB = 2x, ∠B = 30○ (рис. 22). По теореме синусов
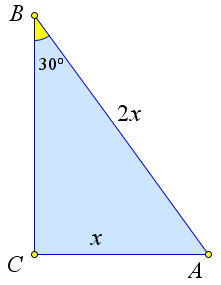
для △ABC: откуда sin∠C = 1, то есть ∠C = 90○.
x = 2x , sin 30○ sin ∠C
![]()
![]()
2 Многоугольники. Четырехугольники
2.1 Многоуольники
Теорема 2.1.1 (Свойства). У каждого многоугольника есть углы, меньшие 180○. Теорема 2.1.2 (Свойства выпуклого многоугольника).
1○ У выпуклого многоугольника все углы меньше 180○. 2○ Отрезок, соединяющий любые две точки выпуклого многоугольника (в частности, любая его
диагональ), содержится в этом многоугольнике. Теорема 2.1.3. Сумма углов выпуклого n-угольника равна 180○(n − 2).
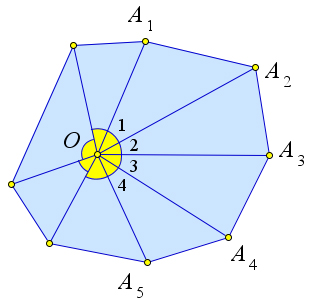
Рис. 23. Теорема 2.1.3.
Доказательство.
Рассмотрим n-угольник A1A2A3 ...An. Возьмём внутри этого многоугольника произвольную точку O. Сумма углов всех треугольников A1OA2, A2OA3, A3OA4, ..., An−1OAn равна 180○ ⋅n. C другой стороны эта сумма складывается из суммы всех внутренних углов многоугольника и полного угла ∠O=∠1+∠2+∠3+...=30○.Тогдасуммаугловрассматриваемогоn-угольникаравна180○⋅n−360○ = 180○ ⋅ (n − 2).
17
Следствие 2.1.3.1. Сумма углов невыпуклого n-угольника равна 180○(n − 2).
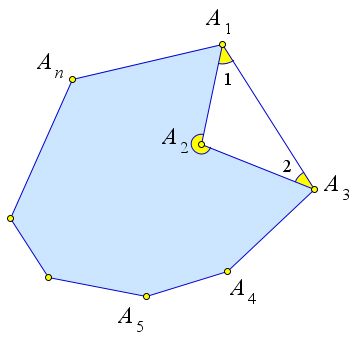
Доказательство.
Рис. 24. Теорема 2.1.3.1.
Рассмотрим многоугольник A1A2 ...An, у которого только угол ∠A2 невыпуклый, то есть ∠A2 > 180○. Обозначим сумму его улов S. Соединим точки A1A3 и рассмотрим многоугольник A1A3 ...An. Сумма углов этого многоугольника равна 180○⋅(n−1−2) = S−∠A2+∠1+∠2 = S−∠A2+180○−∠A1A2A3 = S+180○−(∠A1A2A3+∠A2)=S+180○−360○.Следовательно,S=180○⋅(n−1−2)+180○ =180○⋅(n−2).
Если у исходного многоугольника более одного невыпуклого угла, то описанную выше операцию можно проделать с каждым таким углом, что и приведет к доказываемому утверждению.
Утверждение 2.1.4. Сумма внешних углов n-угольника равна 360○.
Рис. 25. Теорема 2.1.4.
Доказательство.
Внешний угол при вершине A1 равен 180○ −∠A1 (рис. 25). Сумма всех внешних углов равна ∑(180○ −
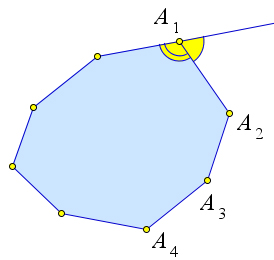
∠An)=n⋅180○ −∑An =n⋅180○ −180○ ⋅(n−2)=360○. n
n
Теорема 2.1.5. Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.
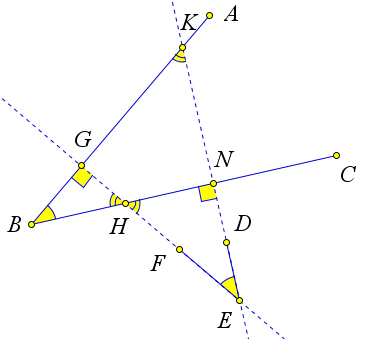
Рис. 26. Теорема 2.1.5.
Доказательство.
Рассмотрим острые углы ∠ABC и ∠DEF, у которых DE ⊥ BC, FE ⊥ BA (рис. 26). Обозначим точки пересечения: FE∩BC =H,FE∩BA=G,ED∩BC =N,ED∩BA=K. Тогда ∠N =∠G=90○. Из треугольников △BKN и △GKE: ∠B = 90○ − ∠K = ∠E.
18
Если же оба угла тупые, то они равны, так как по доказанному равны смежные с ними острые углы.
2.2 Четырехугольники
2.2.1 Параллелограмм Определение 2.1. Параллелограммом называется четырехугольник, у которого противоположные
стороны попарно параллельны.
Рис. 27. Определение 2.1.
Теорема 2.2.1 (Свойства параллелограмма). 1○ В параллелограмме противоположные стороны равны и противоположные углы равны. 2○ Диагонали параллелограмма точкой пересечения делятся пополам. 3○ Диагональ параллелограмма делит его на два равных треугольника. 4○ Сумма углов параллелограмма, прилежащих к одной стороне, равна 180○.
Доказательство.
Рис. 28. Теорема 2.2.1.
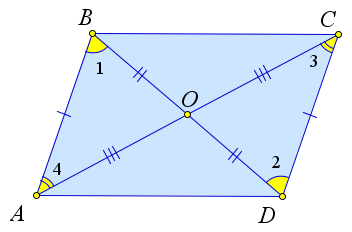
Докажем первый пункт теоремы. Проведем в параллелограмме ABCD диагональ AC (рис. 28). По определению параллелограмма AB ∥ CD и BC ∥ AD, следовательно, ∠1 = ∠2,∠3 = ∠4. Тогда треугольники ABC и ADC равны по второму признаку равенства (AC – общая), следовательно AB = CD, BC = AD. Итак, первый и третий пункты теоремы доказаны.
Рис. 29. Теорема 2.2.1.
Докажем второй пункт теоремы. Пусть диагонали AC и BD параллелограмма ABCD пересекаются в точке O (рис. 29). По определению параллелограмма AB ∥ CD, следовательно, ∠1 = ∠2, ∠3 = ∠4, как накрест лежащие. Кроме того AB = CD по первому пункту теоремы, следовательно, △ABO = △CDO. Из равенства этих треугольников следует, что AO = OC и BO = OD.
Докажем четвертый пункт теоремы. ∠A + ∠B = 180○, так как это односторонние углы при парал- лельных прямых BC и AD (рис. 27).
19
Теорема 2.2.2 (Признаки параллелограмма).
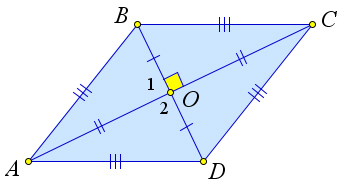
Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник – параллелограмм.
Если две противоположные стороны четырехугольника равны и параллельны, то этот четы- рехугольник параллелограмм.
Если диагонали четырехугольника делятся точкой пересечения пополам, то этот четырех- угольник – параллелограмм.
Если противоположные углы четырехугольника попарно равны, то этот четырехугольник – параллелограмм.
Доказательство.
Докажем первый пункт теоремы.
Рассмотрим четырехугольник ABCD, в котором AB = CD, BC = AD (рис. 28). Докажем, что ABCD – параллелограмм.
Проведем диагональ AC. Треугольники △ACB и △ACD равны по третьему признаку равенства, следовательно ∠3 = ∠4. Но так как эти углы являются накрест лежащими при прямых AB и CD и секущей AC, то AB ∥ CD. Аналогично ∠1∠2, и следовательно BC ∥ AD. А значит, ABCD – паралле- лограмм по определению.
Докажем второй пункт теоремы.
Рассмотрим четырехугольник ABCD, в котором AB = CD и AB ∥ CD (рис. 28). Докажем, что тогда ABCD – параллелограмм.
Проведем диагональ AC. Треугольники △ACB и △ACD равны по второму признаку равенства (AB = CD, AC – общая, ∠3 = ∠4, как накрест лежащие). Следовательно, BC = AD. Тогда ABCD – параллелограмм по первому пункту теоремы.
Докажем третий пункт теоремы.
Рассмотрим четырехугольник ABCD, в котором диагонали AC и BD пересекаются в точке O, и при этом AO = OC, BO = OD (рис. 29). Докажем, что ABCD – параллелограмм.
Действительно, ∠1 = ∠2,∠3 = ∠4, как вертикальные, следовательно, △AOB = △COD,△BOC = △AOD по второму признаку равенства. Тогда AB = CD и BC = AD, и, следовательно, ABCD – параллелограмм по первому пункту теоремы.
Докажем четвертый пункт теоремы.
2.2.2 Прямоугольник Определение 2.2.
1. Прямоугольник - это параллелограмм с прямым углом.
2. Прямоугольник - это четырехугольник, у которого все углы прямые.
Замечание. Пункты 1 и 2 определения 2.2 эквивалентны.
Доказательство.
Действительно, если в параллелограмме есть один прямой угол, то все остальные его углы тоже прямые (так как противоположные стороны параллельны).
Обратно, если в четырехугольнике все углы прямые, то его противоположные стороны параллель- ны, и, следовательно, это параллелограмм.
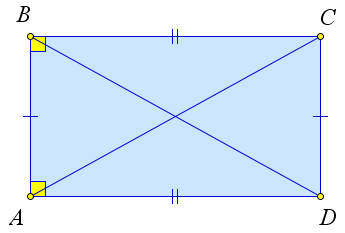
Теорема 2.2.3 (Свойство прямоугольника). Диагонали прямоугольника равны.
Рис. 30. Теорема 2.2.3.
20
Доказательство.
Рассмотрим прямоугольник ABCD. Докажем, что AC = BD (рис. 30).
Поскольку прямоугольник – это частный случай параллелограмма ,то BC = AD. Тогда треуголь- ники △ABC и △DAB равны по первому признаку (BC = AD, AB – общая, ∠A = ∠B = 90○). Следова- тельно, AC = BD.
Теорема 2.2.4 (Признак прямоугольника). Если в параллелограмме диагонали равны, то этот па- раллелограмм – прямоугольник.
Доказательство.
Рассмотрим параллелограмм ABCD, в котором AC = BD (рис. 30). Докажем, что этот параллело- грамм – прямоугольник.
Действительно, треугольники △ABC и △DAB равны по третьему признаку (BC = AD, AC = BD, AB – общая). Тогда ∠A = ∠B. Но поскольку ∠A + ∠B = 180○, то ∠A = ∠B = 90○.
2.2.3 Ромб Определение 2.3. Ромб – это четырехугольник, у которого все стороны равны. Теорема 2.2.5 (Свойства ромба).
1○ Диагонали ромба взаимно перпендикулярны. 2○ Диагонали ромба являются биссектрисами его углов.
Рис. 31. Теорема 2.2.5.
Доказательство.
Рассмотрим ромб ABCD, в котором диагонали AC и BD пересекаются в точке O. Докажем, что они перпендикулярны и являются биссектрисами углов ромба.
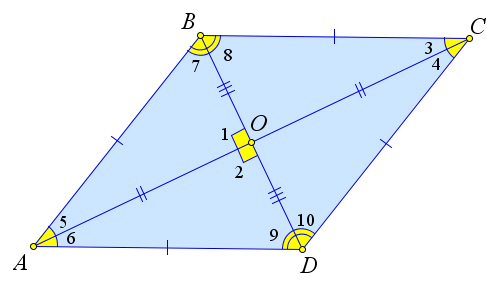
Действительно, так как ABCD – частный случай параллелограмма, то диагонали точкой пере- сечения делятся пополам, то есть AO = OC,BO = OD. Тогда, так как AB = BC = CD = DA, то △AOB = △BOC = △COD = △AOD по третьему признаку равенства. Тогда ∠1 = ∠2 = 90○, так как это смежные углы. Кроме того, ∠3 = ∠4 = ∠5 = ∠6, ∠7 = ∠8 = ∠9 = ∠10. Таким образом диагонали перпендикулярны и являются биссектрисами углов ромба.
Теорема 2.2.6 (Признаки ромба).
Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм – ромб.
Если одна из диагоналей параллелограмма является биссектрисой его угла, то этот паралле- лограмм – ромб.
Если диагональ выпуклого четырехугольника является биссектрисой двух его углов, то такой четырехугольник – ромб.
21
Доказательство.
a)
b)
Рис. 32. Теорема 2.2.6.
Докажем первый пункт теоремы. Рассмотрим параллелограмм ABCD, в котором AC ⊥ BD (рис. 32 a). Докажем, что ABCD – ромб. В параллелограмме диагонали точкой пересечения делятся пополам, следовательно, AO = OC, BO =
OD. Кроме того, ∠1 = ∠2 = 90○. Тогда △AOB = △AOD по первому признаку равенства. Следовательно AB = AD. А так как ABCD – параллелограмм, то BC = AD = AB = CD, то есть ABCD – ромб.
Докажем второй пункт теоремы.
Рассмотрим параллелограмм ABCD, в котором диагональ AC является биссектрисой угла ∠A, то есть ∠1 = ∠2 (рис. 32 b). Докажем, что ABCD – ромб.
∠2 = ∠3, как накрест лежащие, следовательно, ∠1 = ∠3, то есть △ABC – равнобедренный и AB = BC. А так как ABCD – параллелограмм, то AB = CD,BC = AD, то есть AB = BC = CD = AD, и ABCD – ромб.
2.2.4 Квадрат Определение 2.4.
1. Квадрат – это ромб с прямым углом.
2. Квадрат – это прямоугольник, у которого все стороны равны.
Замечание. Пункты 1 и 2 определения 2.4 эквивалентны.
Доказательство.
Действительно, если в ромбе есть один прямой угол, то и все остальные углы ромба прямые, то есть это прямоугольник, у которого все стороны равны.
Обратно, если в прямоугольнике все стороны равны, то это ромб с прямым углом. Теорема 2.2.7 (Свойства квадрата).
1○ Все углы квадрата прямые.
2○ Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и являются биссектрисами его углов.
Доказательство.
Оба пункта теоремы являются очевидными следствиями определения 2.4 Теорема 2.2.8 (Признак квадрата). Если диагонали прямоугольника взаимно перпендикулярны, то
этот прямоугольник - квадрат.
Доказательство.
Действительно, если в прямоугольнике диагонали перпендикулярны, то это ромб, а следовательно, и квадрат.
2.2.5 Трапеция
Определение 2.5. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны (рис. 33).
22
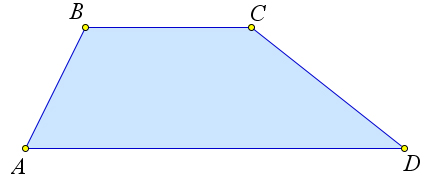

a)
Рис. 33. Определение 2.5. Замечание. Сумма углов при боковой стороне трапеции равна 180○.
Доказательство.
b)
Действительно, так как основания трапеции параллельны, а боковая сторона является секущей, то углы при боковой стороне являются внутренними односторонними углами при параллельных прямых, и, следовательно, их сумма равна 180○.
Теорема 2.2.9. Два треугольника, образованные боковыми сторонами трапеции и отрезками ее диагоналей, равны по площади.
Замечание. Эту теорему можно доказать только после доказательства теоремы 3.2.3.
Рис. 34. Теорема 2.2.9.
Доказательство.
Рассмотрим трапецию ABCD, у которой диагонали AC и BD пересекаются в точке O (рис. 34). Докажем, что S△AOB = S△COD.
Рассмотрим треугольники △ABD и △ACD. У этих треугольников общее основание AD, кроме того их высоты, проведенные к стороне AD из точек B и C соответственно, тоже равны. Следовательно,
S△ABD = S△ACD. Но тогда S△AOB = S△ABD − S△AOD = S△ACD − S△AOD = S△COD. Определение 2.6.
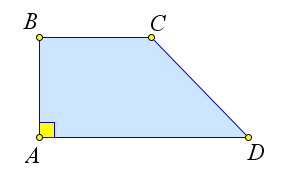
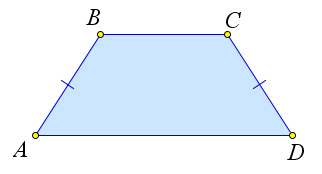
1. Трапеция называется равнобедренной, если ее боковые стороны равны (рис. 35 a). 2. Трапеция называется прямоугольной, если один из ее углов равен 90○ (рис. 35 b).
a)
b)
Теорема 2.2.10 (Свойства равнобедренной трапеции).
1○ Углы при основании равнобедренной трапеции равны.
2○ Диагонали равнобедренной трапеции равны.
Рис. 35. Определение 2.6.
3○ Диагонали равнобедренной трапеции, пересекаясь, образуют два равных и два равнобедренных треугольника.
23
4○ Проекция боковой стороны равнобедренной трапеции на основание равна полуразности основа- ний, а проекция диагонали – полусумме оснований.

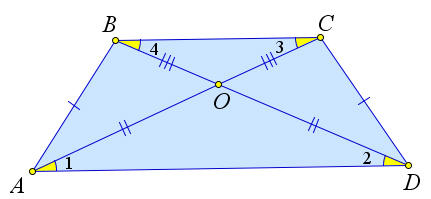
a) b) Рис. 36. Теорема 2.2.10.
Доказательство.
с)
Докажем первый пункт теоремы. Рассмотрим равнобедренную трапецию ABCD, AB = CD (рис. 36 a). Докажем, что ∠A = ∠D. Проведем из точек B и C высоты BE и CF. Треугольники △ABE и △CFD равны по катету и
гипотенузе (AB = CD, BE = CF ). Следовательно, ∠A = ∠D. Докажем второй пункт теоремы. В равнобедренной трапеции ABCD рассмотрим треугольники △ABD и △ACD (рис. 36 b). Они
равны по первому признаку (AB = CD, AD – общая, ∠A = ∠D по первому пункту). Следовательно, AC = BD.
Докажем третий пункт теоремы.
Докажем третий пункт теоремы. Пусть диагонали равнобедренной трапеции ABCD пересекаются в точке O (рис. 36 с). Докажем, что треугольники △AOD и BOC – равнобедренные, а треугольники △AOB и △COD равны.
Действительно, во втором пункте уже было доказано, что △ABD = △ACD, следовательно, ∠1 = ∠2, а так как они накрест лежащие с углами ∠3 и ∠4 соответственно, то ∠3 = ∠4, что и означает, что треугольники △AOD и BOC – равнобедренные. Тогда AO = OD и BO = OC, и как следствие, △AOB = △COD по третьему признаку равенства треугольников.
Докажем четвертый пункт теоремы.
Так как △AEB = △CFD (по катету и гипотенузе), то AE = FD (рис. 36 a). Кроме того, EF = BC, следовательно, AE = AD−BC и AF = AD−BC + BC = AD+BC .
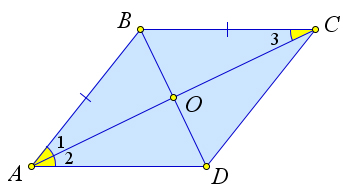
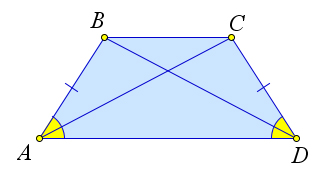
Теорема 2.2.11 (Признаки равнобедренной трапеции). 1. Если углы при основании трапеции равны, то она равнобедренная. 2. Если диагонали трапеции равны, то она равнобедренная.
![]()
222
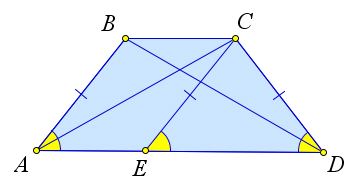
Доказательство.
Докажем первый пункт теоремы.
a)
b)
Рис. 37. Теорема 2.2.12.
Рассмотрим трапецию ABCD, в которой ∠A = ∠D (рис. 37 a). Докажем, что тогда AB = CD, то есть трапеция равнобедренная.
Проведем из вершины C отрезок CE параллельный стороне AB. Тогда ∠A = ∠CED, как соответ- ственные углы. Следовательно, ∠CED = ∠D, а тогда △CED – равнобедренный. А поскольку AB = CE (ABCE – параллелограмм), то AB = CD.
Докажем второй пункт теоремы.
24
Рассмотрим трапецию ABCD, у которой AC = BD (рис. 37 b). Докажем, что тогда AB = CD.
Возьмем на прямой AD точки E и F так, чтобы CF ∥ BD, BE ∥ CA. Тогда AEBC и BCFD - параллелограммы, так как их противоположные стороны попарно параллельны. Следовательно, BC = EA = DF и EB = BD = CA = CF. Тогда треугольники EBD и ACD равны по третьему признаку (ED = EA + AD = DF + AD = AF ). Кроме того, эти треугольники равнобедренные, следовательно, ∠1 = ∠2 = ∠4 = ∠5. А так как BC ∥ AD, то ∠6 = ∠5 и ∠1 = ∠3, как накрест лежащие. Тогда треугольники BOC и AOD равнобедренные, следовательно BO = OB, AO = OD. Тогда △AOB = △COD по первому признаку равенства (∠BOC = ∠COD, как вертикальные). Следовательно, AB = CD.
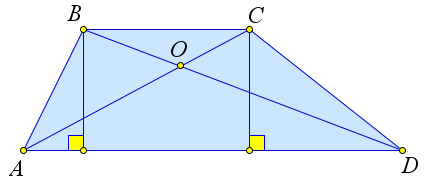
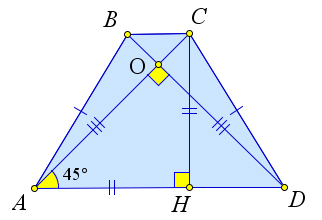
Теорема 2.2.12. В равнобедренной трапеции со взаимно перпендикулярными диагоналями высота равна средней линии.
Рис. 38. Теорема 2.2.12.
Доказательство.
Рассмотрим равнобедренную трапецию ABCD, в которой AC ⊥ BD. Докажем, что в такой трапеции высота CH равна средней линии то есть полусумме оснований (рис. 38).
Действительно, △AOD – равнобедренный и прямоугольный, следовательно, ∠AOD = 45○. Тогда △AHC – равнобедренный, то есть AH = CH. Но отрезок CH равен полусумме оснований по пункту 4 теоремы 2.2.10.
2.3 Средняя линия треугольника и трапеции. Теорема Фалеса
Определение 2.7. Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Теорема 2.3.1 (Свойства средней линии треугольника). Средняя линия треугольника параллельна стороне треугольника и равна ее половине.
Рис. 39. Теорема 2.3.1.
Доказательство.
Рассмотрим △ABC, с основанием AC и средней линией MN (рис. 39). Докажем, что MN ∥ AC и MN = 1 ⋅AC.
2
На прямой M N за точкой N выберем точку D так, чтобы выполнялось M N = N D. Тогда △BMN = △NDC по первому признаку равенства (BN = NC,MN = ND, ∠BNM = ∠DNC). Тогда ∠1 = ∠2, следовательно, AB ∥ DC. Кроме того, из равенства треугольников следует, что MB = DC. Но MB = MA, следовательно MA = DC. Тогда AMDC – параллелограмм (MB = MA, MA ∥ DC). Следовательно,MD∥AC иAC=MD=2⋅MN.
Теорема 2.3.2 (Признаки средней линии треугольника). 1. Если в треугольнике ABC точка M – середина стороны BC, а точка N принадлежит стороне
AB, и при этом MN ∥ AC, то MN – средняя линия. 25
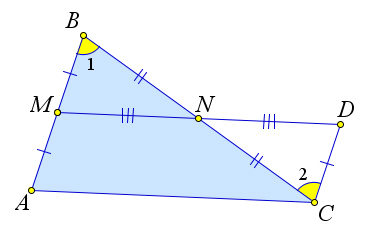
2. Если в треугольнике ABC точки M и N принадлежат сторонам BC и AB соответственно, при этом MN ∥ AC и 2∣MN∣ = ∣AC∣, то MN – средняя линия.
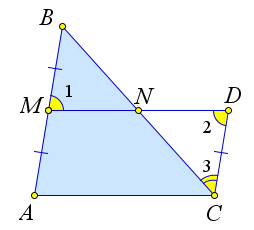
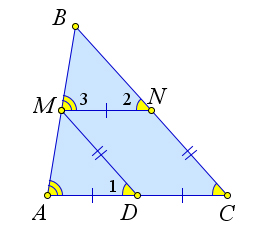
Доказательство.
Докажем первый пункт теоремы.
a)
b)
Рис. 40. Теорема 2.3.2.
Рассмотрим △ABC, в котором M – середина AB, N лежит на стороне BC, MN ∥ AC (рис. 40 a). Докажем, что MN – средняя линия.
Выберем на прямой MN за точкой N такую точку D, что MD = AC. Тогда AMDC – паралле- лограмм (AC = MD, AC ∥ MD). Следовательно, ∠B = ∠3,∠1 = ∠2, так как AM ∥ CD. Кроме того AM = DC, как противоположные стороны параллелограмма. Следовательно BM = MA = DC. Тогда △BMN = △NDC по второму признаку равенства. Следовательно, BN = NC, то есть MN – средняя линия.
Докажем второй пункт теоремы.
Рассмотрим треугольник ABC, в котором на сторонах AB и BC взяты точки M и N соответственно так, что MN ∥ AC и 2 ⋅ MN = AC (рис. 40 b). Докажем, что тогда MN – средняя линия треугольника ABC.
Пусть D – это середина AC. Тогда MNDC – параллелограмм (MN = DC, MN ∥ DC). Следо- вательно, MD ∥ NC. Тогда ∠1 = ∠C = ∠2, как соответственные при параллельных прямых. Кроме того ∠A = ∠3. Следовательно, △BMN = △AMD по второму признаку равенства. Тогда BM = MA и BN = MD = NC, то есть MN – средняя линия △ABC.
Теорема 2.3.3 (Теорема о параллелограмме Вариньона). Середины сторон произвольного четырех- угольника являются вершинами параллелограмма.

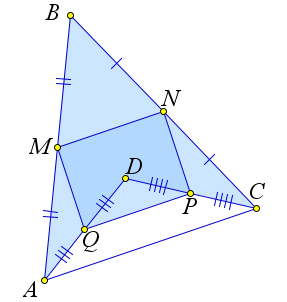
Доказательство.
a)
b)
Рис. 41. Теорема 2.3.3.
Рассмотрим произвольный четырехугольник ABCD, в котором точки M,N,P и Q являются сере- динами сторон AB,BC,CD и AD соответственно. Докажем, что MNPQ – параллелограмм (рис. 41 a).
Действительно, MN – средняя линия треугольника ABC, а QP – средняя линия треугольника ADC. Следовательно MN ∥ AC ∥ QP и MN = 1 ⋅ AC = QP. Тогда MNPQ - параллелограмм по
2
первому признаку. Доказательство не изменяется, если ABCD – невыпуклый четырехугольник (рис. 41 b).
26
Теорема 2.3.4 (Теорема Фалеса). Если на одной из двух прямых отложить последовательно несколько равных отрезков, а потом через их концы провести параллельные прямые, то они отсекут на другой прямой равные отрезки.
Доказательство.
a)
Рис. 42. Теорема 2.3.4.
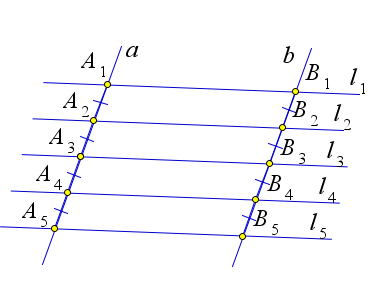
Пусть параллельные прямые l1,l2,l3 пересекают прямые a и b в точках A1,A2,A3 и B1,B2,B3 со- ответственно. Пусть при этом A1A2 = A2A3. Докажем, что тогда B1B2 = B2B3.
Рассмотрим случай, когда прямые a и b параллельны (рис. 42 a).
Тогда A2A1B1B2 и A3A2B2B3 – параллелограммы, следовательно, A1A2 = B1B2 и A2A3 = B2B3, и так как A1A2 = A2A3, то B1B2 = B2B3.
Рассмотрим случай, когда прямые a и b не параллельны (рис. 42 b).
Проведем через точку B1 прямую c, параллельную прямой a. Пусть прямые l2 , l3 , l4 и прямая c пересекаются в точках C2, C3, C4. По первому случаю B1C2 = C2C3, кроме того B2C2 ∥ B3C3. Тогда по первому пункту теоремы 2.3.2 B2C2 – средняя линия, то есть B1B2 = B2B3.
Замечание. Утверждение обратное теореме Фалеса неверно. То есть, из того, что прямые прямые l1,l2,l3 пересекают прямые a и b в точках A1,A2,A3 и B1,B2,B3 соответственно, и при этом A1A2 = A2A3 и B1B2 = B2B3, не следует, что прямые l1,l2 и l3 параллельны (рис. 43).
Рис. 43. Замечание к теореме фалеса. Определение 2.8. Отрезок, соединяющий середины боковых сторон трапеции, называется средней
линией трапеции.
Теорема 2.3.5 (Свойства средней линии трапеции). Средняя линия трапеции параллельна основани- ям трапеции и равна их полусумме.
Рис. 44. Теорема 2.3.5.
b)
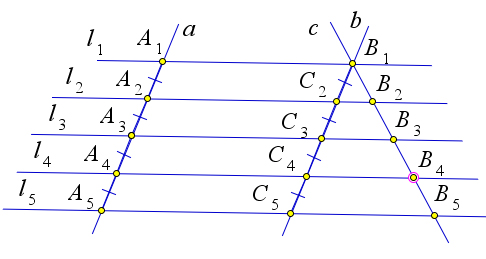
27
Доказательство.
Рассмотрим трапецию ABCD, в которой проведена средняя линия MN. Докажем, что MN ∥ AD и M N = AD+BC (рис. 44).
2
Проведем через точку M прямую FE параллельно CD (F ∈ CB,E ∈ AD). Тогда CDEF – паралле- лограмм (F C ∥ ED, F E ∥ CD). Следовательно, F E = CD.
Кроме того △FBM = △AME, по второму признаку равенства (∠1 = ∠2, как накрест лежащие, ∠3 = ∠4, как вертикальные, AM = MB, так как M – середина). Следовательно, FM = ME. Тогда FMNC и MNDE - параллелограммы (FM = ME = ND = NC и FE ∥ CD). Следовательно, MN ∥ BC.
Кроме того из равенства треугольников △FBM = △AME следует,что FB = AE. Тогда MN = FC = FB+BC=2FB+2BC =(FB+AE)+(BC+ED) =BC+AD.
222
Теорема 2.3.6 (Признаки средней линии трапеции). 1. Пусть отрезок MN соединяет точки на боковых сторонах трапеции. Если M – середина боко-
вой стороны, и MN параллелен основаниям трапеции, то MN – это средняя линия трапеции. 2. Пусть отрезок MN соединяет точки на боковых сторонах трапеции. Если MN параллелен
основанием трапеции и равен их полусумме, то MN – средняя линия трапеции.
Рис. 45. Теорема 2.3.6.
Доказательство.
Первый пункт теоремы является прямым следствием теоремы Фалеса. Докажем второй пункт теоремы. Рассмотрим трапецию ABCD, в которой на боковых сторонах AB и CD выбраны точки M и N
соответственно, и при этом MN = AD+BC (рис. 45). Докажем, что тогда MN – средняя линия трапеции
2
ABCD. Предположим противное, то есть MN – не средняя линия данной трапеции. Если ровно одна из точек M или N является серединой, то по первому пункту теоремы MN – это
средняя линия, так как MN параллельна основаниям трапеции. Пусть точки M и N – не середины боковых сторон. Тогда пусть M′N′ – средняя линия трапеции.
![]()
![]()
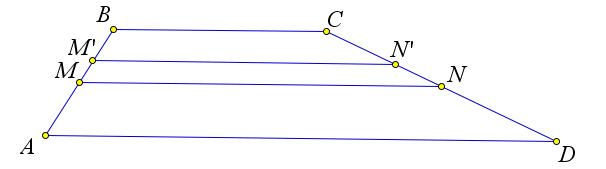
Следовательно, M′N′ = BC+AD = MN и MN ∥ BC ∥ MN. Но тогда MNN′M′ – параллелограмм, и, 2
следовательно, MM′ ∥ NN′, что противоречит тому, что ABCD – это трапеция. Следовательно, MN – средняя линия.
Теорема 2.3.7. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности ее осно- ваний.
Рис. 46. Теорема 2.3.7.
Доказательство.
Рассмотрим трапецию ABCD, в которой точки E и F – это середины диагоналей AC и BD соот- ветственно (рис. 46). Докажем, что EF = AD−BC .
2
По теореме Фалеса точки средняя линия трапеции MN делит диагонали AC и BD пополам, то есть
точки E и F лежат на средней линии. Тогда ME и FN – это средние линии треугольников △ABC и

△DBC. Следовательно, если обозначить BC = 2x, то ME = FN = x. Тогда EF = 2x+AD −x−x = AD−2x =
AD−BC . 2
![]()
22
28
