3. Элементы теории входящего потока. Пуассоновский поток.

Пуассоновским потоком называют ординарный поток заявок с отсутствием последействия, у которых количество заявок, поступающих в систему за промежуток времени t распределено по закону Пуассона:

, t>0, λ>0 (*)

где Р(k,t) - вероятность того, что за время t в систему поступит ровно k заявок

λ - интенсивность потока

Математическое ожидание и дисперсия для закона Пуассона:

М[T]=D[T]=λ*t

Пуассоновский поток может быть как стационарным, так и нестационарным, если

интенсивность является функцией от времени: λ=λ(t).

Простейший поток можно рассматривать как стационарный Пуассоновский поток.

Формула (*) отражает все свойства простейшего потока, если λ не зависит от времени (или если λ константа).

Из формулы (*) видно, что вероятность появления k событий за время t является функцией от k и от t, что характеризует свойство стационарности.

Формула (*) не использует информацию о появлении событий до начала рассматриваемого момента времени, что характеризует свойство отсутствия последействия.

Можно убедиться, что формула (*) отражает и свойство ординарности.

Положив k=0 и 1, найдем соответственно вероятности непоявления событий и появления одного события (заявки).

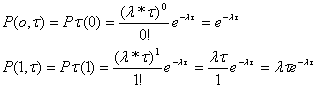
Следовательно, вероятность появления больше чем одного события (заявки) можно найти через противоположное событие.

Воспользуемся разложением в ряд функции

Далее неразборчивый пример

Сравнивая значение Р(1,t) и Р(k>1,t), видно, что при малых значениях t вероятность появления более одного события по сравнению с вероятностью появления одного события пренебрежимо мала, что характеризует свойство ординарности.

Формулу Пуассона можно считать математической моделью простейшего потока событий.

Однако в распределении Пуассона длительности интервалов между

последовательными заявками - это случайные величины с экспоненциальным законом распределения.

Если нестационарный поток, интенсивность которого представляет собой функцию от времени λ=λ(t) описывается законом распределения Пуассона, то такой поток называется Пуассоновским, а не простейшим.

Входящий поток. Для задания входящего потока требований необходимо описать моменты времени их поступления в систему (за­кон поступления) и количество требований, которое поступило одно­временно. Закон поступления может быть детерминированный (на­пример, одно требование поступает каждые 5 мин) или вероятност­ный (требования могут появляться с равной вероятностью в интерва­ле 5±2 мин). В общем случае входящий поток требований описывает­ся распределением вероятностей интервалов времени между сосед­ними требованиями. Часто предполагают, что эти интервалы времени независимые и имеют одинаковое распределение случайных величин, которые образуют стационарный входящий поток требований. Клас­сическая теория массового обслуживания рассматривает так назы­ваемый пуассоновский (простейший) поток требований. Для этого потока число требований k для любого интервала времени распреде­лено по закону Пуассона:

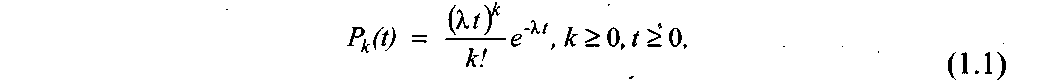
где λ - интенсивность потока требований (число требований за еди­ницу времени). На практике обоснованием того, что входящий поток требова­ний имеет распределение Пуассона, является то, что требования по­ступают от большого числа независимых источников за определен­ный интервал времени. Примерами могут быть вызовы абонентов в телефонной сети, запросы к распределенной базе данных от абонен­тов сети за некоторое время и другие. Для того, чтобы при моделиро­вании задать пуассоновский поток требований в систему, достаточно задать экспоненциальное распределение интервалов времени поступ­ление для соседних требований, графики функций плотности и рас­пределения которых для λ = 1 показаны на рис. 1.1.