
Дополнение:
Регрессионные модели с количественными и качественными переменными
Зачастую в регрессионных моделях в качестве объясняющих переменных приходится использовать не только количественные, но и качественные переменные. Например, спрос на некоторое благо может определяться ценой данного блага, ценой на заменители данного блага, ценой дополняющих благ, доходом потребителей и т. д. (эти показатели определяются количественно). Но спрос может также зависеть от вкусов потребителей, их ожиданий, национальных и религиозных особенностей и т. д. А эти показатели представить в численном виде нельзя. Возникает проблема отражения в модели влияния таких переменных на исследуемую величину. Обычно влияние качественного фактора выражается в виде фиктивной переменной, которая отражает два противоположных состояния качественного фактора. Например, "фактор действует" - "фактор не действует", "курс валюты фиксированный" - "курс валюты плавающий", "сезон летний" - "сезон зимний" и т. д. В этом случае фиктивная переменная может выражаться в двоичной форме. Например, D = 0, если потребитель не имеет высшего образования, D = 1, если потребитель имеет высшее образование; D = 0, если в обществе имеются инфляционные ожидания, D = 1, если инфляционных ожиданий нет.
Такая переменная называется фиктивной (искусственной, двоичной) переменной (индикатором).
Следовательно, кроме моделей, содержащих только количественные объясняющие переменные (обозначаемые Xi), в регрессионном анализе рассматриваются также модели, содержащие лишь качественные переменные (обозначаемые Di), либо и те и другие одновременно.
Например, пусть Y - начальная заработная плата.
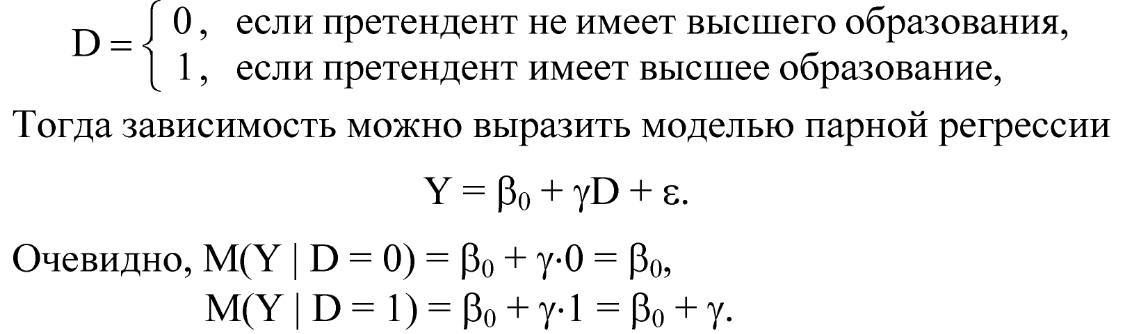
При этом коэффициент βо определяет среднюю начальную заработную плату при отсутствии высшего образования. Коэффициент γ указывает, на какую величину отличаются средние начальные заработные платы при наличии или отсутствии высшего образования у претендента. Проверяя статистическую значимость коэффициента γ с помощью t-статистики либо значимость коэффициента детерминации R2 с помощью F-статистики, можно определить, влияет или нет наличие высшего образования на начальную заработную плату.
Такие модели в экономике крайне редки. Гораздо чаще встречаются модели, содержащие как качественные, так и количественные переменные.
Рассмотрим простейшую модель с одной количественной и одной качественной переменной, имеющей два альтернативных состояния:
![]()
Пусть, например, Y — заработная плата сотрудника фирмы, X -стаж сотрудника, D - пол сотрудника, т. е.
![]()
Тогда ожидаемое значение заработной платы сотрудников при х годах трудового стажа будет:
![]()
![]()
Заработная плата в данном случае является линейной функцией от стажа работы. Причем и для мужчин и для женщин заработная плата меняется с одним и тем же коэффициентом пропорциональности β1. А вот свободные члены в моделях отличаются на величину γ. Проверив с помощью t-статистики статистические значимости коэффициентов β0 и (β0 + γ), можно определить, имеет ли место в фирме дискриминация по половому признаку. Если эти коэффициенты окажутся статистически значимыми, то, очевидно, дискриминация есть. Более того, при γ > 0 — она будет в пользу мужчин, при γ < 0 - в пользу женщин.
Значение качественной переменной, для которого принимается D = 0, называется базовым или сравнительным. Выбор базового значения обычно диктуется целями исследования.
Сравнение двух регрессий (тест Чоу)
В рассматриваемых примерах, предполагалось, что изменение значения качественного фактора влияет лишь на изменение свободного члена. Но это, не всегда так. В частности, предполагалось, что заработная плата сотрудника увеличивается пропорционально стажу с одним и тем же коэффициентом пропорциональности вне зависимости от пола сотрудника, хотя зачастую коэффициент γ1 для сотрудников мужского пола больше аналогичного коэффициента для женщин. Следовательно, необходимо представить, что изменение качественного фактора может привести как к изменению свободного члена уравнения, так и наклона прямой регрессии.
Обычно это характерно для временных рядов экономических данных при изменении институциональных условии, введении новых правовых или налоговых ограничений. Например, можно предположить, что до некоторого года в стране обменный курс был фиксированным, а затем плавающим. Или налог, на ввозимые автомобили был одним, а затем он существенно изменился. В этом случае зависимость может быть выражена следующим образом:
Yt = β0 + β1 Xt + r1Dt + r2DtXt + e,
![]()
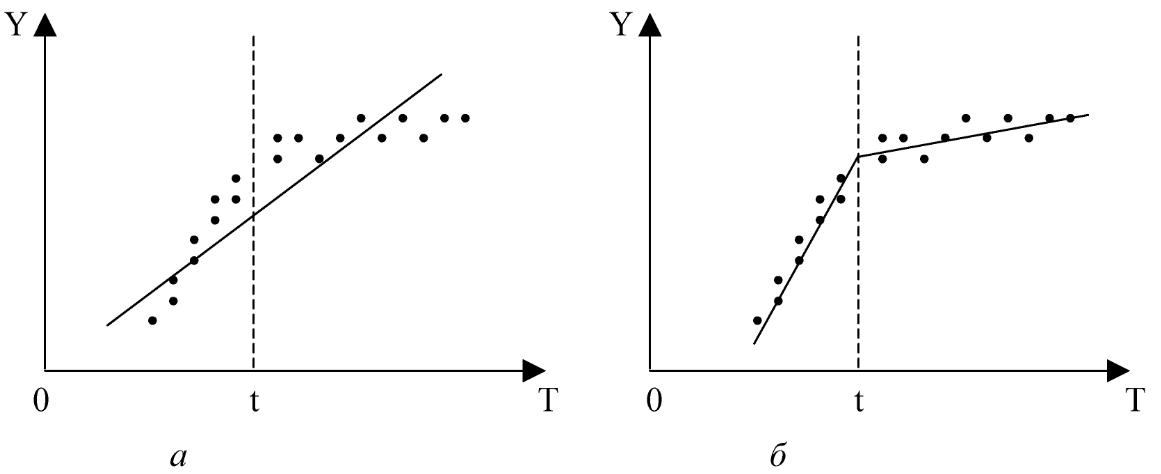
На рис. а зависимость отражается обыкновенной линейной регрессией. На рис. б в модели учитываются изменения, произошедшие с некоторого момента t в характере расположения точек наблюдений. На данном примере хорошо видно, каким образом можно проанализировать, имеет ли смысл разбивать выборку на части и строить для каждой из них уравнение регрессии (т. е. фактически строить сложную регрессию с фиктивными переменными) (рис. б) либо можно ограничиться общей "обыкновенной" регрессией для всех точек наблюдений (рис. а).
Для этого можно использовать тест Чоу, суть которого состоит в следующем.
Пусть имеются две выборки объемами n1 и п2 соответственно. Для каждой из этих выборок оценено уравнение регрессии вида: Y=a0k + a1kX1+a1kX2+ ... +amkXm+ek, k=1,2.
Проверяется нулевая гипотеза о равенстве друг другу соответствующих коэффициентов регрессии
aj1 = aj2 j=0,1,…,m
Другими словами, будет ли уравнение регрессии одним и тем же для обеих выборок?
Пусть суммы Σеik2 (k = 1,2) квадратов отклонений значений уi от линий регрессии равны S1 и S2 соответственно для первого и второго уравнений регрессии.
Пусть по объединенной выборке объема (n1 + n2) оценено еще одно уравнение регрессии, для которого сумма квадратов отклонений уi от уравнения регрессии равна S().
Для проверки гипотезы Н0 в этом случае строится следующая F-статистика:
![]()
Очевидно, F-статистика близка к нулю, если So =S1+ S2 , и это фактически означает, что уравнения регрессии для обеих выборок практически одинаковы. В этом случае F < Fкр. Если же F > Fкр то нулевая гипотеза отклоняется. Приведенные выше рассуждения особенно важны для ответа на вопрос, можно ли за весь рассматриваемый период времени построить единое уравнение регрессии (рис. 6.1, а), или же нужно разбить временной интервал на части и на каждой из них строить свое уравнение регрессии (рис. 6.1, б).
Использование теста Чоу осуществляется достаточно просто. Однако оно менее информативно, нежели общий анализ сложной регрессии с фиктивными переменными, осуществляемый на базе t-статистик, коэффициента детерминации и статистики Дарбина-Уотсона. Однако тест Чоу вполне достаточен, если требуется установить, что зависимости в подвыборках различаются.
