1.2. Условия макроскопического проявления и направление

процессов переноса

Если система находится в состоянии равновесия, то макроскопических проявлений переноса субстанции не наблюдается. Несмотря на тепловое движение молекул, каждая из которых переносит массу, импульс и энергию, макроскопические потоки субстанции при этом отсутствуют вследствие равновероятности переноса в каждом направлении. Конвективный и турбулентный механизмы переноса в условиях равновесия вообще отсутствуют.

Равновесие в однофазной системе устанавливается при равенстве значений в каждой точке пространства макроскопических величин, характеризующих свойства системы: скорости - (x,y,z,t) = const; температуры - T(x,y,z,t) = const; химических потенциалов компонентов - _i(x,y,z,t) = const.

_i характеризует изменение энергии системы при изменении количества частиц сорта i в ней. Химический потенциал компонента может быть выражен через стандартную часть 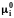и произведение коэффициента активности 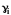на мольную долю соответствующего компонента :

. (1.9)

Для системы, состоящей из двух фаз, условием равновесия является равенство приведенных выше величин в каждой из фаз:

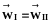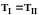, , . (1.10)

Можно выделить отдельно условия гидромеханического, теплового и концентрационного равновесия:

гидромеханическое равновесие : =const; ;

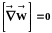тепловое (термическое) равновесие : Т=const; ;

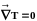концентрационное равновесие : =const, ,

здесь 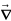- дифференциальный оператор.

Условием проявления процессов переноса и возникновения макроскопических потоков массы, импульса и энергии является неравновесность системы. Направленность процессов переноса определяется самопроизвольным стремлением системы к состоянию равновесия, т.е. процессы переноса приводят к выравниванию скорости, температуры и химических потенциалов компонентов системы. Неоднородности указанных величин являются необходимыми условиями протекания процессов переноса, их называют движущими силами.

Для того чтобы осуществить процесс, необходимо вывести систему из состояния равновесия, т.е. оказать воздействие извне. Это возможно за счет подвода массы или энергии к системе либо действия внешних сил.

1.3. Уравнения переноса

1.3.1. Перенос массы Конвективный механизм. Поток массы в лабораторной системе отсчета за счет конвективного механизма для любой точки системы может быть связан с конвективной скоростью:

, кг/м²с . (1.11)

В случае многокомпонентной среды можно рассмотреть поток массы каждого компонента:

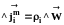, (1.12)

где i - номер компонента, _i - плотность компонента i.

Зачастую удобнее использовать поток вещества, а не массы:

, кмоль/м²с , (1.13)

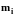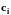где - мольная масса компонента i, кг/кмоль; - мольная концентрация, кмоль/м³. В условиях гидромеханического равновесия конвективная скорость относительно аппарата является нулевой величиной.

Молекулярный механизм. Молекулярный механизм переноса массы можно наблюдать в термодинамически равновесной системе при наличии лишь градиентов концентрации меченых частиц сорта i (i'- изотопы молекул сорта i):

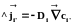. (1.14)

Знак «минус» свидетельствует о противоположной направленности векторов потока вещества и градиента концентрации. Градиент концентрации направлен в сторону максимального увеличения концентрации, а поток вещества - в сторону ее уменьшения, выравнивания неоднородности. Уравнение Энштейна:

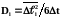. (1.15)

Эти величины называют эйнштейновскими коэффициентами диффузии. Они экспериментально определяются с помощью методов меченых атомов или ядерного магнитного резонанса, а также на основе численного эксперимента методом молекулярной динамики (моделирование движения совокупности частиц на компьютере). 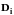зависят от динамических характеристик молекул (масса, потенциал взаимодействия), а также от давления и температуры системы. В газах имеют порядок 10^-6 м²/с, в жидкостях - 10^-9 м²/с, в твердых телах - 10^-12 м²/с, они увеличиваются с ростом температуры и уменьшения давления.

Для изотермической системы в отсутствие турбулентности поток компонента i складывается из диффузионного и конвективного:

, (1.16)

где n - число компонентов в системе. Рассмотрим аппарат, в одной части которого находится компонент 1, а в другой - компонент 2, отделенные друг от друга перегородкой. Давление и температура в обеих частях аппарата одинаковы. Если убрать перегородку, то за счет молекулярной диффузии возникнут противоположно направленные потоки компонентов. Однако величины потоков будут различны вследствие отличия динамических характеристик молекул компонентов и, следовательно, эйнштейновских коэффициентов диффузии . Допустим 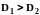, тогда учитывая, что из соотношения Гиббса-Дюгема 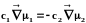, диффузионный поток первого компонента будет больше второго. Молекулярный механизм вызовет суммарный перенос вещества из первой части аппарата во вторую, что приведет к возникновению в закрытом аппарате градиента плотности числа частиц и соответственно давления . А это вызовет противоположно направленный конвективный поток, выравнивающий градиент давления (рис. 1.2).

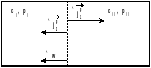
Рис. 1.2. Диффузийные потоки и конвективная скорость, вызванная диффузией в закрытом аппарате

Система отсчета для определения диффузионных потоков задается условием равенства нулю суммарного потока соответствующего признака (обозначим его z_i) в данной системе отсчета:

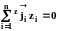. (1.17)

В среднемассовой системе отсчета z_i=m_i (мольная масса компонента), а в среднеобъемной z_i=V_i (парциальный мольный объем компонента V_i, м³/кмоль):

.

Тогда мольный поток компонента i в лабораторной системе отсчета можно представить в виде

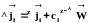, (1.18)

, (1.19)

где - скорость движения соответствующей системы отсчета относительно лабораторной, которая может быть найдена, если измерены экспериментально величины потоков 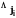. В соответствии с подходом независимой диффузии потоки в системе отсчета z имеют вид

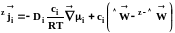, (1.20)

где 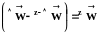- конвективная скорость в системе отсчета z.

Используя дополнительное уравнение (1.17), можно выразить 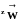через , , 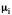, 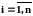и представить потоки в виде

. (1.21)

Выразим химические потенциалы через мольные концентрации, используя соотношение

,

позволяющее сократить на единицу число независимых переменных, можно записать

. (1.22)

В частном случае двухкомпонентной системы матрица вырождается в единственный коэффициент бинарной (взаимной) диффузии :

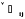
. (1.23)

Это соотношение называется первым законом Фика. Используя подход независимой диффузии, можно выразить коэффициенты взаимной диффузии через эйнштейновские коэффициенты:

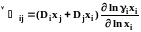. (1.24)

Можно сделать это и для многокомпонентных смесей, связав элементы матрицы 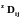с . В среднемассовой системе отсчета коэффициенты бинарной диффузии не обладают свойством симметрии 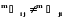и могут быть выражены через :

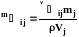(1.25)

При межфазном переносе вещества потоки зачастую записывают относительно границы раздела фаз. Для бинарной смеси, первый компонент которой переходит границу раздела фаз, а второй нет, потоки в одной фазе запишутся в системе отсчета с нулевым потоком второго компонента:

, (1.26)

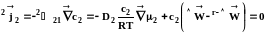. (1.27)

Выразив 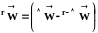из (1.27) и подставив в (1.26), можно получить соотношения для коэффициентов бинарной диффузии в системе отсчета, соответствующей нулевому потоку второго компонента,

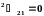; . (1.28)

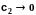
При . Эйнштейновские коэффициенты диффузии не зависят от выбора системы отсчета.

Выражения для макроскопических потоков и коэффициентов переноса:

. (1.29)

Турбулентный механизм. Турбулентный перенос массы можно рассматривать как следствие хаотического перемещения вихрей. Коэффициент турбулентной диффузии зависит как от свойств среды, так и от неоднородности скорости и удаленности от межфазной поверхности. При турбулентном движении суммарный поток вещества относительно лабораторной системы отсчета может быть записан как

(1.30)

или

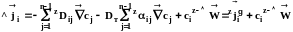, (1.31)

. (1.32)

Для системы отсчета, в которой поток компонента n равен нулю,

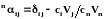, (1.33)

, (1.34)

где 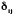- символ Кронекера.

Для двухкомпонентной смеси можно ввести коэффициенты турбулентной диффузии в соответствующей системе отсчета:

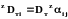. (1.35)

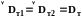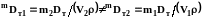Для среднеобъемной системы отсчета , а для среднемассовой . Отношение коэффициентов турбулентной и молекулярной диффузии в пристенной области достигает .